高中数学人教B版必修三:复习—研究函数性质的方法再认识 课件(67张ppt)
文档属性
| 名称 | 高中数学人教B版必修三:复习—研究函数性质的方法再认识 课件(67张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-23 00:22:01 | ||
图片预览








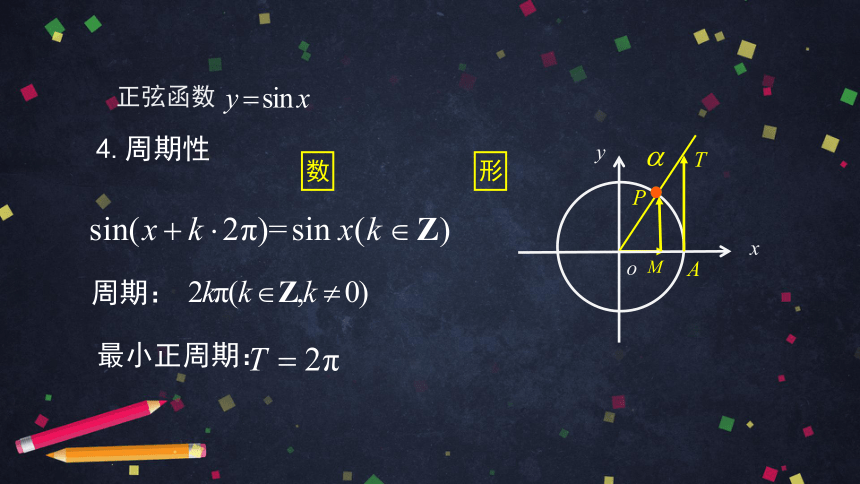
文档简介
(共67张PPT)
复习—研究函数性质的方法再认识
高一年级 数学
问题1. 什么是函数的性质?函数性质一般包括哪些?
函数性质一般包括:定义域、对称性、特殊点(零点)、函数值正负区间、周期性、单调性、最值、值域。
函数性质:函数值 随自变量 变化而变化过程中呈现出的规律性和不变性。
问题2.三角函数性质的研究方法?
从幂、指、对函数到三角函数,函数性质的研究方法是一脉相承的
1.三角函数概念和单位圆直观模型
以正弦函数 性质的研究方法为例
问题2.三角函数性质的研究方法?
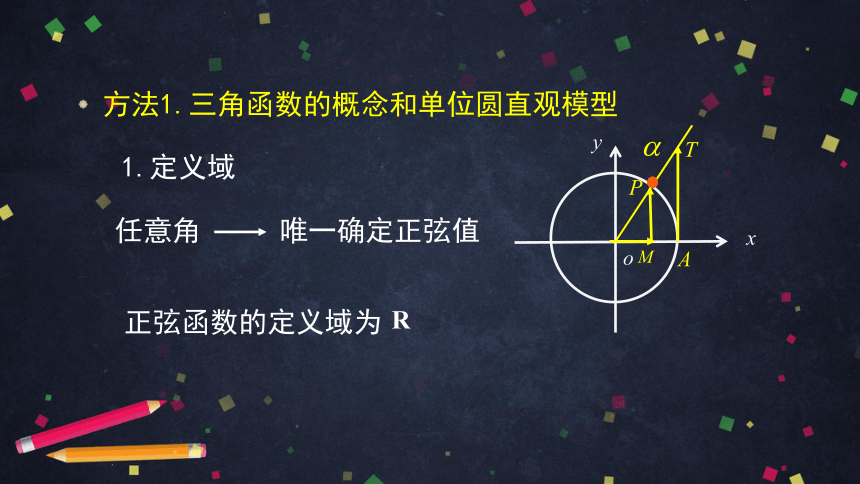
方法1.三角函数的概念和单位圆直观模型
终边与单位圆的交点的
y
o
x
方法1.三角函数的概念和单位圆直观模型
y
o
x
1.定义域
唯一确定正弦值
任意角
正弦函数的定义域为
2.奇偶性
数论证
形观察
正弦函数
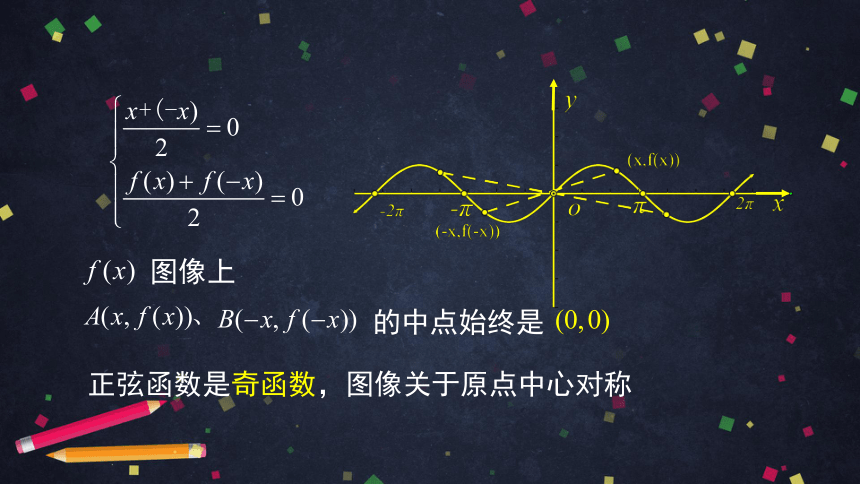
正弦函数是奇函数,图像关于原点中心对称
定义
2.奇偶性
代数特征:
自变量互为相反数时,函数值也互为相反数
数论证
形观察
正弦函数
正弦函数是奇函数,图像关于原点中心对称
的中点始终是
图像上
数
形
3.对称性
正弦函数
代数特征:两个自变量和为 时,对应函数值相等。
3.对称性
正弦函数图像关于直线 轴对称
图像上
,两个点的横坐标
关于 为中点坐标时,对应点的纵坐标相等
周期:
最小正周期:
正弦函数
4.周期性
数
形
y
o
x
正弦函数
5.单调性
数
形
y
o
x
在区间
递增
在区间
递减
y
o
x
正弦函数
5.单调性
6.值域(最值)
当
时,
当
时,
值域:
正弦函数
x
正弦函数的零点是
正弦函数
7.零点
形
数
,角的终边落在 轴上
令
x
方法2.观察三角函数图像
用图像认识和发现性质
1.观察图像,理解性质
图像在研究函数性质中的作用?
2.观察图像,发现新性质
正弦函数的图像是轴对称图形,
对称轴:
观察正弦函数 图像,发现新的对称性
观察到的结果是否准确?
需要代数推理证明
证明:
代数特征:两个自变量和为 时函数值相等
正弦函数的图像是轴对称图形,
对称轴:
梳理研究三角函数性质的方法:
三角函数概念,三角函数单位圆模型,
三角函数运算和推理,三角函数图像。
核心:数形结合
与
的图像
观察函数
两个函数图像关于 轴对称
观察到的结果是否准确?
需要代数推理证明
这种研究函数性质的方法有无体验?
用 代替 中的
得到
解析式:
与
的图像关于 轴对称
求证:
图像上任取一点 ,
则点 关于 轴的对称点
证明:在
图像上任一点 关于
轴的对称点 在 上
与
图像关于 轴对称
同理:
梳理研究函数性质的方法:
函数概念
函数解析式或直观模型
数
形
代数运算和推理
梳理研究函数性质的方法:
核心:数形结合
函数概念
函数解析式或直观模型
数
形
代数运算和推理
观察函数图像,猜想性质
形:
“数” 与“形” 的研究方法特点比较
形象、直观
易于发现
缺少准确性
周期
图像法研究性质的局限性:
不准确、无法全部验证…
数:
形:
严谨,有逻辑
形象、直观
证明有难度
易于发现但缺少准确性
以形助数
由数到形
数形结合
“数” 与“形” 的研究方法特点比较
案例1:已知函数
,研究该函数的性质
转化为熟悉的基本初等函数
追问:分析函数解析式、用代数运算研究函数的性质的优势?
已知函数
,研究该函数的性质
函数性质:定义域、对称性、特殊点(零点)、函数值正负区间、周期性、单调性、最值、值域。
已知函数
,研究该函数的性质
对称轴:
非奇非偶函数
周期:
定义域:
值域:
已知函数
,研究该函数的性质
单调递增区间:
零点:
单调递减区间:
英国数学家詹姆斯?西尔维斯特:
“几何看来有时候要领先于分析,但事实上,几何的先行于分析,只不过像一个仆人走在主人的前面一样,是为主人开路的”
函数性质的研究方法
形
数
数形结合
数学的眼光
数学家华罗庚教授:
数缺形时少直观;
形缺数时难入微。
五点作图法
三角函数图像
图像变换法
描点作图
案例2:三角函数性质帮助做三角函数图像
函数性质
函数性质帮助做三角函数图像
三角函数性质——三角函数图像
在 内取几个特殊值
函数性质帮助做三角函数图像
图像关于直线 对称
得到区间 的图像
函数性质帮助做三角函数图像
图像关于原点 对称
得到区间 的图像
函数性质帮助做三角函数图像
周期是
得到整个定义域 上的图像
函数性质帮助做三角函数图像
(1)求 的值,并说明经过哪些运算得到函数值。
问题3.已知函数
四步运算,
四次对应完成
(2)求 在区间 上的最值
分析(1)
是指谁的范围?
(2)
的自变量是谁?
(3)
正弦直接加工的对象是谁?
问题3.已知函数
令
函数值
自变量
函数值
自变量
问题3.已知函数
(2)求 在区间 上的最值
问题3.已知函数
(2)求 在区间 上的最值
解:
令
问题3.已知函数
(2)求 在区间 上的最值
即 时,
当
取得最大值
即 时,
当
取得最小值
变式:若 在 上恒成立,求 的最小值
问题3.已知函数
若 在 上恒成立,
则
(3)求 的单调递增区间
令
函数值
自变量
函数值
自变量
问题3.已知函数
(3)求 的单调递增区间
让
落在 的增区间内
问题3.已知函数
(3)求 的单调递增区间
的单调增区间是
解:因为
的增区间是
变式1:求函数 在 上的单调递增区间
问题3.已知函数
的增区间是
解:因为
又
,所以
当
时,
当
时,
所以 在 上的单调递增区间是
变式2:若函数 在 上单调递增,求 的最大值
问题3.已知函数
的最大值为
问题3.已知函数
变式2:若函数 在 上单调递增,求 的最大值
的单调增区间是
方法二:
由已知得:
的最大值为
(4)把函数 的图像向左平移 个单位,得到函数 是个奇函数,求 的最小值
问题3.已知函数
因为 是 上的奇函数,所以
解:
因为 是 上的奇函数,所以
时
求函数 的最大值和最小值,以及使函数取得最值时的 的值。
问题4.已知函数
分析:观察函数解析式有何特点?
观察角度:角、次数、名称、结构
思路:化余弦为正弦、统一三角函数名称、角
求函数 的最大值和最小值,以及使函数取得最值时的 的值。
解:
令
问题4.已知函数
求函数 的最大值和最小值,以及使函数取得最值时的 的值。
解:
处于
的增区间
处于
的减区间
问题4.已知函数
求函数 的最大值和最小值,以及使函数取得最值时的 的值。
解:
即
或
时,
即
问题4.已知函数
求函数 的最大值和最小值,以及使函数取得最值时的 的值。
即
时,
当
即
时,
当
问题4.已知函数
求函数 的最大值和最小值,以及使函数取得最值时的 的值。
即
时,
当
问题4.已知函数
研究函数性质的方法再认识:
函数概念
函数解析式或直观模型
数
形
代数运算和推理
观察函数图像,猜想性质
研究函数性质的方法再认识:
以形助数
由数到形
数形结合
函数概念
函数解析式或直观模型
数
形
代数运算和推理
观察函数图像,猜想性质
写一篇小论文:
题目:研究函数性质的方法再认识
作业:
感谢收看
祝同学们学习有怀疑、有思考、
有兴趣、有进步!
复习—研究函数性质的方法再认识
高一年级 数学
问题1. 什么是函数的性质?函数性质一般包括哪些?
函数性质一般包括:定义域、对称性、特殊点(零点)、函数值正负区间、周期性、单调性、最值、值域。
函数性质:函数值 随自变量 变化而变化过程中呈现出的规律性和不变性。
问题2.三角函数性质的研究方法?
从幂、指、对函数到三角函数,函数性质的研究方法是一脉相承的
1.三角函数概念和单位圆直观模型
以正弦函数 性质的研究方法为例
问题2.三角函数性质的研究方法?
方法1.三角函数的概念和单位圆直观模型
终边与单位圆的交点的
y
o
x
方法1.三角函数的概念和单位圆直观模型
y
o
x
1.定义域
唯一确定正弦值
任意角
正弦函数的定义域为
2.奇偶性
数论证
形观察
正弦函数
正弦函数是奇函数,图像关于原点中心对称
定义
2.奇偶性
代数特征:
自变量互为相反数时,函数值也互为相反数
数论证
形观察
正弦函数
正弦函数是奇函数,图像关于原点中心对称
的中点始终是
图像上
数
形
3.对称性
正弦函数
代数特征:两个自变量和为 时,对应函数值相等。
3.对称性
正弦函数图像关于直线 轴对称
图像上
,两个点的横坐标
关于 为中点坐标时,对应点的纵坐标相等
周期:
最小正周期:
正弦函数
4.周期性
数
形
y
o
x
正弦函数
5.单调性
数
形
y
o
x
在区间
递增
在区间
递减
y
o
x
正弦函数
5.单调性
6.值域(最值)
当
时,
当
时,
值域:
正弦函数
x
正弦函数的零点是
正弦函数
7.零点
形
数
,角的终边落在 轴上
令
x
方法2.观察三角函数图像
用图像认识和发现性质
1.观察图像,理解性质
图像在研究函数性质中的作用?
2.观察图像,发现新性质
正弦函数的图像是轴对称图形,
对称轴:
观察正弦函数 图像,发现新的对称性
观察到的结果是否准确?
需要代数推理证明
证明:
代数特征:两个自变量和为 时函数值相等
正弦函数的图像是轴对称图形,
对称轴:
梳理研究三角函数性质的方法:
三角函数概念,三角函数单位圆模型,
三角函数运算和推理,三角函数图像。
核心:数形结合
与
的图像
观察函数
两个函数图像关于 轴对称
观察到的结果是否准确?
需要代数推理证明
这种研究函数性质的方法有无体验?
用 代替 中的
得到
解析式:
与
的图像关于 轴对称
求证:
图像上任取一点 ,
则点 关于 轴的对称点
证明:在
图像上任一点 关于
轴的对称点 在 上
与
图像关于 轴对称
同理:
梳理研究函数性质的方法:
函数概念
函数解析式或直观模型
数
形
代数运算和推理
梳理研究函数性质的方法:
核心:数形结合
函数概念
函数解析式或直观模型
数
形
代数运算和推理
观察函数图像,猜想性质
形:
“数” 与“形” 的研究方法特点比较
形象、直观
易于发现
缺少准确性
周期
图像法研究性质的局限性:
不准确、无法全部验证…
数:
形:
严谨,有逻辑
形象、直观
证明有难度
易于发现但缺少准确性
以形助数
由数到形
数形结合
“数” 与“形” 的研究方法特点比较
案例1:已知函数
,研究该函数的性质
转化为熟悉的基本初等函数
追问:分析函数解析式、用代数运算研究函数的性质的优势?
已知函数
,研究该函数的性质
函数性质:定义域、对称性、特殊点(零点)、函数值正负区间、周期性、单调性、最值、值域。
已知函数
,研究该函数的性质
对称轴:
非奇非偶函数
周期:
定义域:
值域:
已知函数
,研究该函数的性质
单调递增区间:
零点:
单调递减区间:
英国数学家詹姆斯?西尔维斯特:
“几何看来有时候要领先于分析,但事实上,几何的先行于分析,只不过像一个仆人走在主人的前面一样,是为主人开路的”
函数性质的研究方法
形
数
数形结合
数学的眼光
数学家华罗庚教授:
数缺形时少直观;
形缺数时难入微。
五点作图法
三角函数图像
图像变换法
描点作图
案例2:三角函数性质帮助做三角函数图像
函数性质
函数性质帮助做三角函数图像
三角函数性质——三角函数图像
在 内取几个特殊值
函数性质帮助做三角函数图像
图像关于直线 对称
得到区间 的图像
函数性质帮助做三角函数图像
图像关于原点 对称
得到区间 的图像
函数性质帮助做三角函数图像
周期是
得到整个定义域 上的图像
函数性质帮助做三角函数图像
(1)求 的值,并说明经过哪些运算得到函数值。
问题3.已知函数
四步运算,
四次对应完成
(2)求 在区间 上的最值
分析(1)
是指谁的范围?
(2)
的自变量是谁?
(3)
正弦直接加工的对象是谁?
问题3.已知函数
令
函数值
自变量
函数值
自变量
问题3.已知函数
(2)求 在区间 上的最值
问题3.已知函数
(2)求 在区间 上的最值
解:
令
问题3.已知函数
(2)求 在区间 上的最值
即 时,
当
取得最大值
即 时,
当
取得最小值
变式:若 在 上恒成立,求 的最小值
问题3.已知函数
若 在 上恒成立,
则
(3)求 的单调递增区间
令
函数值
自变量
函数值
自变量
问题3.已知函数
(3)求 的单调递增区间
让
落在 的增区间内
问题3.已知函数
(3)求 的单调递增区间
的单调增区间是
解:因为
的增区间是
变式1:求函数 在 上的单调递增区间
问题3.已知函数
的增区间是
解:因为
又
,所以
当
时,
当
时,
所以 在 上的单调递增区间是
变式2:若函数 在 上单调递增,求 的最大值
问题3.已知函数
的最大值为
问题3.已知函数
变式2:若函数 在 上单调递增,求 的最大值
的单调增区间是
方法二:
由已知得:
的最大值为
(4)把函数 的图像向左平移 个单位,得到函数 是个奇函数,求 的最小值
问题3.已知函数
因为 是 上的奇函数,所以
解:
因为 是 上的奇函数,所以
时
求函数 的最大值和最小值,以及使函数取得最值时的 的值。
问题4.已知函数
分析:观察函数解析式有何特点?
观察角度:角、次数、名称、结构
思路:化余弦为正弦、统一三角函数名称、角
求函数 的最大值和最小值,以及使函数取得最值时的 的值。
解:
令
问题4.已知函数
求函数 的最大值和最小值,以及使函数取得最值时的 的值。
解:
处于
的增区间
处于
的减区间
问题4.已知函数
求函数 的最大值和最小值,以及使函数取得最值时的 的值。
解:
即
或
时,
即
问题4.已知函数
求函数 的最大值和最小值,以及使函数取得最值时的 的值。
即
时,
当
即
时,
当
问题4.已知函数
求函数 的最大值和最小值,以及使函数取得最值时的 的值。
即
时,
当
问题4.已知函数
研究函数性质的方法再认识:
函数概念
函数解析式或直观模型
数
形
代数运算和推理
观察函数图像,猜想性质
研究函数性质的方法再认识:
以形助数
由数到形
数形结合
函数概念
函数解析式或直观模型
数
形
代数运算和推理
观察函数图像,猜想性质
写一篇小论文:
题目:研究函数性质的方法再认识
作业:
感谢收看
祝同学们学习有怀疑、有思考、
有兴趣、有进步!
