华东师大版八年级下册数学19.2.2菱形的判定课件 (共22张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学19.2.2菱形的判定课件 (共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 291.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-21 00:00:00 | ||
图片预览




文档简介
(共22张PPT)
菱形的判定
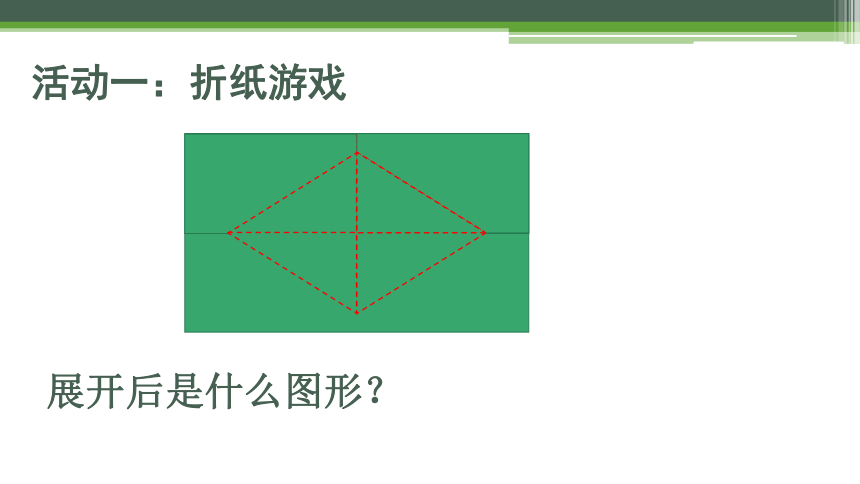
活动一:折纸游戏
展开后是什么图形?
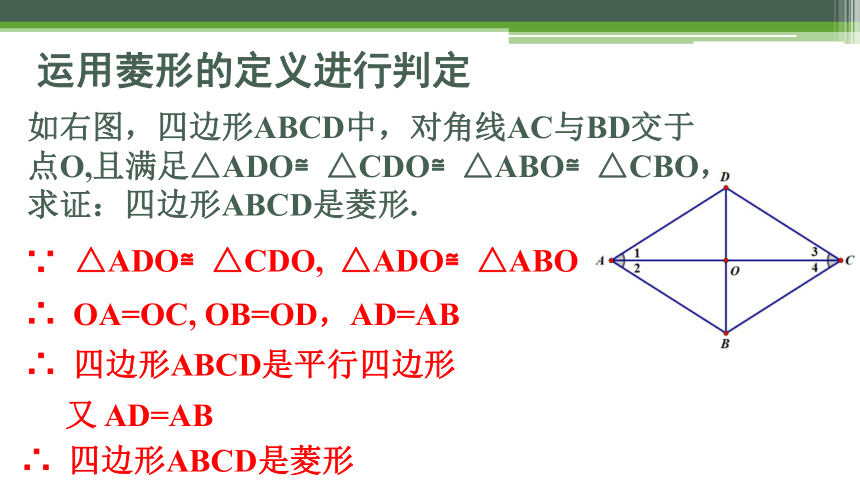
运用菱形的定义进行判定
如右图,四边形ABCD中,对角线AC与BD交于点O,且满足△ADO≌△CDO≌△ABO≌△CBO,
求证:四边形ABCD是菱形.
∵
△ADO≌△CDO,
∴ OA=OC, OB=OD,AD=AB
△ADO≌△ABO
∴ 四边形ABCD是平行四边形
又 AD=AB
∴ 四边形ABCD是菱形
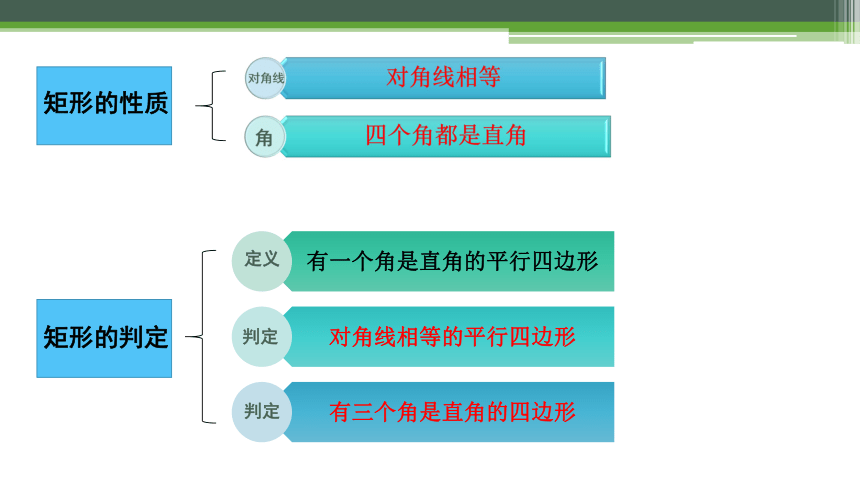
活动二:回忆矩形的性质与判定
边
边
角
对角线
对角线
矩形的性质
定义
矩形的判定
矩形的性质
判定
判定
探究菱形的判定
边
边
角
对角线
对角线
菱形的性质
每条对角线平分一组对角
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形?
猜想:对角线 的 是菱形.
四边形?
平行四边形?
实验操作一
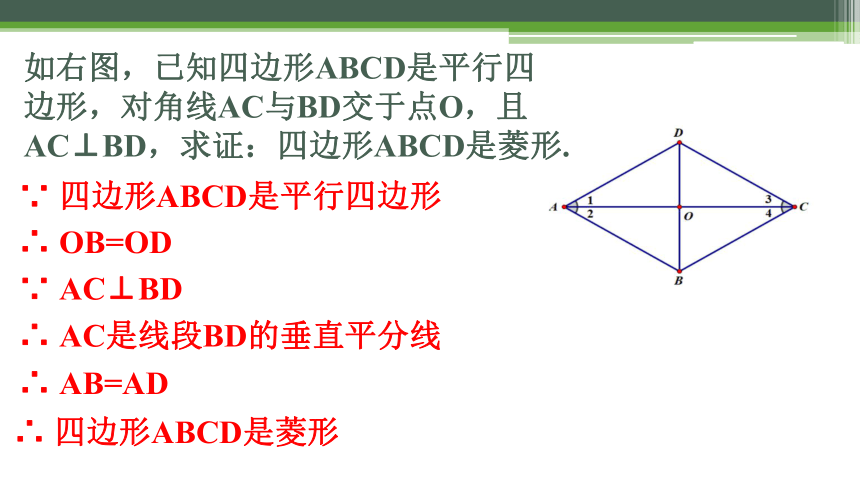
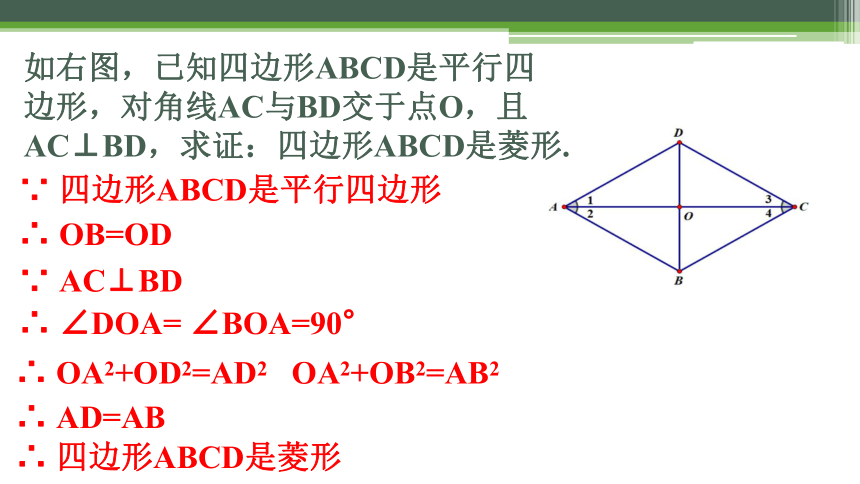
如右图,已知四边形ABCD是平行四边形,对角线AC与BD交于点O,且AC⊥BD,求证:四边形ABCD是菱形.
∵ 四边形ABCD是平行四边形
∴ OB=OD
∵ AC⊥BD
∴ AC是线段BD的垂直平分线
∴ AB=AD
∴ 四边形ABCD是菱形
如右图,已知四边形ABCD是平行四边形,对角线AC与BD交于点O,且AC⊥BD,求证:四边形ABCD是菱形.
∵ 四边形ABCD是平行四边形
∴ OB=OD
∵ AC⊥BD
∴ ∠DOA= ∠BOA=90°
∴ OA2+OD2=AD2 OA2+OB2=AB2
∴ 四边形ABCD是菱形
∴ AD=AB
实验操作二 用直尺和圆规画一个四边相等的四边形
1. 作射线AP,在射线AP上任取一点B;
2. 以A为圆心,AB长为半径画弧,
在弧上任取一点D(异于B点);
3. 分别以B,D为圆心,AB长为半径画弧,
交于点C(异于A点);
猜想:四条边相等的 是菱形.
活动三 知识运用
例:如图,在四边形ABCD中, BD垂直平分线段AC,
且相交于点O,∠1=∠2.
求证:四边形ABCD是菱形.
∵ BD垂直平分线段AC
∴ OA=OC,AC⊥BD ,AB=BC
∵ ∠1= ∠2
∴ ∠AOB= ∠COD= 90°
∴ △AOB≌△COD(AAS)
∴ AB=CD
活动三 知识运用
例:如图,在四边形ABCD中, BD垂直平分线段AC,
且相交于点O,∠1=∠2.
求证:四边形ABCD是菱形.
又∵ ∠1= ∠2
∴ AB∥CD
∴ 四边形ABCD是平行四边形
又AB=BC
∴ 四边形ABCD是菱形
∵ BD垂直平分线段AC
∴ OA=OC,AC⊥BD ,AB=BC
∵ ∠1= ∠2
∴ ∠AOB= ∠COD= 90°
∴ △AOB≌△COD(AAS)
∴ AB=CD
活动三 知识运用
例:如图,在四边形ABCD中, BD垂直平分线段AC,
且相交于点O,∠1=∠2.
求证:四边形ABCD是菱形.
又∵ ∠1= ∠2
∴ AB∥CD
∴ 四边形ABCD是平行四边形
又AB=BC
∴ 四边形ABCD是菱形
又AC⊥BD
∵ BD垂直平分线段AC
∴ OA=OC,AC⊥BD ,AB=BC,AD=DC
∵ ∠1= ∠2
∴ ∠1= ∠OBC, ∠2= ∠ODA,
∴ ∠1= ∠ODA ∠2= ∠OBC
∴ AB=AD BC=BD
活动三 知识运用
例:如图,在四边形ABCD中, BD垂直平分线段AC,
且相交于点O,∠1=∠2.
求证:四边形ABCD是菱形.
∴ AB=AD=BC=BD
∴ 四边形ABCD是菱形
如图四边形ABCD是平行四边形,两条对角线AC、BD相交于点O,AB=5,AC=8,DB=6
求证:四边形ABCD是菱形.
如图矩形ABCD中,E,F,G,H分别是AD,AB,BC,CD的中点.
求证:四边形EHGF是菱形.
性质:菱形的每一条对角线平分一组对角
一条对角线平分一组对角的 是菱形.
两条对角线分别平分一组对角的 是菱形.
四边形?
平行四边形?
一条对角线平分一组对角的 是菱形.
已知 中,∠1=∠2,∠3=∠4,求证:四边形
ABCD是菱形.
两条对角线分别平分一组对角的 是菱形.
已知 中,∠1=∠2,∠3=∠4,∠ADO=∠CDO,
∠ABO=∠CBO 求证:四边形ABCD是菱形.
如右图,四边形ABCD中,对角线AC与BD交于点O,且满足△ADO≌△CDO≌△ABO≌△CBO,
求证:四边形ABCD是菱形.
∵
△ADO≌△CDO,
∴ OA=OC, OB=OD,AD=AB
△ADO≌△ABO
∴ 四边形ABCD是平行四边形
又 AD=AB
∴ 四边形ABCD是菱形
课堂总结
一组邻边相等的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
四条边相等的四边形是菱形.
优胜小组评选
青春飞扬
青春旋律
青春年华
青春活力
青春氤氲
青春星阑
我们的口号是!
飞扬拼搏 激情活力
旋律氤氲 争创佳绩
年华无限 星阑传奇
青春八二 天下无敌
菱形的判定
活动一:折纸游戏
展开后是什么图形?
运用菱形的定义进行判定
如右图,四边形ABCD中,对角线AC与BD交于点O,且满足△ADO≌△CDO≌△ABO≌△CBO,
求证:四边形ABCD是菱形.
∵
△ADO≌△CDO,
∴ OA=OC, OB=OD,AD=AB
△ADO≌△ABO
∴ 四边形ABCD是平行四边形
又 AD=AB
∴ 四边形ABCD是菱形
活动二:回忆矩形的性质与判定
边
边
角
对角线
对角线
矩形的性质
定义
矩形的判定
矩形的性质
判定
判定
探究菱形的判定
边
边
角
对角线
对角线
菱形的性质
每条对角线平分一组对角
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形?
猜想:对角线 的 是菱形.
四边形?
平行四边形?
实验操作一
如右图,已知四边形ABCD是平行四边形,对角线AC与BD交于点O,且AC⊥BD,求证:四边形ABCD是菱形.
∵ 四边形ABCD是平行四边形
∴ OB=OD
∵ AC⊥BD
∴ AC是线段BD的垂直平分线
∴ AB=AD
∴ 四边形ABCD是菱形
如右图,已知四边形ABCD是平行四边形,对角线AC与BD交于点O,且AC⊥BD,求证:四边形ABCD是菱形.
∵ 四边形ABCD是平行四边形
∴ OB=OD
∵ AC⊥BD
∴ ∠DOA= ∠BOA=90°
∴ OA2+OD2=AD2 OA2+OB2=AB2
∴ 四边形ABCD是菱形
∴ AD=AB
实验操作二 用直尺和圆规画一个四边相等的四边形
1. 作射线AP,在射线AP上任取一点B;
2. 以A为圆心,AB长为半径画弧,
在弧上任取一点D(异于B点);
3. 分别以B,D为圆心,AB长为半径画弧,
交于点C(异于A点);
猜想:四条边相等的 是菱形.
活动三 知识运用
例:如图,在四边形ABCD中, BD垂直平分线段AC,
且相交于点O,∠1=∠2.
求证:四边形ABCD是菱形.
∵ BD垂直平分线段AC
∴ OA=OC,AC⊥BD ,AB=BC
∵ ∠1= ∠2
∴ ∠AOB= ∠COD= 90°
∴ △AOB≌△COD(AAS)
∴ AB=CD
活动三 知识运用
例:如图,在四边形ABCD中, BD垂直平分线段AC,
且相交于点O,∠1=∠2.
求证:四边形ABCD是菱形.
又∵ ∠1= ∠2
∴ AB∥CD
∴ 四边形ABCD是平行四边形
又AB=BC
∴ 四边形ABCD是菱形
∵ BD垂直平分线段AC
∴ OA=OC,AC⊥BD ,AB=BC
∵ ∠1= ∠2
∴ ∠AOB= ∠COD= 90°
∴ △AOB≌△COD(AAS)
∴ AB=CD
活动三 知识运用
例:如图,在四边形ABCD中, BD垂直平分线段AC,
且相交于点O,∠1=∠2.
求证:四边形ABCD是菱形.
又∵ ∠1= ∠2
∴ AB∥CD
∴ 四边形ABCD是平行四边形
又AB=BC
∴ 四边形ABCD是菱形
又AC⊥BD
∵ BD垂直平分线段AC
∴ OA=OC,AC⊥BD ,AB=BC,AD=DC
∵ ∠1= ∠2
∴ ∠1= ∠OBC, ∠2= ∠ODA,
∴ ∠1= ∠ODA ∠2= ∠OBC
∴ AB=AD BC=BD
活动三 知识运用
例:如图,在四边形ABCD中, BD垂直平分线段AC,
且相交于点O,∠1=∠2.
求证:四边形ABCD是菱形.
∴ AB=AD=BC=BD
∴ 四边形ABCD是菱形
如图四边形ABCD是平行四边形,两条对角线AC、BD相交于点O,AB=5,AC=8,DB=6
求证:四边形ABCD是菱形.
如图矩形ABCD中,E,F,G,H分别是AD,AB,BC,CD的中点.
求证:四边形EHGF是菱形.
性质:菱形的每一条对角线平分一组对角
一条对角线平分一组对角的 是菱形.
两条对角线分别平分一组对角的 是菱形.
四边形?
平行四边形?
一条对角线平分一组对角的 是菱形.
已知 中,∠1=∠2,∠3=∠4,求证:四边形
ABCD是菱形.
两条对角线分别平分一组对角的 是菱形.
已知 中,∠1=∠2,∠3=∠4,∠ADO=∠CDO,
∠ABO=∠CBO 求证:四边形ABCD是菱形.
如右图,四边形ABCD中,对角线AC与BD交于点O,且满足△ADO≌△CDO≌△ABO≌△CBO,
求证:四边形ABCD是菱形.
∵
△ADO≌△CDO,
∴ OA=OC, OB=OD,AD=AB
△ADO≌△ABO
∴ 四边形ABCD是平行四边形
又 AD=AB
∴ 四边形ABCD是菱形
课堂总结
一组邻边相等的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
四条边相等的四边形是菱形.
优胜小组评选
青春飞扬
青春旋律
青春年华
青春活力
青春氤氲
青春星阑
我们的口号是!
飞扬拼搏 激情活力
旋律氤氲 争创佳绩
年华无限 星阑传奇
青春八二 天下无敌
