人教版七年级下册数学第六章实数 复习小结 课件 (共29张PPT)
文档属性
| 名称 | 人教版七年级下册数学第六章实数 复习小结 课件 (共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-21 11:15:49 | ||
图片预览







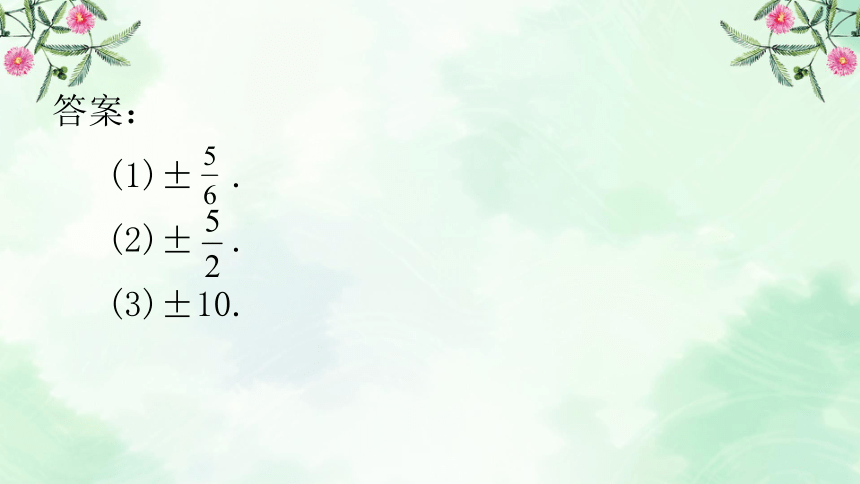
文档简介
(共29张PPT)
实数 复习小结
第六章
01
03
02
04
目录
学习目标
学习重难点
本章知识体系
专题复习
1、学习目标
(1)开方 乘方,会求算数平方根、平方根、立方根。
(2)掌握无理数和实数的概念,实数 数轴上的点。
(3)会用根号表示数的平方根、立方根,会求某些非负数的平方根,用求某些数的立方根,能用计算器计算平方根、立方根。估算无理数的范围。
(4)能进行简单的实数四则运算.
逆运算
一一对应
算数平方根、平方根、立方根、无理数、实数的概念及其相关运算.
难点
重点
1.平方根和立方根的概念.
2.实数的简单四则运算.
2、学习重难点
3、本章知识体系
算数平方根
平方根
数的开方
立方根
用计算器求平方根、立方根
无理数
分类
有理数
相反数
实 数 有关概念
绝对值
与数轴上的点一一对应 比较大小
近似计算
4、专题复习
专题一 平方根、立方根的概念
专题二 实数的有关概念及计算
专题三 数形结合思想
专题四 非负数的性质及应用
专题一 平方根、立方根的概念
01 点击输入标题内容
平方根、立方根的概念是把有理数学习拓展到实数学习的开始,平方根和立方根的知识在实数中占有非常重要的地位..
解答此类问题主要注意以下几点:
1、是开平方和开立方的区别;
2、是熟悉计算器的使用;
3、是看题目的要求,弄清被开方数.
例1 求下列各数的平方根.
(1) ; (2)6 ; (3)(-10)?.
答案:
(1)± .
(2)± .
(3)±10.
【针对训练1】
(1)求下列各式的值.
① ;②- ; ③± .
(2)①- ②-
③ ④
3
(1)① 20
②-
③±
答案:
(2)①- ② ③ - ④-6
例2 要到玻璃店配一块面积为1.21 m?的正方形玻璃,那么该玻璃的边长为 m.
1.1
正方形的边长是其面积的算术平方根,
用开平方或开立方解决实际问题,要注意计算结果的实际意义.
【针对训练2】
已知b=a3+2c,其中b的算术平方根为19,c的平方根是±3,求a的值.
解:因为b的算术平方根是19,
所以b=192=361.
因为c的平方根是±3,所以c=(±3)2=9.
所以a3=b-2c=361-18=343, a=7.
例3 用计算器求21.52的平方根(精确
到0.001).
答 案:约等于 ±4.639.
【针对训练3】 用计算器计算 的值.(精确到0.001)
解: ≈1.871.
注意:输入被开方数时应输入
334÷(17×3).
专题二 实数的有关概念及计算
例4 在-7.5 , , 4 , ,-π ,0.15 , 中,无理数的个数是 ( )
A.1 B.2 C.3 D.4
··
B
【针对训练4】 下列实数 , , ,( ) 0 , 3.14159,- ,(- )2 , 中无理数的个数是 ( )
A.1 B.2 C.3 D.4
3
2
π
〔解析〕 对实数进行分类不能只看表面形式,应先化简,再根据结果去判断
C
= .
例5 计算(- )- (- )+ (- )
-
有理数的四则运算法则适用于无理数的计算
【针对训练5】
已知 ≈0.8138, ≈3.777,
≈1.753,则 ≈
≈
〔解析〕 开立方运算时要注意小数点的变化规律,开立方是三位与一位的关系,开平方是二位与一位的关系.
0.08138
37.77
例6 比较3 -1与1+2 的大小.
〔解析〕运用比差法,当a-b=0时,可知a=b;
当a-b>0时,可知a>b,
当a-b<0时,可知a解:因为(3 -1)-(1+2 )
=3 -1-1-2
=-2+
所以3 -1<1+2 .
<0
【针对训练6】 比较 2 和3 的大小.
〔解析〕 当a>0,b>0时,a>b?a2>b2.
解:因为(2 )2=12, (3 )2=18, 12<18,
所以2 <3 .
专题三 数形结合思想
把实数在数轴上直观地表示出来,可以形象、直观地感受实数的客观存在,实数和数轴上的点一一对应.
借助于数轴比较实数大小、实数化简、直角坐标系内的相关计算等.
例7 实数a,b在数轴上的位置如图所示,化简|a+b|+ (b-a)2 .
〔解析〕去绝对值和根号,此时只要分别判断a+b和b-a的符号即可.
a
0
b
解:由图可知a<0,b>0,且|a|>|b|.
所以a+b<0 , b-a>0,
所以|a+b|+ (b-a)2=-(a+b)+(b-a)=-2a.
【针对训练7】 如图所示,在数轴上点A和B之间的整数点有 个.?
`
〔解析〕 解本题的关键是确定-与之间有哪些整数,由于-2<- <-1,2< <3,所以- 与之 间的整数有-1,0,1,2,所以A,B两点之间的整数点有4个.故填4.
-
A
B
0
4
例8已知数轴上有A,B两点,且这两点之间的距离为4 ,若点A在数轴上表示的数为3 ,则点B在数轴上表示的数为 .?
〔解析〕本题运用绝对值的知识来解,若数轴上A点表示的数为a,B点表示的数为b,则A、B两点之间的距离为|a-b|,设B点在数轴上表示的数为b,则|3 -b|=4 ,解得b=7 或- .
7 或-
【针对训练8】 实数a,b在数轴上的位置如图所示,化简|a-b|- a2 的结果是 ( )
A.2a-b B.b C.-b D.-2a+b
b
0
a
〔解析〕由数轴知a>0,b<0,|a|>|b|,所以a-b>0,所以|a-b|- a2=a-b-a=-b.故选C.
C
专题四 非负数的性质及应用
例9 若 2x-1 与│1+y│互为相反数,则
x2+y2= .
√
〔解析〕2x-1=0,1+y=0 .
所以 x= y=-1
【针对训练9】若 √x-1 +(y+2)2=0,则(x+y)2014等于 ( )
A.-1 B.1 C.32014 D.-32014
〔解析〕x-1 =0,y+2=0
所以x=1,y=-2,x+y=-1
(x+y)2014=(-1)2014=1
B
祝大家学习进步!
实数 复习小结
第六章
01
03
02
04
目录
学习目标
学习重难点
本章知识体系
专题复习
1、学习目标
(1)开方 乘方,会求算数平方根、平方根、立方根。
(2)掌握无理数和实数的概念,实数 数轴上的点。
(3)会用根号表示数的平方根、立方根,会求某些非负数的平方根,用求某些数的立方根,能用计算器计算平方根、立方根。估算无理数的范围。
(4)能进行简单的实数四则运算.
逆运算
一一对应
算数平方根、平方根、立方根、无理数、实数的概念及其相关运算.
难点
重点
1.平方根和立方根的概念.
2.实数的简单四则运算.
2、学习重难点
3、本章知识体系
算数平方根
平方根
数的开方
立方根
用计算器求平方根、立方根
无理数
分类
有理数
相反数
实 数 有关概念
绝对值
与数轴上的点一一对应 比较大小
近似计算
4、专题复习
专题一 平方根、立方根的概念
专题二 实数的有关概念及计算
专题三 数形结合思想
专题四 非负数的性质及应用
专题一 平方根、立方根的概念
01 点击输入标题内容
平方根、立方根的概念是把有理数学习拓展到实数学习的开始,平方根和立方根的知识在实数中占有非常重要的地位..
解答此类问题主要注意以下几点:
1、是开平方和开立方的区别;
2、是熟悉计算器的使用;
3、是看题目的要求,弄清被开方数.
例1 求下列各数的平方根.
(1) ; (2)6 ; (3)(-10)?.
答案:
(1)± .
(2)± .
(3)±10.
【针对训练1】
(1)求下列各式的值.
① ;②- ; ③± .
(2)①- ②-
③ ④
3
(1)① 20
②-
③±
答案:
(2)①- ② ③ - ④-6
例2 要到玻璃店配一块面积为1.21 m?的正方形玻璃,那么该玻璃的边长为 m.
1.1
正方形的边长是其面积的算术平方根,
用开平方或开立方解决实际问题,要注意计算结果的实际意义.
【针对训练2】
已知b=a3+2c,其中b的算术平方根为19,c的平方根是±3,求a的值.
解:因为b的算术平方根是19,
所以b=192=361.
因为c的平方根是±3,所以c=(±3)2=9.
所以a3=b-2c=361-18=343, a=7.
例3 用计算器求21.52的平方根(精确
到0.001).
答 案:约等于 ±4.639.
【针对训练3】 用计算器计算 的值.(精确到0.001)
解: ≈1.871.
注意:输入被开方数时应输入
334÷(17×3).
专题二 实数的有关概念及计算
例4 在-7.5 , , 4 , ,-π ,0.15 , 中,无理数的个数是 ( )
A.1 B.2 C.3 D.4
··
B
【针对训练4】 下列实数 , , ,( ) 0 , 3.14159,- ,(- )2 , 中无理数的个数是 ( )
A.1 B.2 C.3 D.4
3
2
π
〔解析〕 对实数进行分类不能只看表面形式,应先化简,再根据结果去判断
C
= .
例5 计算(- )- (- )+ (- )
-
有理数的四则运算法则适用于无理数的计算
【针对训练5】
已知 ≈0.8138, ≈3.777,
≈1.753,则 ≈
≈
〔解析〕 开立方运算时要注意小数点的变化规律,开立方是三位与一位的关系,开平方是二位与一位的关系.
0.08138
37.77
例6 比较3 -1与1+2 的大小.
〔解析〕运用比差法,当a-b=0时,可知a=b;
当a-b>0时,可知a>b,
当a-b<0时,可知a
=3 -1-1-2
=-2+
所以3 -1<1+2 .
<0
【针对训练6】 比较 2 和3 的大小.
〔解析〕 当a>0,b>0时,a>b?a2>b2.
解:因为(2 )2=12, (3 )2=18, 12<18,
所以2 <3 .
专题三 数形结合思想
把实数在数轴上直观地表示出来,可以形象、直观地感受实数的客观存在,实数和数轴上的点一一对应.
借助于数轴比较实数大小、实数化简、直角坐标系内的相关计算等.
例7 实数a,b在数轴上的位置如图所示,化简|a+b|+ (b-a)2 .
〔解析〕去绝对值和根号,此时只要分别判断a+b和b-a的符号即可.
a
0
b
解:由图可知a<0,b>0,且|a|>|b|.
所以a+b<0 , b-a>0,
所以|a+b|+ (b-a)2=-(a+b)+(b-a)=-2a.
【针对训练7】 如图所示,在数轴上点A和B之间的整数点有 个.?
`
〔解析〕 解本题的关键是确定-与之间有哪些整数,由于-2<- <-1,2< <3,所以- 与之 间的整数有-1,0,1,2,所以A,B两点之间的整数点有4个.故填4.
-
A
B
0
4
例8已知数轴上有A,B两点,且这两点之间的距离为4 ,若点A在数轴上表示的数为3 ,则点B在数轴上表示的数为 .?
〔解析〕本题运用绝对值的知识来解,若数轴上A点表示的数为a,B点表示的数为b,则A、B两点之间的距离为|a-b|,设B点在数轴上表示的数为b,则|3 -b|=4 ,解得b=7 或- .
7 或-
【针对训练8】 实数a,b在数轴上的位置如图所示,化简|a-b|- a2 的结果是 ( )
A.2a-b B.b C.-b D.-2a+b
b
0
a
〔解析〕由数轴知a>0,b<0,|a|>|b|,所以a-b>0,所以|a-b|- a2=a-b-a=-b.故选C.
C
专题四 非负数的性质及应用
例9 若 2x-1 与│1+y│互为相反数,则
x2+y2= .
√
〔解析〕2x-1=0,1+y=0 .
所以 x= y=-1
【针对训练9】若 √x-1 +(y+2)2=0,则(x+y)2014等于 ( )
A.-1 B.1 C.32014 D.-32014
〔解析〕x-1 =0,y+2=0
所以x=1,y=-2,x+y=-1
(x+y)2014=(-1)2014=1
B
祝大家学习进步!
