辽宁省鞍山市五校联盟八年级数学下册(三角形中位线复习题)学案(无答案)
文档属性
| 名称 | 辽宁省鞍山市五校联盟八年级数学下册(三角形中位线复习题)学案(无答案) |
|
|
| 格式 | rar | ||
| 文件大小 | 191.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-22 00:00:00 | ||
图片预览

文档简介
三角形中位线复习题
【知识梳理】
考点十、三角形的中位线问题
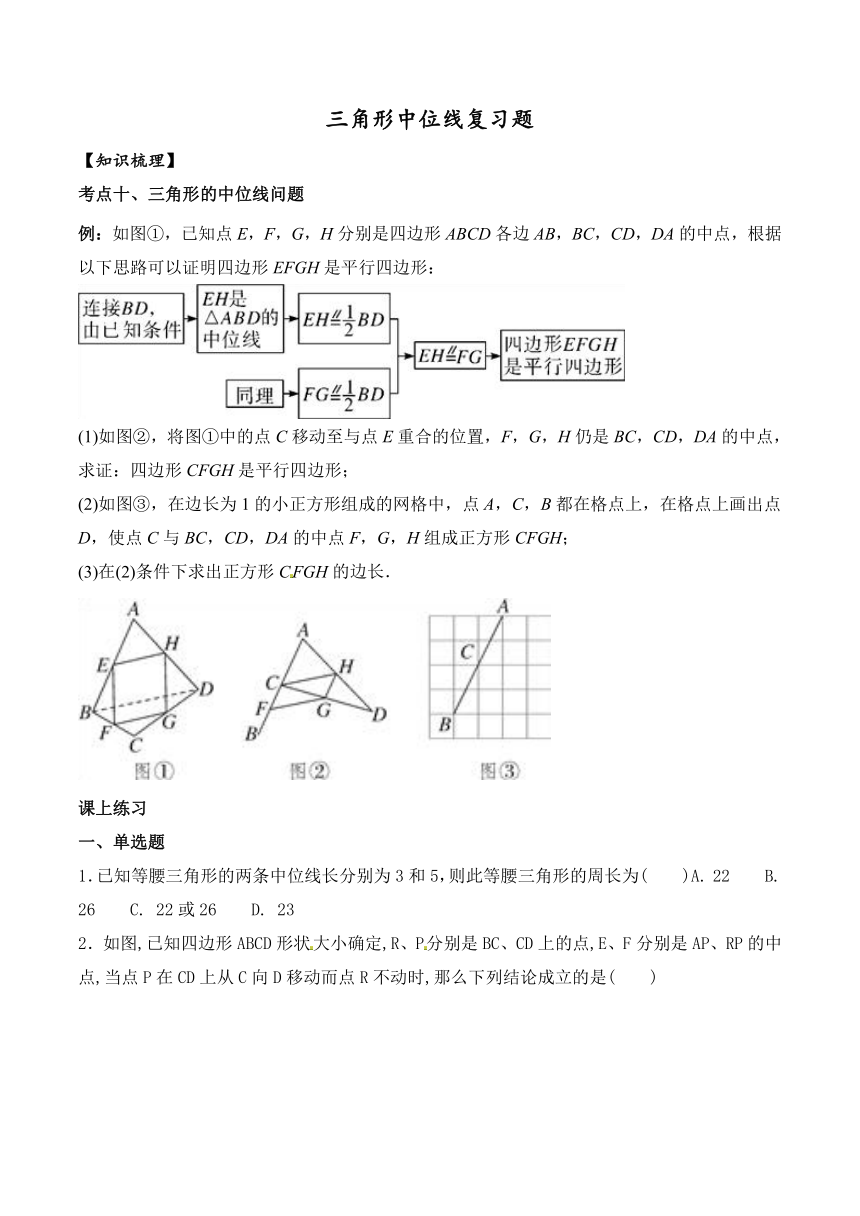
例:如图①,已知点E,F,G,H分别是四边形ABCD各边AB,BC,CD,DA的中点,根据以下思路可以证明四边形EFGH是平行四边形:
[来*]
(1)如图②,将图①中的点C移动至与点E重合的位置,F,G,H仍是BC,CD,DA的中点,求证:四边形CFGH是平行四边形;
(2)如图③,在边长为1的小正方形组成的网格中,点A,C,B都在格点上,在格点上画出点D,使点C与BC,CD,DA的中点F,G,H组成正方形CFGH;
(3)在(2)条件下求出正方形CFGH的边长.
课上练习
一、单选题
1.已知等腰三角形的两条中位线长分别为3和5,则此等腰三角形的周长为( )A. 22 B. 26 C. 22或26 D. 23
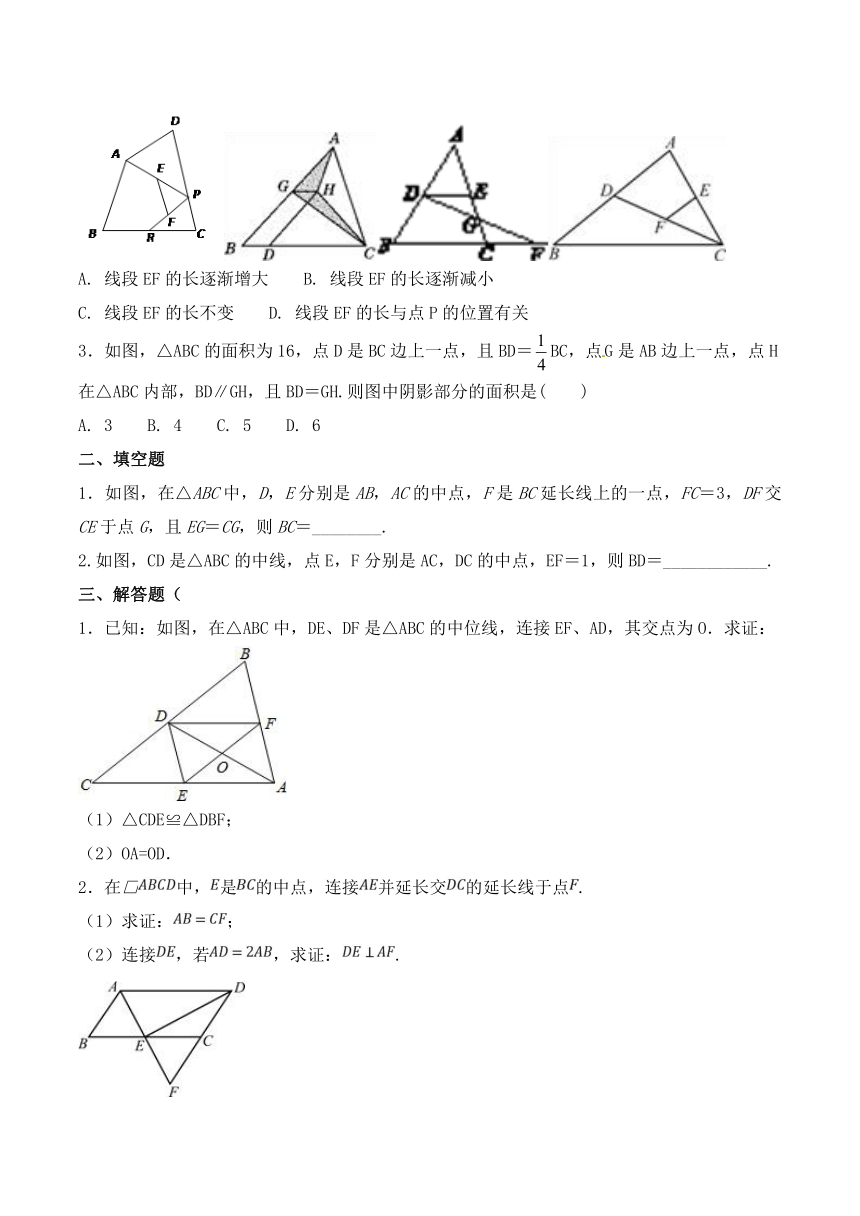
2.如图,已知四边形ABCD形状大小确定,R、P分别是BC、CD上的点,E、F分别是AP、RP的中点,当点P在CD上从C向D移动而点R不动时,那么下列结论成立的是( )
A. 线段EF的长逐渐增大 B. 线段EF的长逐渐减小
C. 线段EF的长不变 D. 线段EF的长与点P的位置有关
3.如图,△ABC的面积为16,点D是BC边上一点,且BD=BC,点G是AB边上一点,点H在△ABC内部,BD∥GH,且BD=GH.则图中阴影部分的面积是( )
A. 3 B. 4 C. 5 D. 6
二、填空题
1.如图,在△ABC中,D,E分别是AB,AC的中点,F是BC延长线上的一点,FC=3,DF交CE于点G,且EG=CG,则BC=________.
2.如图,CD是△ABC的中线,点E,F分别是AC,DC的中点,EF=1,则BD=____________.
三、解答题(
1.已知:如图,在△ABC中,DE、DF是△ABC的中位线,连接EF、AD,其交点为O.求证:
(1)△CDE≌△DBF;
(2)OA=OD.
2.在□中,是的中点,连接并延长交的延长线于点.
(1)求证:;
(2)连接,若,求证:.
课后作业
一、填空题:
1. (1)三角形的中位线的定义:连结三角形两边____________叫做三角形的中位线.
(2)三角形的中位线定理是三角形的中位线________第三边,并且等于___________.
2. 如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,A′、B′、C′分别为EF、EG、GF的中点,△A′B′C′的周长为_________.如果△ABC、△EFG、△A′B′C′分别为第1个、第2个、第3个三角形,按照上述方法继续作三角形,那么第n个三角形的周长是__________________.
3. △ABC中,D、E分别为AB、AC的中点,若DE=4,AD=3,AE=2,则△ABC的周长为______.
二、解答题
4. 已知:如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形.
5. 已知:△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点.求证:四边形DEFG是平行四边形.
6. 已知:如图,E为□ABCD中DC边的延长线上的一点,且CE=DC,连结AE分别交BC、BD于点F、G,连结AC交BD于O,连结OF.求证:AB=2OF.
7. 已知:如图,在□ABCD中,E是CD的中点,F是AE的中点,FC与BE交于G.求证:GF=GC.
8. 已知:如图,在四边形ABCD中,AD=BC,E、F分别是DC、AB边的中点,FE的延长线分别与AD、BC的延长线交于H、G点.求证:∠AHF=∠BGF.
9. 已知:如图,△ABC中,D是BC边的中点,AE平分∠BAC,BE⊥AE于E点,若AB=5,AC=7,求ED.
10. 如图在△ABC中,D、E分别为AB、AC上的点,且BD=CE,M、N分别是BE、CD的中点.过MN的直线交AB于P,交AC于Q,线段AP、AQ相等吗?为什么?
【知识梳理】
考点十、三角形的中位线问题
例:如图①,已知点E,F,G,H分别是四边形ABCD各边AB,BC,CD,DA的中点,根据以下思路可以证明四边形EFGH是平行四边形:
[来*]
(1)如图②,将图①中的点C移动至与点E重合的位置,F,G,H仍是BC,CD,DA的中点,求证:四边形CFGH是平行四边形;
(2)如图③,在边长为1的小正方形组成的网格中,点A,C,B都在格点上,在格点上画出点D,使点C与BC,CD,DA的中点F,G,H组成正方形CFGH;
(3)在(2)条件下求出正方形CFGH的边长.
课上练习
一、单选题
1.已知等腰三角形的两条中位线长分别为3和5,则此等腰三角形的周长为( )A. 22 B. 26 C. 22或26 D. 23
2.如图,已知四边形ABCD形状大小确定,R、P分别是BC、CD上的点,E、F分别是AP、RP的中点,当点P在CD上从C向D移动而点R不动时,那么下列结论成立的是( )
A. 线段EF的长逐渐增大 B. 线段EF的长逐渐减小
C. 线段EF的长不变 D. 线段EF的长与点P的位置有关
3.如图,△ABC的面积为16,点D是BC边上一点,且BD=BC,点G是AB边上一点,点H在△ABC内部,BD∥GH,且BD=GH.则图中阴影部分的面积是( )
A. 3 B. 4 C. 5 D. 6
二、填空题
1.如图,在△ABC中,D,E分别是AB,AC的中点,F是BC延长线上的一点,FC=3,DF交CE于点G,且EG=CG,则BC=________.
2.如图,CD是△ABC的中线,点E,F分别是AC,DC的中点,EF=1,则BD=____________.
三、解答题(
1.已知:如图,在△ABC中,DE、DF是△ABC的中位线,连接EF、AD,其交点为O.求证:
(1)△CDE≌△DBF;
(2)OA=OD.
2.在□中,是的中点,连接并延长交的延长线于点.
(1)求证:;
(2)连接,若,求证:.
课后作业
一、填空题:
1. (1)三角形的中位线的定义:连结三角形两边____________叫做三角形的中位线.
(2)三角形的中位线定理是三角形的中位线________第三边,并且等于___________.
2. 如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,A′、B′、C′分别为EF、EG、GF的中点,△A′B′C′的周长为_________.如果△ABC、△EFG、△A′B′C′分别为第1个、第2个、第3个三角形,按照上述方法继续作三角形,那么第n个三角形的周长是__________________.
3. △ABC中,D、E分别为AB、AC的中点,若DE=4,AD=3,AE=2,则△ABC的周长为______.
二、解答题
4. 已知:如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形.
5. 已知:△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点.求证:四边形DEFG是平行四边形.
6. 已知:如图,E为□ABCD中DC边的延长线上的一点,且CE=DC,连结AE分别交BC、BD于点F、G,连结AC交BD于O,连结OF.求证:AB=2OF.
7. 已知:如图,在□ABCD中,E是CD的中点,F是AE的中点,FC与BE交于G.求证:GF=GC.
8. 已知:如图,在四边形ABCD中,AD=BC,E、F分别是DC、AB边的中点,FE的延长线分别与AD、BC的延长线交于H、G点.求证:∠AHF=∠BGF.
9. 已知:如图,△ABC中,D是BC边的中点,AE平分∠BAC,BE⊥AE于E点,若AB=5,AC=7,求ED.
10. 如图在△ABC中,D、E分别为AB、AC上的点,且BD=CE,M、N分别是BE、CD的中点.过MN的直线交AB于P,交AC于Q,线段AP、AQ相等吗?为什么?
