高中物理人教版必修2 5.4圆周运动 导学案
文档属性
| 名称 | 高中物理人教版必修2 5.4圆周运动 导学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 688.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-05-21 00:00:00 | ||
图片预览

文档简介
第五章第3讲:圆周运动(1)
学习目标:
.从运动学角度理解描述圆周运动的物理量,理解各物理量间的关系
从动力学角度分析向心力的来源。
重难点:
传动装置
分析向心力来源的思路
导学流程:
1.匀速圆周运动
(1)定义:做圆周运动的物体,若在任意相等的时间内通过的圆弧长相等,就是匀速圆周运动.
(2)特点:加速度大小不变,方向始终指向圆心,是变加速运动.
(3)条件:合外力大小不变、方向始终与速度方向垂直且指向圆心.
2.运动参量
定义、意义 公式、单位
线速度 描述做圆周运动的物体沿圆弧运动快慢的物理量(v) (1)v== (2)单位:m/s
角速度 描述物体绕圆心转动快慢的物理量(ω) (1)ω== (2)单位:rad/s
周期 物体沿圆周运动一圈的时间(T) (1)T==,单位:s (2)f=,单位:Hz
向心加速度 (1)描述速度方向变化快慢的物理量(an) (2)方向指向圆心 (1)an==rω2 (2)单位:m/s2
二、匀速圆周运动的向心力
1.作用效果
向心力产生向心加速度,只改变速度的方向,不改变速度的大小.
2.大小
F=m=mrω2=mr=mωv=4π2mf2r.
3.方向
始终沿半径方向指向圆心,时刻在改变,即向心力是一个变力.
4.来源
向心力可以由一个力提供,也可以由几个力的合力提供,还可以由一个力的分力提供
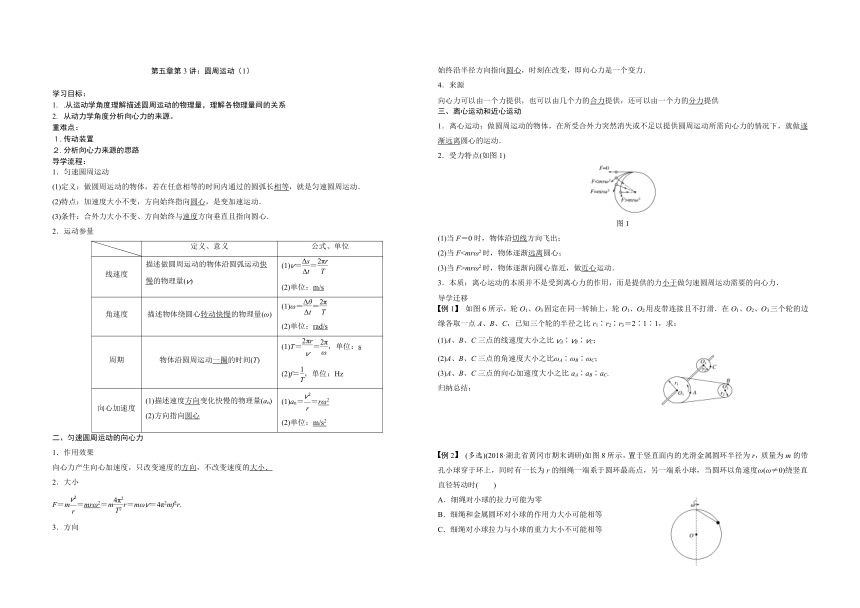
三、离心运动和近心运动
1.离心运动:做圆周运动的物体,在所受合外力突然消失或不足以提供圆周运动所需向心力的情况下,就做逐渐远离圆心的运动.
2.受力特点(如图1)
图1
(1)当F=0时,物体沿切线方向飞出;
(2)当F
3.本质:离心运动的本质并不是受到离心力的作用,而是提供的力小于做匀速圆周运动需要的向心力.
导学迁移
例1 如图6所示,轮O1、O3固定在同一转轴上,轮O1、O2用皮带连接且不打滑.在O1、O2、O3三个轮的边缘各取一点A、B、C,已知三个轮的半径之比r1∶r2∶r3=2∶1∶1,求:
(1)A、B、C三点的线速度大小之比vA∶vB∶vC;
(2)A、B、C三点的角速度大小之比ωA∶ωB∶ωC;
(3)A、B、C三点的向心加速度大小之比aA∶aB∶aC.
归纳总结:
例2 (多选)(2018·湖北省黄冈市期末调研)如图8所示,置于竖直面内的光滑金属圆环半径为r,质量为m的带孔小球穿于环上,同时有一长为r的细绳一端系于圆环最高点,另一端系小球,当圆环以角速度ω(ω≠0)绕竖直直径转动时( )
A.细绳对小球的拉力可能为零
B.细绳和金属圆环对小球的作用力大小可能相等
C.细绳对小球拉力与小球的重力大小不可能相等
D.当ω=时,金属圆环对小球的作用力为零
.归纳总结;1分析向心力来源的思路
2.运动模型
运动模型 向心力的来源图示
飞机水平转弯
火车转弯
圆锥摆
飞车走壁
汽车在水平路面转弯
水平转台(光滑)
例3(多选)如图所示,一同学做飞镖游戏,悬挂在竖直墙面上半径的圆盘绕垂直圆盘过圆心的水平轴匀速转动。当点转动到圆周的最高点时,一飞镖(看作质点)对着点正上方以初速度水平抛出。飞镖抛出点距圆盘的水平距离为,与圆盘上边缘高度差。若飞镖击中圆盘直径上的点则该同学取得游戏的胜利,要取得游戏的胜利(取),下列关系式正确的是( )
A.初速度为或
B.圆盘匀速转动的角速度为(、2、3…)
C.飞镖击中圆盘的速度方向或(为速度与竖直方向的夹角)
D.飞镖击中点时的速率
变式1 (多选)(2019·辽宁省丹东市质检)在如图7所示的齿轮传动中,三个齿轮的半径之比为2∶3∶6,当齿轮转动的时候,关于小齿轮边缘的A点和大齿轮边缘的B点,( )
A.A点和B点的线速度大小之比为1∶1
B.A点和B点的角速度之比为1∶1
C.A点和B点的角速度之比为3∶1
D.以上三个选项只有一个是正确的
变式2 (多选)(2018·甘肃省兰州一中模拟)在修筑铁路时,弯道处的外轨会略高于内轨.如图9所示,当火车以规定的行驶速度转弯时,内、外轨均不会受到轮缘的挤压,设此时的速度大小为v,重力加速度为g,两轨所在面的倾角为θ,则( )
A.该弯道的半径r=
B.当火车质量改变时,规定的行驶速度大小不变
C.当火车速率大于v时,内轨将受到轮缘的挤压
D.当火车速率大于v时,外轨将受到轮缘的挤压
