六年级下册数学课件 第1单元 圆柱与圆锥整理与复习 (共20张PPT)北师大版
文档属性
| 名称 | 六年级下册数学课件 第1单元 圆柱与圆锥整理与复习 (共20张PPT)北师大版 |  | |
| 格式 | zip | ||
| 文件大小 | 768.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-21 16:25:45 | ||
图片预览






文档简介
(共20张PPT)
整理与复习
考点1
面的旋转
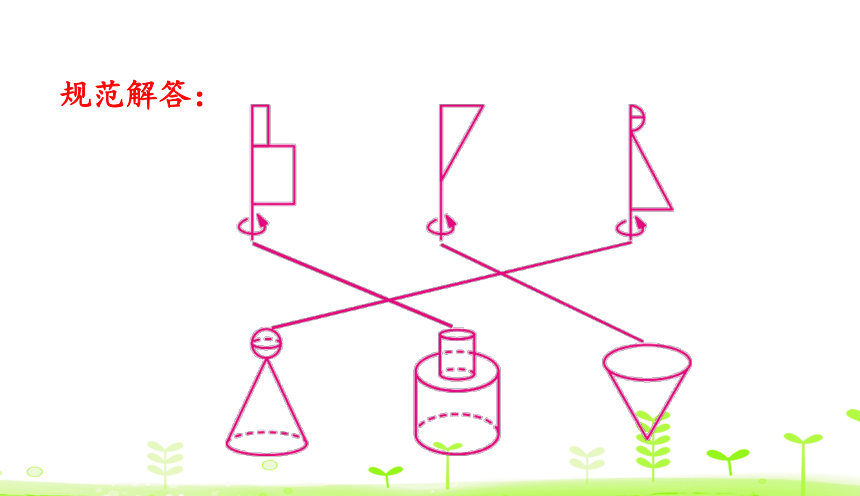
例 1 下面的图形旋转一周,可以得到哪个立体图形?
用线连一连。
思路分析:1. 想象长方形、直角三角形、半圆旋
转后形成的图形。
2. 分别把旋转后形成的图形组合起来,
再连线。
规范解答:
考点 2
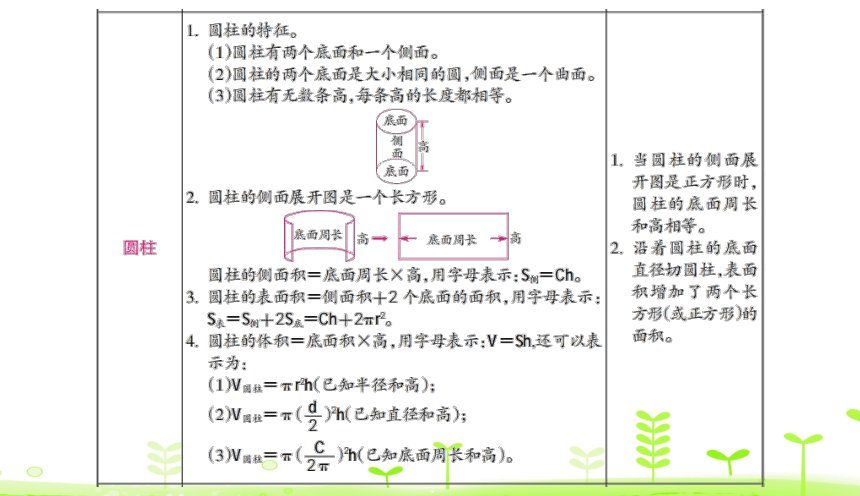
圆柱的表面积
例 2 做一个无盖的圆柱形铁皮容器,底面半径是
3 dm,高是 4 dm,做这个容器至少需要多少
平方分米的铁皮?
思路分析:由于容器没有盖,所以计算表面积时,
底面积只有一个,即容器的表面积等
于侧面积加上一个底面积
规范解答:
容器的侧面积:
2×3.14×3×4=75.36(dm2)
容器的表面积:
75.36+28.26=103.62(dm2)
答:做这个容器至少需要103.62平方分米的铁皮。
考点 3
圆柱的体积
例 3 把一个圆柱的底面平均分成若干个扇形,沿高
切开拼成一个近似的长方体,这个长方体的长
是 6.28 厘米,高是 5 厘米。这个圆柱的体积是
多少立方厘米?(π值取 3.14) ( )
思路分析:应该先求出圆柱的底面周长,再求出底
面半径,最后求出体积。
规范解答:
圆柱的底面半径(长方体的宽):
6.28×2÷3.14÷2=2(厘米)
6.28×2×5=62.8(立方厘米)
答:这个圆柱的体积是62.8立方厘米。
考点 4
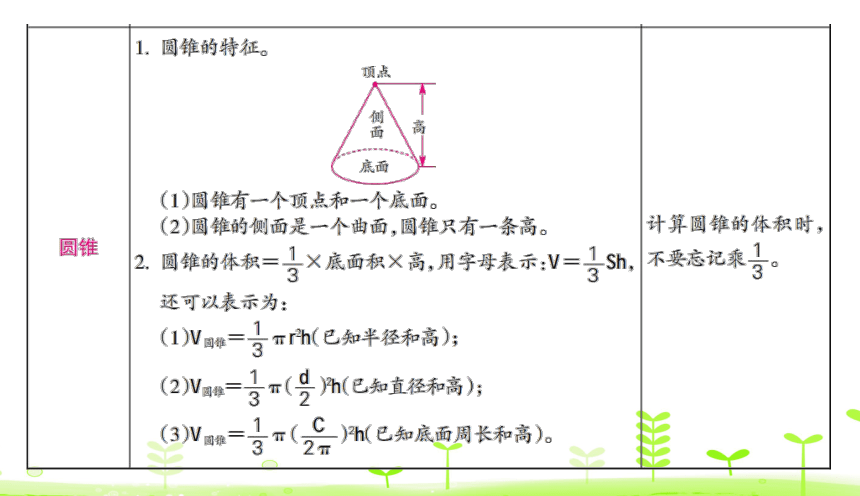
圆锥的体积
例 4 某座塔的顶端近似于圆锥形,它的底面周长
是18.84 m,高是6 m,求塔的顶端的体积。
思路分析:塔的顶端呈圆锥形,求塔的顶端的体积
就是求圆锥的体积。
规范解答:
圆锥的底面积:
3.14×(18.84÷3.14÷2)2
=3.14×9
圆锥的体积:
=28.26(m2)
3
1
×28.26×6
=2×28.26
=56.52(m3)
答:塔的顶端的体积是56.52m3。
36m3=( )dm3
36000
4.28dm3=( )cm3=( )mL
一、填空题。
2.如图 ,以a为轴旋转一周,可以得
到一个( ),a是它的( ),b是它
的( )。
1.
4280
4280
圆锥
高
底面半径
3. 一个圆柱的底面半径是3 cm,高是5 cm,侧面
积是( )cm2,表面积是( )cm2。
94.2
4. 一个圆柱的底面半径是5 dm,高是18 dm,体积
是( )dm3,与它等底等高的圆锥的体积是
( )dm3。
150.72
1413
471
5.一个圆锥底面积是2 cm2,高是5 cm,它的体积
是( )cm3。
6. 一个圆柱的体积是28.26 dm3,底面积是6.28 dm2,
它的高是( )dm。
7. 12 个同样大小的圆锥形铅锭,可以铸成( )
个与它等底等高的圆柱形铅锭。。
4.5
3
8
4
二、判断题。
1.圆柱和圆锥都有无数条高。 ( )
2.将圆锥的侧面展开可以得到一个扇形。( )
3.两个圆锥的底面积相等,则它们的体积也一定相
等。 ( )
4. 一个圆柱的高不变,底面半径扩大到原来的2倍,
体积也扩大到原来的2倍。 ( )
×
√
×
×
三、选择题。
1.油漆5根圆柱形柱子,就是油漆这5根柱子的
( )。
A. 底面积 B. 侧面积 C. 表面积 D. 体积
2.修一个深 2.2m,底面直径是 4m 的圆柱形蓄水
池,这个蓄水池占地( )m2。
A. 12.56 B. 27.632 C. 6.28 D. 3.14
B
A
四、解决问题。
1、一个圆柱形的水池,底面直径是20 m,深是2 m。
水池的占地面积是多少?
(20÷2)2×3.14=314(m2)
答:水池的占地面积是314平方米。
2、一个圆锥形的沙堆,底面积是18平方米,高是
1.5米。如果每立方米的沙子重1.6 吨,那么这堆
沙子重多少吨?
答:那么这堆沙子重14.4吨。
18×1.5× ×1.6=14.4(吨)
3
1
3、小刚家里来了两位客人,妈妈冲了1 L 果汁,如
果用下图中的玻璃杯喝果汁,小刚和客人每人一
满杯够吗?(玻璃杯厚度忽略不计)
(6÷2)2×3.14×12×(2+1)
=1017.36(cm3)
=1.01736(L)
1.01736>1,不够。
答:小刚和客人每人一满杯不够。
整理与复习
考点1
面的旋转
例 1 下面的图形旋转一周,可以得到哪个立体图形?
用线连一连。
思路分析:1. 想象长方形、直角三角形、半圆旋
转后形成的图形。
2. 分别把旋转后形成的图形组合起来,
再连线。
规范解答:
考点 2
圆柱的表面积
例 2 做一个无盖的圆柱形铁皮容器,底面半径是
3 dm,高是 4 dm,做这个容器至少需要多少
平方分米的铁皮?
思路分析:由于容器没有盖,所以计算表面积时,
底面积只有一个,即容器的表面积等
于侧面积加上一个底面积
规范解答:
容器的侧面积:
2×3.14×3×4=75.36(dm2)
容器的表面积:
75.36+28.26=103.62(dm2)
答:做这个容器至少需要103.62平方分米的铁皮。
考点 3
圆柱的体积
例 3 把一个圆柱的底面平均分成若干个扇形,沿高
切开拼成一个近似的长方体,这个长方体的长
是 6.28 厘米,高是 5 厘米。这个圆柱的体积是
多少立方厘米?(π值取 3.14) ( )
思路分析:应该先求出圆柱的底面周长,再求出底
面半径,最后求出体积。
规范解答:
圆柱的底面半径(长方体的宽):
6.28×2÷3.14÷2=2(厘米)
6.28×2×5=62.8(立方厘米)
答:这个圆柱的体积是62.8立方厘米。
考点 4
圆锥的体积
例 4 某座塔的顶端近似于圆锥形,它的底面周长
是18.84 m,高是6 m,求塔的顶端的体积。
思路分析:塔的顶端呈圆锥形,求塔的顶端的体积
就是求圆锥的体积。
规范解答:
圆锥的底面积:
3.14×(18.84÷3.14÷2)2
=3.14×9
圆锥的体积:
=28.26(m2)
3
1
×28.26×6
=2×28.26
=56.52(m3)
答:塔的顶端的体积是56.52m3。
36m3=( )dm3
36000
4.28dm3=( )cm3=( )mL
一、填空题。
2.如图 ,以a为轴旋转一周,可以得
到一个( ),a是它的( ),b是它
的( )。
1.
4280
4280
圆锥
高
底面半径
3. 一个圆柱的底面半径是3 cm,高是5 cm,侧面
积是( )cm2,表面积是( )cm2。
94.2
4. 一个圆柱的底面半径是5 dm,高是18 dm,体积
是( )dm3,与它等底等高的圆锥的体积是
( )dm3。
150.72
1413
471
5.一个圆锥底面积是2 cm2,高是5 cm,它的体积
是( )cm3。
6. 一个圆柱的体积是28.26 dm3,底面积是6.28 dm2,
它的高是( )dm。
7. 12 个同样大小的圆锥形铅锭,可以铸成( )
个与它等底等高的圆柱形铅锭。。
4.5
3
8
4
二、判断题。
1.圆柱和圆锥都有无数条高。 ( )
2.将圆锥的侧面展开可以得到一个扇形。( )
3.两个圆锥的底面积相等,则它们的体积也一定相
等。 ( )
4. 一个圆柱的高不变,底面半径扩大到原来的2倍,
体积也扩大到原来的2倍。 ( )
×
√
×
×
三、选择题。
1.油漆5根圆柱形柱子,就是油漆这5根柱子的
( )。
A. 底面积 B. 侧面积 C. 表面积 D. 体积
2.修一个深 2.2m,底面直径是 4m 的圆柱形蓄水
池,这个蓄水池占地( )m2。
A. 12.56 B. 27.632 C. 6.28 D. 3.14
B
A
四、解决问题。
1、一个圆柱形的水池,底面直径是20 m,深是2 m。
水池的占地面积是多少?
(20÷2)2×3.14=314(m2)
答:水池的占地面积是314平方米。
2、一个圆锥形的沙堆,底面积是18平方米,高是
1.5米。如果每立方米的沙子重1.6 吨,那么这堆
沙子重多少吨?
答:那么这堆沙子重14.4吨。
18×1.5× ×1.6=14.4(吨)
3
1
3、小刚家里来了两位客人,妈妈冲了1 L 果汁,如
果用下图中的玻璃杯喝果汁,小刚和客人每人一
满杯够吗?(玻璃杯厚度忽略不计)
(6÷2)2×3.14×12×(2+1)
=1017.36(cm3)
=1.01736(L)
1.01736>1,不够。
答:小刚和客人每人一满杯不够。
