人教版八年级下册数学 18.2.3 正方形 同步练习题(含答案)
文档属性
| 名称 | 人教版八年级下册数学 18.2.3 正方形 同步练习题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 379.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-21 18:27:48 | ||
图片预览

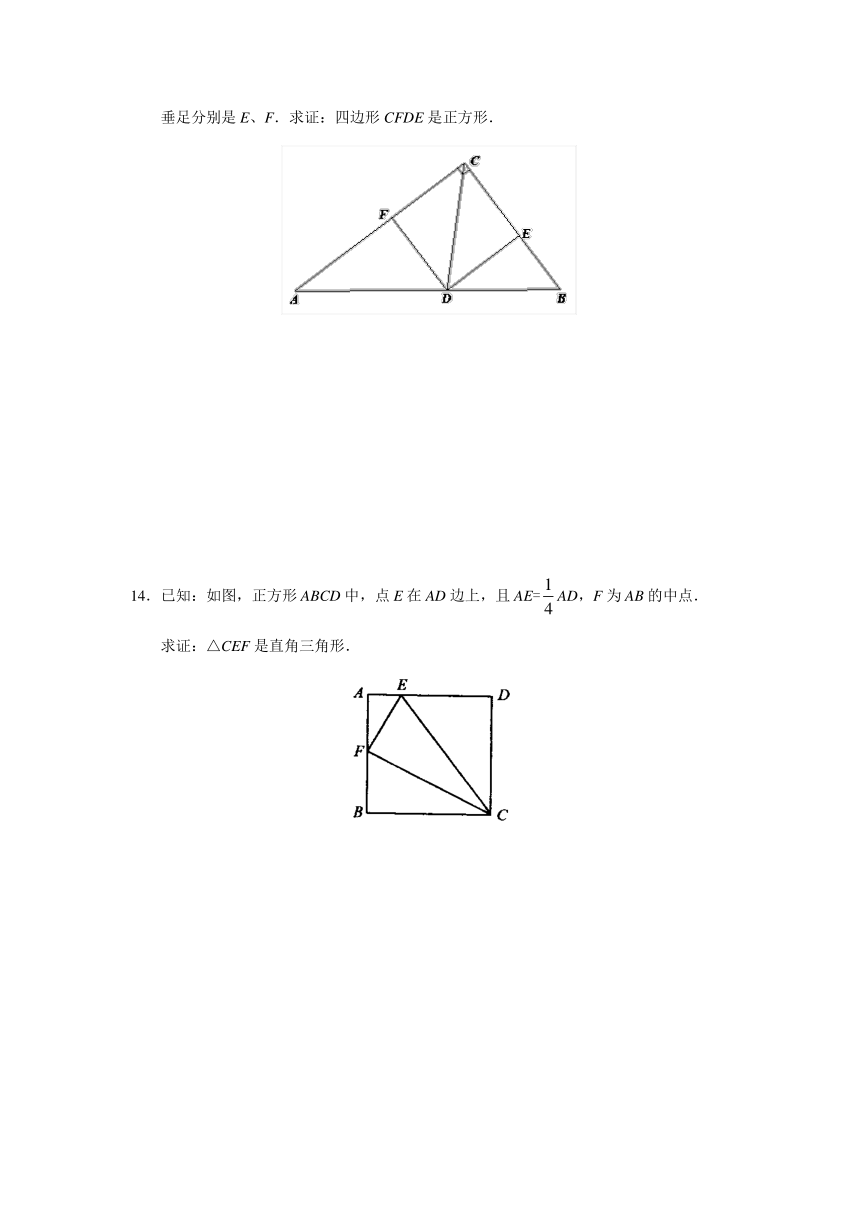
文档简介
18.2.3 正方形 同步练习题
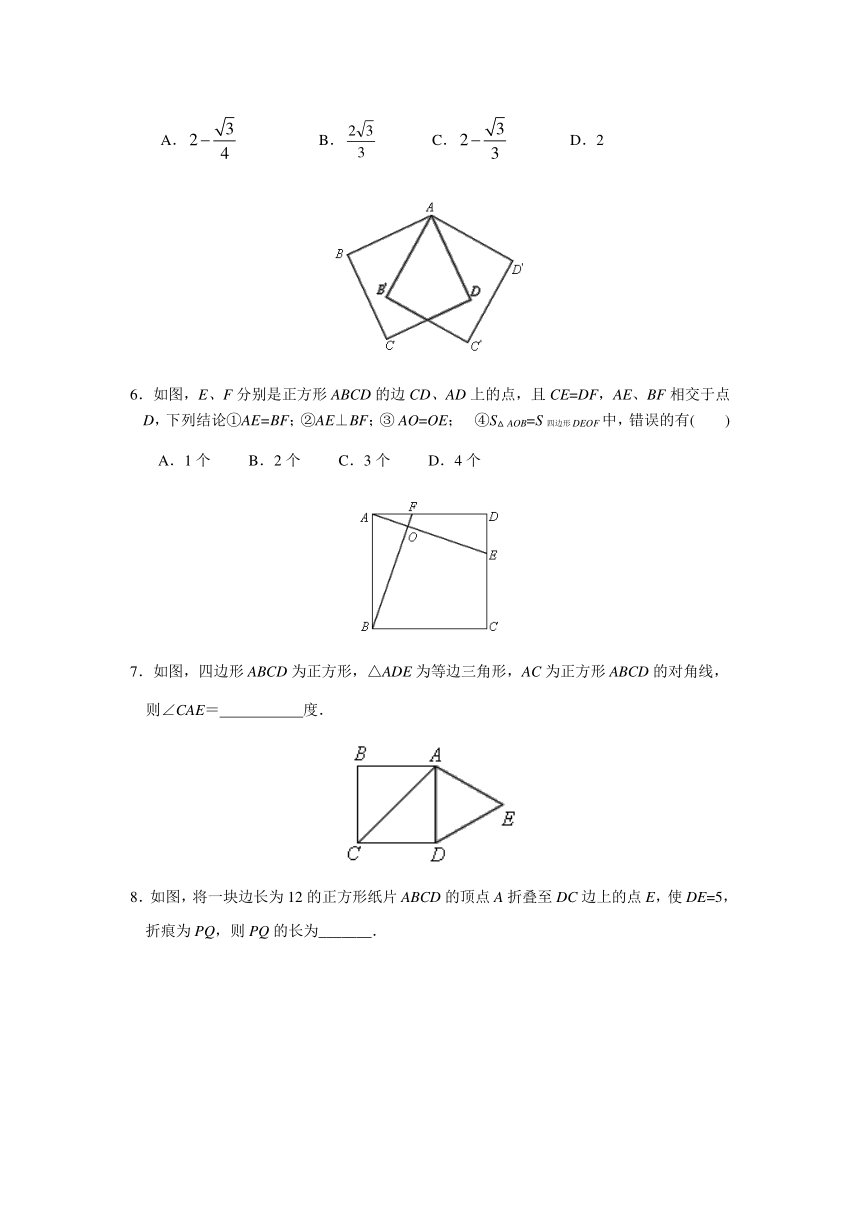
1.如图,阴影部分是一个正方形,则此正方形的面积是( ).
A.8 B.16 C.32 D.64
2.如图,以正方形ABCD的对角线AC为一边作菱形AEFC,则∠FAB等于( )
A.45° B.22.5° C.30° D.135°
3.四边形ABCD的对角线AC、BD相交于点O,能判定它是正方形的是( )
A.OA=OC、OB=OD B.OA=OB=OC=OD
C.OA=OC、OB=OC、AC⊥BD D.OA=OB=OC=OD、AC⊥BD
4.如图,E是边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P是CE上任意一点,PQ⊥BC于Q,PR⊥BE于R,PQ+PR的值是( )
A. B. C. D.
5.边长为1的正方形ABCD绕点A逆时针旋转30°得到正方形AB′C′D′,两图叠成一个“蝶形风筝”(如图所示阴影部分),则这个风筝的面积是( )
A. B. C. D.2
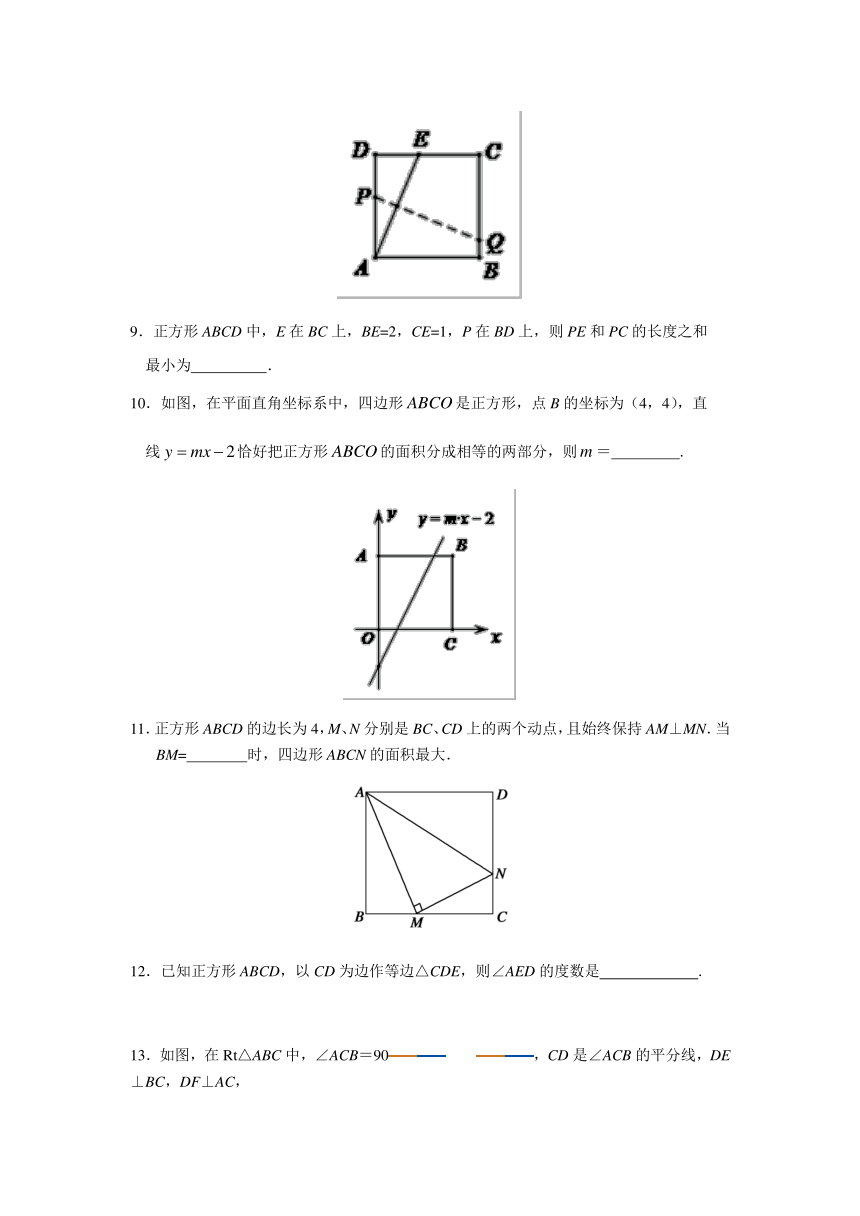
6.如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点D,下列结论①AE=BF;②AE⊥BF;③ AO=OE; ④S△AOB=S四边形DEOF中,错误的有( )
A.1个 B.2个 C.3个 D.4个
7.如图,四边形ABCD为正方形,△ADE为等边三角形,AC为正方形ABCD的对角线,
则∠CAE= 度.
8.如图,将一块边长为12的正方形纸片ABCD的顶点A折叠至DC边上的点E,使DE=5,
折痕为PQ,则PQ的长为_______.
9.正方形ABCD中,E在BC上,BE=2,CE=1,P在BD上,则PE和PC的长度之和
最小为 .
10.如图,在平面直角坐标系中,四边形是正方形,点B的坐标为(4,4),直
线恰好把正方形的面积分成相等的两部分,则= .
11.正方形ABCD的边长为4,M、N分别是BC、CD上的两个动点,且始终保持AM⊥MN.当BM= 时,四边形ABCN的面积最大.
12.已知正方形ABCD,以CD为边作等边△CDE,则∠AED的度数是 .
13.如图,在Rt△ABC中,∠ACB=90,CD是∠ACB的平分线,DE⊥BC,DF⊥AC,
垂足分别是E、F.求证:四边形CFDE是正方形.
14.已知:如图,正方形ABCD中,点E在AD边上,且AE=AD,F为AB的中点.
求证:△CEF是直角三角形.
15.已知,如图,正方形的边长为6,菱形的三个顶点分别在
正方形边上,,连接.
(1)当时,求的面积;
(2)设,用含的代数式表示的面积;
(3)判断的面积能否等于,并说明理由.
16.如图,等腰梯形ABCD中,AD∥BC,点E是线段AD上一个动点(点E与点A,D不重合),
点G,F,H分别是BE,BC,CE的中点.
(1)试探究四边形EGFH的形状,并说明理由;
(2)当点E运动到什么位置时,四边形EGFH是菱形?并加以证明;
(3)如果(2)中的菱形EGFH是正方形,请探索线段EF与线段BC的关系,并证明你的结论.
参考答案
1.D 2.B 3.D 4.A 5.C 6.A
7.105°.
8.13.
9..
10.2.
11.2.
12. 15°或75°.
解析:当点E在正方形ABCD外时,∠AED=15°;
当点E在正方形ABCD内时,∠AED=75°.
13.证明:∵ DE⊥BC,DF⊥AC,∠ACB=90, ∴四边形DFCE为矩形.
又∵CD是∠ACB的平分线,DE⊥BC,DF⊥AC,∴DF=DE.
∴四边形CFDE是正方形.
14.证明:在正方形ABCD中,,.
设,
∵AE=AD,F为AB的中点,
∴,,,.
∵,∴.
同理:,.
∴.∴△CEF是直角三角形.
15.解:(1)在正方形ABCD中,,.
∵正方形的边长为6,,∴.
又∵,∴,即菱形的边长为.
在和中,
,,,
∴.∴.
∵,∴.∴.
∴菱形是正方形.同理可以证明.
∴,即点F在BC边上.
同时可得.∴.
(2)作,M为垂足,连结GE.
∵,∴.
∵,∴.
∴.
又∵,,
∴.∴.
∴无论菱形如何变化,点到直线的距离始终为定值2.
∴.
(3)若,由,得.
此时,在中,.
相应地,在中,,即点已经不在边上.
故不可能有.
16.解:(1)四边形EGFH是平行四边形.
理由:∵G,F分别为BE,BC的中点, ∴GF∥CE .
同理:FH∥BE. ∴四边形EGFH是平行四边形.
(2)当点E是AD的中点时,四边形EGFH是菱形.
证明:∵四边形ABCD是等腰梯形,∴AB=DC,∠A=∠D.
∵AE=DE, ∴△ABE≌△DCE .∴BE=CE.
∵G,H分别为BE,CE的中点,∴GE=HE.
∵四边形EGFH是平行四边形,∴四边形EGFH是菱形.
(3)EF⊥BC,EF=BC.
证明:∵四边形EGFH是正方形,∴EG=EH,∠BEC=90°.
∵G,H分别为BE,CE的中点, ∴BE=CE.
∵F是BC的中点,∴EF⊥BC,EF=BC.
1.如图,阴影部分是一个正方形,则此正方形的面积是( ).
A.8 B.16 C.32 D.64
2.如图,以正方形ABCD的对角线AC为一边作菱形AEFC,则∠FAB等于( )
A.45° B.22.5° C.30° D.135°
3.四边形ABCD的对角线AC、BD相交于点O,能判定它是正方形的是( )
A.OA=OC、OB=OD B.OA=OB=OC=OD
C.OA=OC、OB=OC、AC⊥BD D.OA=OB=OC=OD、AC⊥BD
4.如图,E是边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P是CE上任意一点,PQ⊥BC于Q,PR⊥BE于R,PQ+PR的值是( )
A. B. C. D.
5.边长为1的正方形ABCD绕点A逆时针旋转30°得到正方形AB′C′D′,两图叠成一个“蝶形风筝”(如图所示阴影部分),则这个风筝的面积是( )
A. B. C. D.2
6.如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点D,下列结论①AE=BF;②AE⊥BF;③ AO=OE; ④S△AOB=S四边形DEOF中,错误的有( )
A.1个 B.2个 C.3个 D.4个
7.如图,四边形ABCD为正方形,△ADE为等边三角形,AC为正方形ABCD的对角线,
则∠CAE= 度.
8.如图,将一块边长为12的正方形纸片ABCD的顶点A折叠至DC边上的点E,使DE=5,
折痕为PQ,则PQ的长为_______.
9.正方形ABCD中,E在BC上,BE=2,CE=1,P在BD上,则PE和PC的长度之和
最小为 .
10.如图,在平面直角坐标系中,四边形是正方形,点B的坐标为(4,4),直
线恰好把正方形的面积分成相等的两部分,则= .
11.正方形ABCD的边长为4,M、N分别是BC、CD上的两个动点,且始终保持AM⊥MN.当BM= 时,四边形ABCN的面积最大.
12.已知正方形ABCD,以CD为边作等边△CDE,则∠AED的度数是 .
13.如图,在Rt△ABC中,∠ACB=90,CD是∠ACB的平分线,DE⊥BC,DF⊥AC,
垂足分别是E、F.求证:四边形CFDE是正方形.
14.已知:如图,正方形ABCD中,点E在AD边上,且AE=AD,F为AB的中点.
求证:△CEF是直角三角形.
15.已知,如图,正方形的边长为6,菱形的三个顶点分别在
正方形边上,,连接.
(1)当时,求的面积;
(2)设,用含的代数式表示的面积;
(3)判断的面积能否等于,并说明理由.
16.如图,等腰梯形ABCD中,AD∥BC,点E是线段AD上一个动点(点E与点A,D不重合),
点G,F,H分别是BE,BC,CE的中点.
(1)试探究四边形EGFH的形状,并说明理由;
(2)当点E运动到什么位置时,四边形EGFH是菱形?并加以证明;
(3)如果(2)中的菱形EGFH是正方形,请探索线段EF与线段BC的关系,并证明你的结论.
参考答案
1.D 2.B 3.D 4.A 5.C 6.A
7.105°.
8.13.
9..
10.2.
11.2.
12. 15°或75°.
解析:当点E在正方形ABCD外时,∠AED=15°;
当点E在正方形ABCD内时,∠AED=75°.
13.证明:∵ DE⊥BC,DF⊥AC,∠ACB=90, ∴四边形DFCE为矩形.
又∵CD是∠ACB的平分线,DE⊥BC,DF⊥AC,∴DF=DE.
∴四边形CFDE是正方形.
14.证明:在正方形ABCD中,,.
设,
∵AE=AD,F为AB的中点,
∴,,,.
∵,∴.
同理:,.
∴.∴△CEF是直角三角形.
15.解:(1)在正方形ABCD中,,.
∵正方形的边长为6,,∴.
又∵,∴,即菱形的边长为.
在和中,
,,,
∴.∴.
∵,∴.∴.
∴菱形是正方形.同理可以证明.
∴,即点F在BC边上.
同时可得.∴.
(2)作,M为垂足,连结GE.
∵,∴.
∵,∴.
∴.
又∵,,
∴.∴.
∴无论菱形如何变化,点到直线的距离始终为定值2.
∴.
(3)若,由,得.
此时,在中,.
相应地,在中,,即点已经不在边上.
故不可能有.
16.解:(1)四边形EGFH是平行四边形.
理由:∵G,F分别为BE,BC的中点, ∴GF∥CE .
同理:FH∥BE. ∴四边形EGFH是平行四边形.
(2)当点E是AD的中点时,四边形EGFH是菱形.
证明:∵四边形ABCD是等腰梯形,∴AB=DC,∠A=∠D.
∵AE=DE, ∴△ABE≌△DCE .∴BE=CE.
∵G,H分别为BE,CE的中点,∴GE=HE.
∵四边形EGFH是平行四边形,∴四边形EGFH是菱形.
(3)EF⊥BC,EF=BC.
证明:∵四边形EGFH是正方形,∴EG=EH,∠BEC=90°.
∵G,H分别为BE,CE的中点, ∴BE=CE.
∵F是BC的中点,∴EF⊥BC,EF=BC.
