北师大版八年级数学下册6.1.1平行四边形的性质课件(共23张PPT)
文档属性
| 名称 | 北师大版八年级数学下册6.1.1平行四边形的性质课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-21 22:59:01 | ||
图片预览





文档简介
(共23张PPT)
平行四边形是生活中常见的图形,你能举出一些实例吗?
美观别致
随处可见
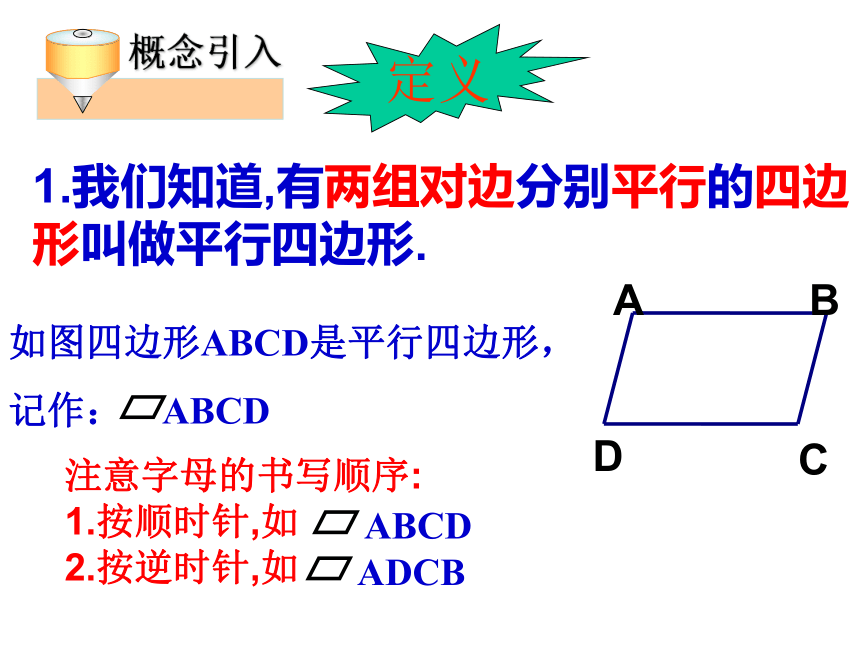
1.我们知道,有两组对边分别平行的四边形叫做平行四边形.
如图四边形ABCD是平行四边形,
注意字母的书写顺序:
1.按顺时针,如
2.按逆时针,如
定义
定义
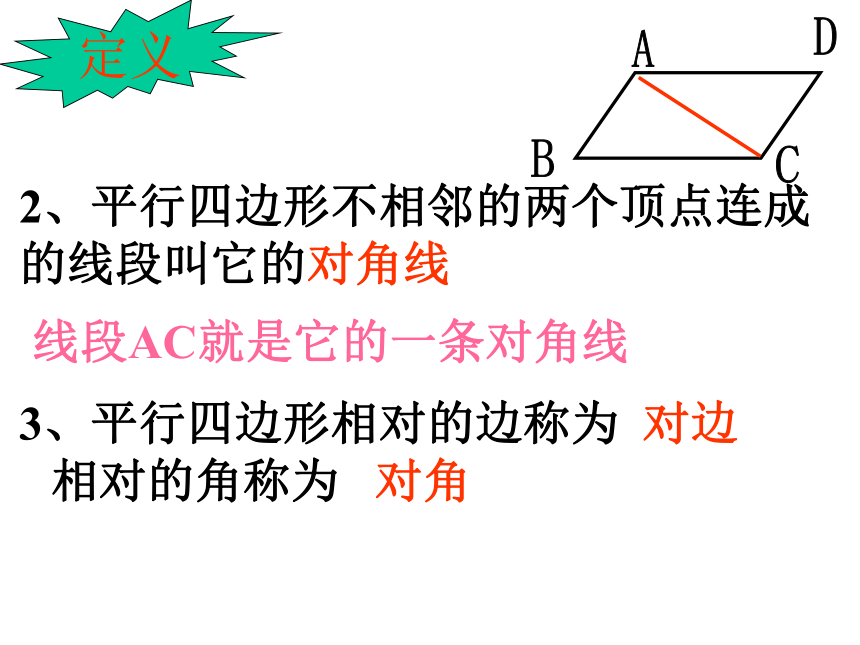
2、平行四边形不相邻的两个顶点连成的线段叫它的对角线
线段AC就是它的一条对角线
3、平行四边形相对的边称为 对边 相对的角称为 对角
平行四边形
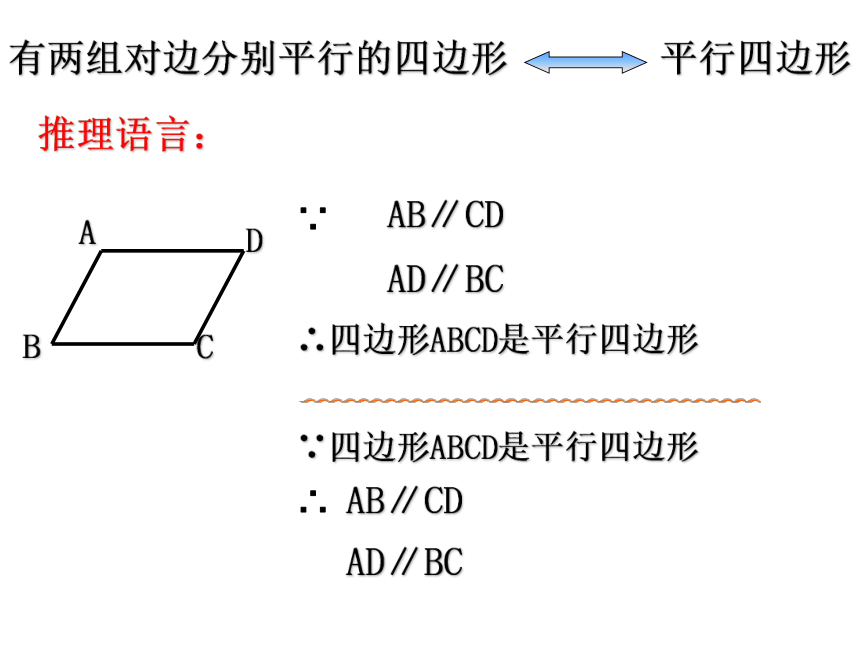
有两组对边分别平行的四边形
推理语言:
∵四边形ABCD是平行四边形
∴四边形ABCD是平行四边形
你能从以下图形中找出平行四边形吗?
两组对边分别平行,是平行四边形的一个主要特征。
除此之外,它还有什么特征呢?
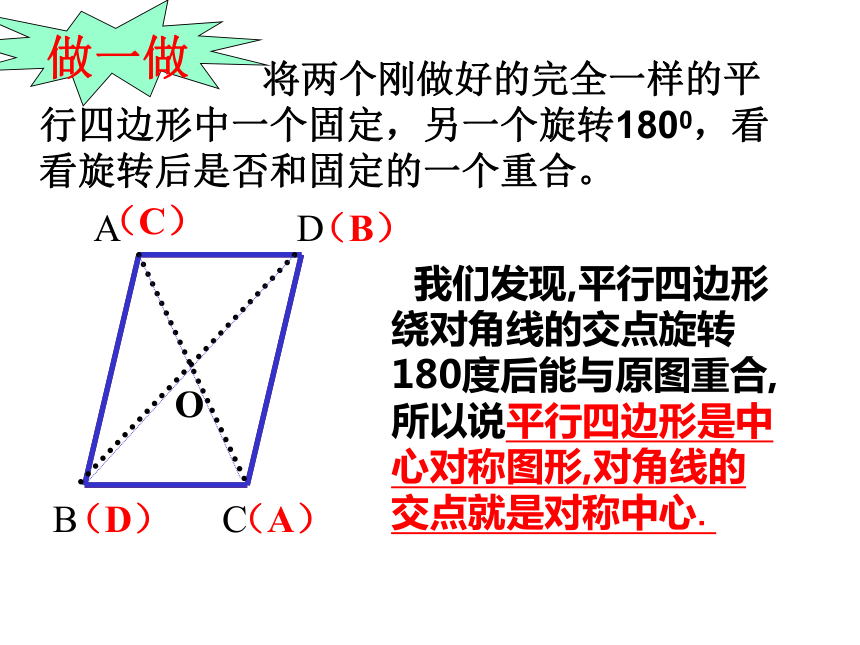
将两个刚做好的完全一样的平行四边形中一个固定,另一个旋转1800,看看旋转后是否和固定的一个重合。
O
A
B
C
D
(C)
(A)
(B)
(D)
做一做
我们发现,平行四边形绕对角线的交点旋转180度后能与原图重合,所以说平行四边形是中心对称图形,对角线的交点就是对称中心.
同桌讨论:观察、猜测平行四边形
有哪些性质?
实验报告:
研究对象
研究结果
几何表示
对边
对角
平行且相等
AB∥CD AD∥BC
AB=CD AD=BC
相等
∠A=∠C ,∠ B=∠D
平行四边形的性质:
性质1:平行四边形的对边相等。
你能证明它们吗?
56°
124°
56°
已知 ABCD中,∠BAD= 56° 则:∠BCD=
124°
56°
124°
124°
∠B =
∴ ∠BAD+ ∠B = 180°
∵ AD∥BC
∠D=
结论:平行四边形的邻角互补
练习1.已知 ABCD中,∠A=120°,
你能求出其余各内角的度数吗?
说说你的理由。
120°
解:在 ABCD中, ∠C=∠ A=120°;
∠B=∠D =180°- ∠A=180°- 120°= 60°
(两直线平行,同旁内角互补)
2.已知 ABCD中,
∠A+∠C=100°,
你能求出各角的度数吗?
说说你的理由。
解:∵在平行四边形ABCD中, ∠A+∠C=100°,
∴ ∠A= ∠C= 50°; ∠B=∠D= 180- 50°= 130°.
A
D
C
B
8
例 如图,已知 中,AB=8,
周长等于24,求其余三条边的长.
解:在 中, AD=BC, CD=AB=8;
因为AD+BC+CD+AB=24,
所以AD+BC=24-CD-AB=24-8-8=8,
所以AD=BC=8/2=4.
应用巩固 深化提高
(1) 已知:如图6-3,在平行四边形ABCD中,
E,F 是对角线AC上的两点,且AE=CF.
求证:BE = DF.
证明:∵四边形ABCD是平行四边形
∴AB = CD
AB // CD
∴∠BAE=∠DCF
又∵AE=CF
∴△BAE≌△DCF
∴BE=DF
练一练:
在 ABCD 中, 已知一个内角的度数是60°,则其余三个内角的度数分别为:
120°、
60°、
120°
已知在 ABCD中,AD+DC=13,求它的周长
A
B
C
D
13
26
总结:平行四边形两邻边的和的两倍等于周长
在平行四边形ABCD中,若AE平分∠DAB,AB=5cm,AD=9cm,则EC=
C
4cm
3
让我们大家一起来想!
A
B
C
画一个平行四边形,第四个点可以在哪儿?
请你为张师傅弹一条墨线,将锯下的这块平行四边形木板分成面积相等的两部分。你有多少种方法?
无数种,这些墨线都过对角线的交点
平行四边形的性质
边
平行四边形的对边平行且相等;
角
平行四边形的邻角互补。
∵四边形ABCD是
∴ AB∥CD, AD∥BC
AB = CD, AD= BC
∵四边形ABCD是
∴ ∠A=∠C, ∠B=∠D
∵ AB∥CD
∴ ∠A+∠D=1800, ∠B+∠C=1800
平行四边形的对角相等;
O
平行四边形是中心对称图形
1、习题6.1第3,4题;
2、相关资料书的习题。
祝你成功!
平行四边形是生活中常见的图形,你能举出一些实例吗?
美观别致
随处可见
1.我们知道,有两组对边分别平行的四边形叫做平行四边形.
如图四边形ABCD是平行四边形,
注意字母的书写顺序:
1.按顺时针,如
2.按逆时针,如
定义
定义
2、平行四边形不相邻的两个顶点连成的线段叫它的对角线
线段AC就是它的一条对角线
3、平行四边形相对的边称为 对边 相对的角称为 对角
平行四边形
有两组对边分别平行的四边形
推理语言:
∵四边形ABCD是平行四边形
∴四边形ABCD是平行四边形
你能从以下图形中找出平行四边形吗?
两组对边分别平行,是平行四边形的一个主要特征。
除此之外,它还有什么特征呢?
将两个刚做好的完全一样的平行四边形中一个固定,另一个旋转1800,看看旋转后是否和固定的一个重合。
O
A
B
C
D
(C)
(A)
(B)
(D)
做一做
我们发现,平行四边形绕对角线的交点旋转180度后能与原图重合,所以说平行四边形是中心对称图形,对角线的交点就是对称中心.
同桌讨论:观察、猜测平行四边形
有哪些性质?
实验报告:
研究对象
研究结果
几何表示
对边
对角
平行且相等
AB∥CD AD∥BC
AB=CD AD=BC
相等
∠A=∠C ,∠ B=∠D
平行四边形的性质:
性质1:平行四边形的对边相等。
你能证明它们吗?
56°
124°
56°
已知 ABCD中,∠BAD= 56° 则:∠BCD=
124°
56°
124°
124°
∠B =
∴ ∠BAD+ ∠B = 180°
∵ AD∥BC
∠D=
结论:平行四边形的邻角互补
练习1.已知 ABCD中,∠A=120°,
你能求出其余各内角的度数吗?
说说你的理由。
120°
解:在 ABCD中, ∠C=∠ A=120°;
∠B=∠D =180°- ∠A=180°- 120°= 60°
(两直线平行,同旁内角互补)
2.已知 ABCD中,
∠A+∠C=100°,
你能求出各角的度数吗?
说说你的理由。
解:∵在平行四边形ABCD中, ∠A+∠C=100°,
∴ ∠A= ∠C= 50°; ∠B=∠D= 180- 50°= 130°.
A
D
C
B
8
例 如图,已知 中,AB=8,
周长等于24,求其余三条边的长.
解:在 中, AD=BC, CD=AB=8;
因为AD+BC+CD+AB=24,
所以AD+BC=24-CD-AB=24-8-8=8,
所以AD=BC=8/2=4.
应用巩固 深化提高
(1) 已知:如图6-3,在平行四边形ABCD中,
E,F 是对角线AC上的两点,且AE=CF.
求证:BE = DF.
证明:∵四边形ABCD是平行四边形
∴AB = CD
AB // CD
∴∠BAE=∠DCF
又∵AE=CF
∴△BAE≌△DCF
∴BE=DF
练一练:
在 ABCD 中, 已知一个内角的度数是60°,则其余三个内角的度数分别为:
120°、
60°、
120°
已知在 ABCD中,AD+DC=13,求它的周长
A
B
C
D
13
26
总结:平行四边形两邻边的和的两倍等于周长
在平行四边形ABCD中,若AE平分∠DAB,AB=5cm,AD=9cm,则EC=
C
4cm
3
让我们大家一起来想!
A
B
C
画一个平行四边形,第四个点可以在哪儿?
请你为张师傅弹一条墨线,将锯下的这块平行四边形木板分成面积相等的两部分。你有多少种方法?
无数种,这些墨线都过对角线的交点
平行四边形的性质
边
平行四边形的对边平行且相等;
角
平行四边形的邻角互补。
∵四边形ABCD是
∴ AB∥CD, AD∥BC
AB = CD, AD= BC
∵四边形ABCD是
∴ ∠A=∠C, ∠B=∠D
∵ AB∥CD
∴ ∠A+∠D=1800, ∠B+∠C=1800
平行四边形的对角相等;
O
平行四边形是中心对称图形
1、习题6.1第3,4题;
2、相关资料书的习题。
祝你成功!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
