人教版九年级下册28.2解直角三角形及其应用复习课件(23张PPT)
文档属性
| 名称 | 人教版九年级下册28.2解直角三角形及其应用复习课件(23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-21 22:46:46 | ||
图片预览


文档简介
(共23张PPT)
松滋市网络直播课
松滋市九年级 数学
主播:松滋市八宝中学 李万敏
35. 解直角三角形
35. 解直角三角形
以点带面
1
典例精析
2
考点突破
3
4
以点带面
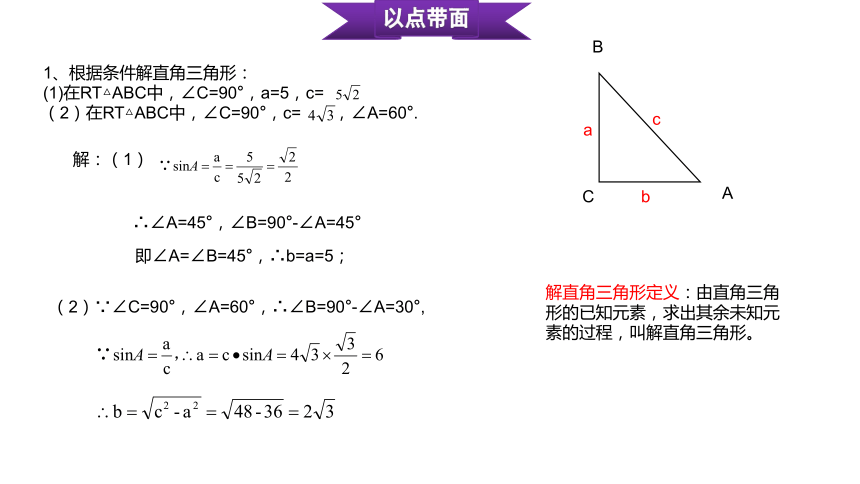
1、根据条件解直角三角形:
(1)在RT△ABC中,∠C=90°,a=5,c=
(2)在RT△ABC中,∠C=90°,c= ,∠A=60°.
解:(1)
C
A
B
c
b
a
∴∠A=45°,∠B=90°-∠A=45°
即∠A=∠B=45°,∴b=a=5;
(2)∵∠C=90°,∠A=60°,∴∠B=90°-∠A=30°,
解直角三角形定义:由直角三角形的已知元素,求出其余未知元素的过程,叫解直角三角形。
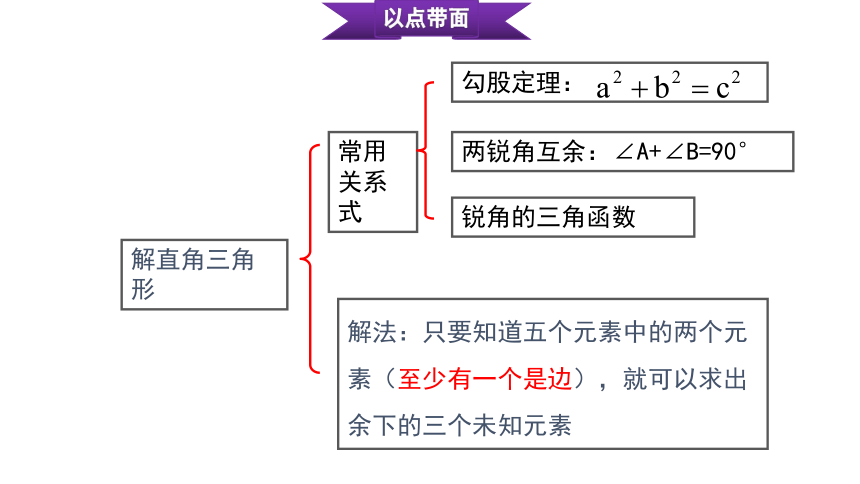
解直角三角形
常用关系式
解法:只要知道五个元素中的两个元素(至少有一个是边),就可以求出余下的三个未知元素
勾股定理:
两锐角互余:∠A+∠B=90°
锐角的三角函数
以点带面
以点带面
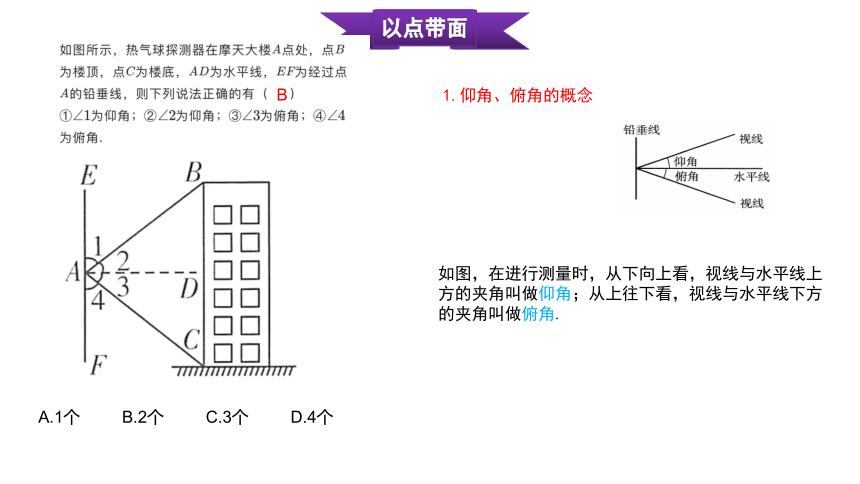
A.1个 B.2个 C.3个 D.4个
B
1.仰角、俯角的概念
如图,在进行测量时,从下向上看,视线与水平线上方的夹角叫做仰角;从上往下看,视线与水平线下方的夹角叫做俯角.
以点带面
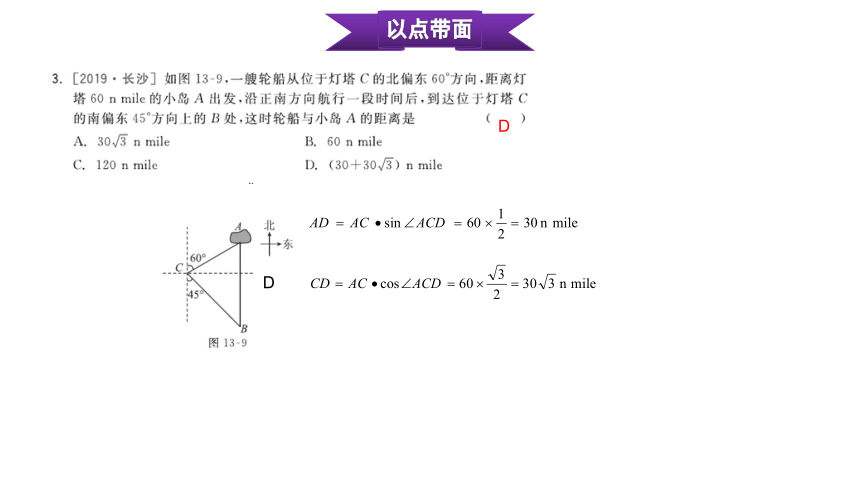
D
D
以点带面
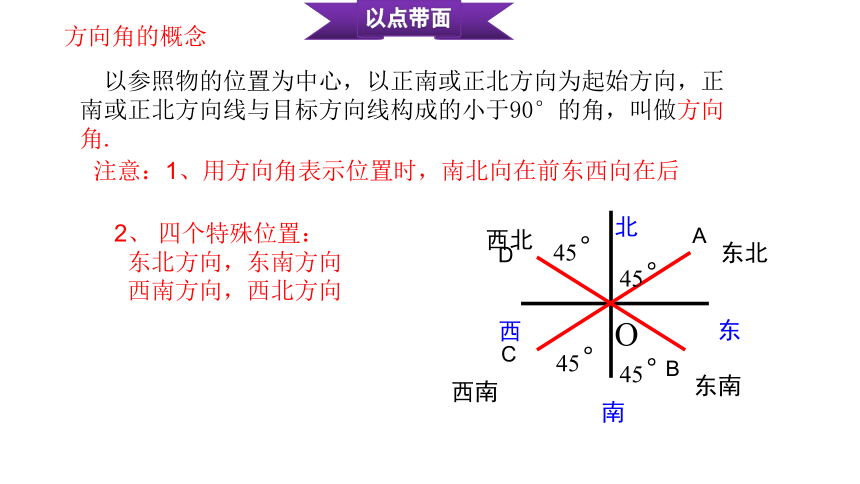
以参照物的位置为中心,以正南或正北方向为起始方向,正南或正北方向线与目标方向线构成的小于90°的角,叫做方向角.
注意:1、用方向角表示位置时,南北向在前东西向在后
2、 四个特殊位置:
东北方向,东南方向
西南方向,西北方向
45°
45°
45°
西南
O
东北
东
西
北
南
西北
东南
45°
C
B
D
A
方向角的概念
以点带面
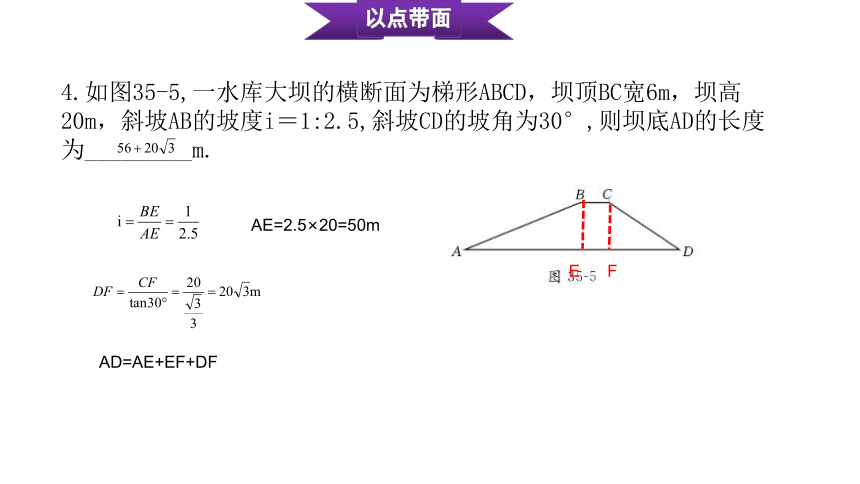
4.如图35-5,一水库大坝的横断面为梯形ABCD,坝顶BC宽6m,坝高20m,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30°,则坝底AD的长度为_________m.
E
F
AE=2.5×20=50m
AD=AE+EF+DF
α
l
h
i= h : l
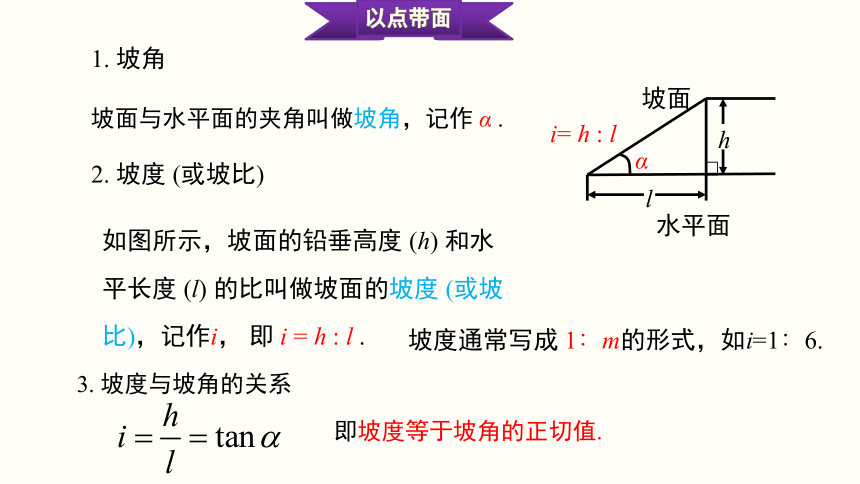
1. 坡角
坡面与水平面的夹角叫做坡角,记作 α .
2. 坡度 (或坡比)
坡度通常写成 1∶m的形式,如i=1∶6.
如图所示,坡面的铅垂高度 (h) 和水
平长度 (l) 的比叫做坡面的坡度 (或坡
比),记作i, 即 i = h : l .
坡面
水平面
以点带面
3. 坡度与坡角的关系
即坡度等于坡角的正切值.
例1、如图35-1,在Rt△ABC中,∠C=90°, 点D是AC边上一点,tan∠DBC= ,且BC=6,AD=4,求cosA的值.
6
4
解:在RT△BDC中,∠C=90°,BC=6,
∴ CD=8
∴AC=AD+DC=4+8=12.
在RT△ABC中,由勾股定理得
分析:先求DC的长,然后根据AC=AD+DC即可求出AC,再根据勾股定理求AB,最后求cosA即可.
典例精析
解直角三角形的应用中的模型:“双直角三角形”。所谓“双直角三角形”是指一条直角边重合,另一条直角边共线的两个直角三角形。其位置关系有两种:
叠合式
背靠式
解决这类问题时,抓住两三角形的公共边,并找到公共边与其它相关边的关系,直接计算或列方程解决问题.
方法小结
2、.如图35-8所示,小敏同学测量一建筑物CD的高度,她站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走30m,到达点F处测得楼顶C的仰角为45°(B、F、D在同一直线上),已知小敏的眼睛与地面距离为1.5m,求这栋建筑物CD的高度.
解法:理解为“异地双仰”
设CG=x
G
你能寻找其中的等量关系列方程吗
AE=AG-EG
解:延长AE交CD于G,设CG=xm,
在RT△CGE中,∠CGE=45°,则EG=CG=xm
∵ AE=AG-EG
则CD=CG+GD=40.98+1.5=42.48≈42m
答:这栋建筑物CD的高度约为42m
典例精析
典例精析
【变式】小敏同学测量一建筑物CD的高度,大楼AB的高为27m,她在楼顶B处测得塔顶D的仰角为30°,塔底C点的俯角为45°,则建筑物CD的高度为多少米?(人的身高忽略不计)
B
D
解法:理解为“高地仰俯”
E
求建筑物CD高度,先找哪些是可解直角三角形?哪些是可表直角三角形?
解:过B作BE⊥CD于E,
∵AB=27m,∴CE=27m.
在RT△BCE中,∠CBE=45°,∴BE=CE=27m
在RT△BDE中,∠DBE=30°,
【变式】小敏同学测量一建筑物CD的高度,大楼AB的高为m,她在楼顶A处测得塔顶D的仰角为α,BC的长度为n,则建筑物CD的高度为多少?(人的身高忽略不计)
典例精析
高地单仰
【变式】小敏同学测量山顶铁塔CD的高度,她站在A处测得D点的仰角的β,C点的仰角为α,已知AB=m,则铁塔CD的高度为多少?(人的身高忽略不计)
同地双仰
典例精析
模型一:高地单仰
模型三:同地双仰
模型二:高地仰俯
模型四:异地双仰
仰角、俯角问题的基本模型多,并不复杂,如:求建筑物CD高度,先找哪些是可解直角三角形?哪些是可表直角三角形?(图中仅有x为未知边,其余均为已知量)
典例精析
例3、.如图35-9所示,A、B、C三地在同一直线上,D地在A地北偏东45°方向,在B地正北方向,在C地北偏西60°方向.C地在A地北偏东75°方向.B、D两地相距2km.问从A地到B地再到C地最后到D地的总路程大约是多少千米?(最后结果保留整数,参考数据: )
解:过B作BE⊥AD于点M,过B作BF⊥DC于点N.
450
600
B
C
A
D
F
E
M
N
由题意得AE∥BD∥CF,
∴∠ADB=∠EAD=45°,∠BDC=∠DCF=60°
∠EAC+∠ABC=180°,∠BCD=180°-75°-60°=45°
∠DAB=∠EAB-∠EAD=75°-45°=30°
典例精析
解决一般三角形的问题,可以通过作高线,构造特殊直角三角形
(1)把实际问题转化为数学问题,这个转化为两个方面:一是将实际问题转化为几何图形,画出正确的平面图或截面示意图,二是将已知条件转化为示意图中的边、角或它们之间的关系。
(2)把数学问题转化为解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,画出直角三角形。
方法小结
考点突破
(1).如图35-3,已知AD是等腰△ABC底边BC上的高,sinB= ,点E在AC上,且AE:EC=2:3,则tan∠ADE的值为( )A. B. C. D.
解:设AD=4x,则AB=5x,BD=3x
DC=3x
∵EF∥DC
F
B
参数法解直角三角形
考点突破
(2).如图35-7,在Rt△ABC中,∠C=90°,∠CAB、∠B、∠C的对边分别为a、b、c,且b= ,AD平分∠CAB的平分线交CB于点D,AD= ,则BC=___________, AB=____________.
∠CAD=30°
分析:先根据三角函数值可求出∠CAD的度数,再根据角平分线的定义可求出∠CAB的度数,再根据三角函数可求解,要熟练掌握边角之间的关系。
考点突破
(3).(2017·荆州中考)如图,某数学活动小组为测量学校旗杆AB的高度,沿旗杆正前方 米处的点C出发,沿斜面坡度i=1∶ 的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A,B,C,D,E在同一平面内,AB⊥BC,AB∥DE,求旗杆AB的高度(参考数据:sin37°≈ ,cos37°≈ ,tan37°≈ .计算结果保留根号).
4
1.5
F
G
解:如图,延长ED交BC的延长线于点F,则∠CFD=90°
过点E作EG⊥AB于点G,则GE=BF=
GB=EF=ED+DF=1.5+2=3.5m
解直角三角形
定义:由直角三角形的已知元素,求出其余未知元素的过程,叫解直角三角形。
应用举例
常用关系式
∠A+∠B=90°
边角之间的关系
仰角、俯角问题
方向角问题
坡度、坡角问题
课堂小结
作业:
1,整理笔记,纠正错题
2,提前做《学在荆州》81-82面
松滋市网络直播课
松滋市九年级 数学
主播:松滋市八宝中学 李万敏
35. 解直角三角形
35. 解直角三角形
以点带面
1
典例精析
2
考点突破
3
4
以点带面
1、根据条件解直角三角形:
(1)在RT△ABC中,∠C=90°,a=5,c=
(2)在RT△ABC中,∠C=90°,c= ,∠A=60°.
解:(1)
C
A
B
c
b
a
∴∠A=45°,∠B=90°-∠A=45°
即∠A=∠B=45°,∴b=a=5;
(2)∵∠C=90°,∠A=60°,∴∠B=90°-∠A=30°,
解直角三角形定义:由直角三角形的已知元素,求出其余未知元素的过程,叫解直角三角形。
解直角三角形
常用关系式
解法:只要知道五个元素中的两个元素(至少有一个是边),就可以求出余下的三个未知元素
勾股定理:
两锐角互余:∠A+∠B=90°
锐角的三角函数
以点带面
以点带面
A.1个 B.2个 C.3个 D.4个
B
1.仰角、俯角的概念
如图,在进行测量时,从下向上看,视线与水平线上方的夹角叫做仰角;从上往下看,视线与水平线下方的夹角叫做俯角.
以点带面
D
D
以点带面
以参照物的位置为中心,以正南或正北方向为起始方向,正南或正北方向线与目标方向线构成的小于90°的角,叫做方向角.
注意:1、用方向角表示位置时,南北向在前东西向在后
2、 四个特殊位置:
东北方向,东南方向
西南方向,西北方向
45°
45°
45°
西南
O
东北
东
西
北
南
西北
东南
45°
C
B
D
A
方向角的概念
以点带面
4.如图35-5,一水库大坝的横断面为梯形ABCD,坝顶BC宽6m,坝高20m,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30°,则坝底AD的长度为_________m.
E
F
AE=2.5×20=50m
AD=AE+EF+DF
α
l
h
i= h : l
1. 坡角
坡面与水平面的夹角叫做坡角,记作 α .
2. 坡度 (或坡比)
坡度通常写成 1∶m的形式,如i=1∶6.
如图所示,坡面的铅垂高度 (h) 和水
平长度 (l) 的比叫做坡面的坡度 (或坡
比),记作i, 即 i = h : l .
坡面
水平面
以点带面
3. 坡度与坡角的关系
即坡度等于坡角的正切值.
例1、如图35-1,在Rt△ABC中,∠C=90°, 点D是AC边上一点,tan∠DBC= ,且BC=6,AD=4,求cosA的值.
6
4
解:在RT△BDC中,∠C=90°,BC=6,
∴ CD=8
∴AC=AD+DC=4+8=12.
在RT△ABC中,由勾股定理得
分析:先求DC的长,然后根据AC=AD+DC即可求出AC,再根据勾股定理求AB,最后求cosA即可.
典例精析
解直角三角形的应用中的模型:“双直角三角形”。所谓“双直角三角形”是指一条直角边重合,另一条直角边共线的两个直角三角形。其位置关系有两种:
叠合式
背靠式
解决这类问题时,抓住两三角形的公共边,并找到公共边与其它相关边的关系,直接计算或列方程解决问题.
方法小结
2、.如图35-8所示,小敏同学测量一建筑物CD的高度,她站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走30m,到达点F处测得楼顶C的仰角为45°(B、F、D在同一直线上),已知小敏的眼睛与地面距离为1.5m,求这栋建筑物CD的高度.
解法:理解为“异地双仰”
设CG=x
G
你能寻找其中的等量关系列方程吗
AE=AG-EG
解:延长AE交CD于G,设CG=xm,
在RT△CGE中,∠CGE=45°,则EG=CG=xm
∵ AE=AG-EG
则CD=CG+GD=40.98+1.5=42.48≈42m
答:这栋建筑物CD的高度约为42m
典例精析
典例精析
【变式】小敏同学测量一建筑物CD的高度,大楼AB的高为27m,她在楼顶B处测得塔顶D的仰角为30°,塔底C点的俯角为45°,则建筑物CD的高度为多少米?(人的身高忽略不计)
B
D
解法:理解为“高地仰俯”
E
求建筑物CD高度,先找哪些是可解直角三角形?哪些是可表直角三角形?
解:过B作BE⊥CD于E,
∵AB=27m,∴CE=27m.
在RT△BCE中,∠CBE=45°,∴BE=CE=27m
在RT△BDE中,∠DBE=30°,
【变式】小敏同学测量一建筑物CD的高度,大楼AB的高为m,她在楼顶A处测得塔顶D的仰角为α,BC的长度为n,则建筑物CD的高度为多少?(人的身高忽略不计)
典例精析
高地单仰
【变式】小敏同学测量山顶铁塔CD的高度,她站在A处测得D点的仰角的β,C点的仰角为α,已知AB=m,则铁塔CD的高度为多少?(人的身高忽略不计)
同地双仰
典例精析
模型一:高地单仰
模型三:同地双仰
模型二:高地仰俯
模型四:异地双仰
仰角、俯角问题的基本模型多,并不复杂,如:求建筑物CD高度,先找哪些是可解直角三角形?哪些是可表直角三角形?(图中仅有x为未知边,其余均为已知量)
典例精析
例3、.如图35-9所示,A、B、C三地在同一直线上,D地在A地北偏东45°方向,在B地正北方向,在C地北偏西60°方向.C地在A地北偏东75°方向.B、D两地相距2km.问从A地到B地再到C地最后到D地的总路程大约是多少千米?(最后结果保留整数,参考数据: )
解:过B作BE⊥AD于点M,过B作BF⊥DC于点N.
450
600
B
C
A
D
F
E
M
N
由题意得AE∥BD∥CF,
∴∠ADB=∠EAD=45°,∠BDC=∠DCF=60°
∠EAC+∠ABC=180°,∠BCD=180°-75°-60°=45°
∠DAB=∠EAB-∠EAD=75°-45°=30°
典例精析
解决一般三角形的问题,可以通过作高线,构造特殊直角三角形
(1)把实际问题转化为数学问题,这个转化为两个方面:一是将实际问题转化为几何图形,画出正确的平面图或截面示意图,二是将已知条件转化为示意图中的边、角或它们之间的关系。
(2)把数学问题转化为解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,画出直角三角形。
方法小结
考点突破
(1).如图35-3,已知AD是等腰△ABC底边BC上的高,sinB= ,点E在AC上,且AE:EC=2:3,则tan∠ADE的值为( )A. B. C. D.
解:设AD=4x,则AB=5x,BD=3x
DC=3x
∵EF∥DC
F
B
参数法解直角三角形
考点突破
(2).如图35-7,在Rt△ABC中,∠C=90°,∠CAB、∠B、∠C的对边分别为a、b、c,且b= ,AD平分∠CAB的平分线交CB于点D,AD= ,则BC=___________, AB=____________.
∠CAD=30°
分析:先根据三角函数值可求出∠CAD的度数,再根据角平分线的定义可求出∠CAB的度数,再根据三角函数可求解,要熟练掌握边角之间的关系。
考点突破
(3).(2017·荆州中考)如图,某数学活动小组为测量学校旗杆AB的高度,沿旗杆正前方 米处的点C出发,沿斜面坡度i=1∶ 的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A,B,C,D,E在同一平面内,AB⊥BC,AB∥DE,求旗杆AB的高度(参考数据:sin37°≈ ,cos37°≈ ,tan37°≈ .计算结果保留根号).
4
1.5
F
G
解:如图,延长ED交BC的延长线于点F,则∠CFD=90°
过点E作EG⊥AB于点G,则GE=BF=
GB=EF=ED+DF=1.5+2=3.5m
解直角三角形
定义:由直角三角形的已知元素,求出其余未知元素的过程,叫解直角三角形。
应用举例
常用关系式
∠A+∠B=90°
边角之间的关系
仰角、俯角问题
方向角问题
坡度、坡角问题
课堂小结
作业:
1,整理笔记,纠正错题
2,提前做《学在荆州》81-82面
