六年级下册数学课件-第4单元 正比例与反比例 整理与复习 北师大版 (共22张PPT)
文档属性
| 名称 | 六年级下册数学课件-第4单元 正比例与反比例 整理与复习 北师大版 (共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 950.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-22 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
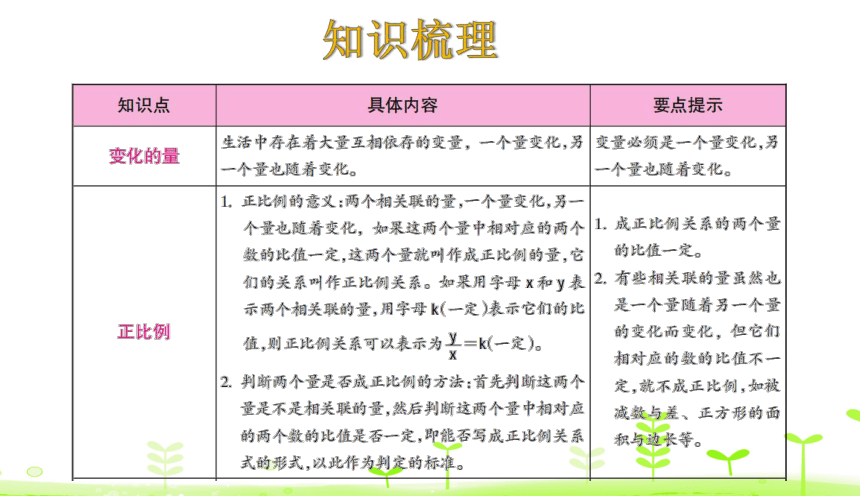
整理与复习
考点1
变化的量
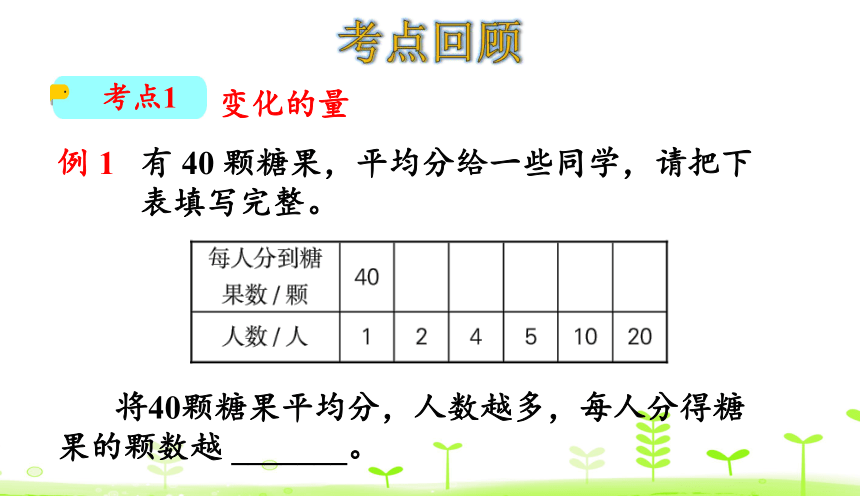
例 1 有 40 颗糖果,平均分给一些同学,请把下
表填写完整。
将40颗糖果平均分,人数越多,每人分得糖果的颗数越 _______。
规范解答:
思路分析:糖果的总颗数一定,则每人分到的糖果
颗数与人数存在以下关系:每人分到糖
果的颗数随人数的增多而减少。
依次填入 20,10,8,4,2将 40 颗糖果平均分,人数越多,每人分得糖果的颗数越少。
考点 2
正比例
例 2 轮船行驶的速度一定,行驶的路程和时间是
不是成正比例关系?
思路分析:判断路程与时间是不是成正比例关系,
先判断路程与时间是不是两种相关联的
量(即是不是一种量变化,另一种量也
随着变化),再看看它们的比值是不是
一定的。
规范解答:
轮船行驶的路程是随着时间的变化而变化的,路程和时间是两种相关联的量,并且“路程÷时间=速度”。
这里速度一定,也就是轮船行驶的路程和时间的比值是一定的,所以轮船行驶的路程和时间成正比例关系。
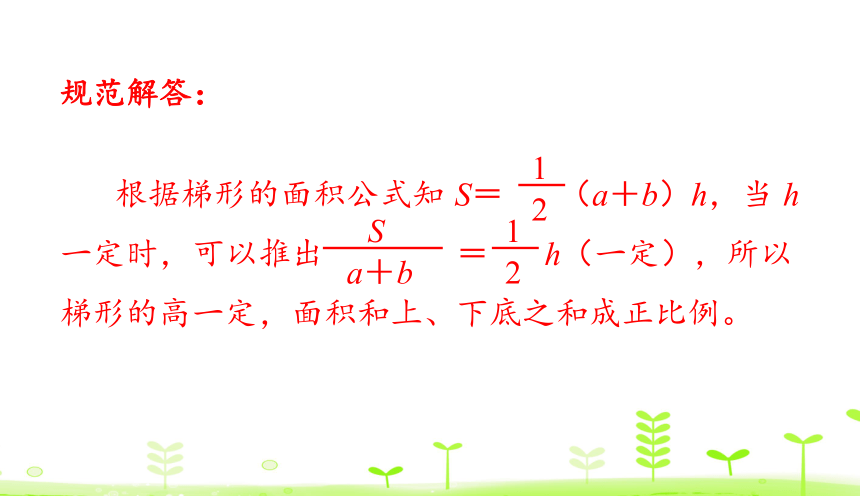
例 3 梯形的高一定,面积和哪种量成正比例?
思路分析:要判断面积和哪种量成正比例,就要看
梯形的高一定时,面积和哪种量的比值
一定。
规范解答:
2
1
根据梯形的面积公式知 S= (a+b)h,当 h 一定时,可以推出 = h(一定),所以梯形的高一定,面积和上、下底之和成正比例。
a+b
S
2
1
考点 3
画一画
例 3 根据所提供的信息先将下表和下图补充完整,
再回答问题。
(1)表中有哪两种变化的量?
(2)香皂的总价与香皂的块数是否成正比例?
为什么?
(3)图中点的连线有什么特点?
(4)如果买15 块香皂,那么需要多少钱?
(5)王阿姨带了20 元钱去买香皂,可以
买多少块?
思路分析:可以先根据“单价×数量=总价”进行计算,
求出总价,再根据香皂的块数与总价的变化情
况得出两种量的关系,最后可以根据总价÷数
量=单价(定值)求出相应的量,也可以借助
图象得出结果。
规范解答:
(1)香皂块数与总价。
(2)成正比例,因为总价÷数量=单价(一定)。
(3)所有的点都在同一条直线上。
(4)15×5=75(元)
答:需要75元。
(5)20÷5=4(块)
答:可以买4块。
考点 4
反比例
例 6 当行驶的路程一定时,车轮的直径和它转动
的圈数是否成反比例?为什么?
思路分析:车轮的直径乘圆周率等于车轮的周长,
即车轮转动一圈的长度。行驶的路程一
定,圆周率一定,那么它们的比值也就
是一定的,所以车轮的直径和车轮转动
的圈数成反比例。
规范解答:
成反比例,因为车轮的直径×车轮转动的圈数= (一定),所以车轮的直径和它转动的圈数成反比例。
圆周率
行驶的路程
成正比例的两个量在变化时的规律是它们的( )不变;成反比例的两个量在变化
时的规律是它们的( )不变。
一、填空题。
2.分子一定,分母和分数值成( )比例;
分母一定,分子和分数值成( )比例。
1.
比值
乘积
反
正
3. 车轮的直径一定,所行的路程和车轮的转数成
( )比例。
正
4. 工作总量一定,工作时间和工作效率成( )
比例。
反
5.修一条路,每天修的米数和需要的天数成
( )比例。
6. 已知x和y的关系是正比例关系,根据表中条件,
填写下表。
反
2
18
24
24
二、判断题。
1.正比例的图象呈一条直线,反比例的图象
呈一条曲线。 ( )
2.被减数一定,减数和差成反比例。 ( )
3.每天做题的数量一定,做题的总数量和天
数成正比例。 ( )
4. 生产效率一定,生产的总量和生产的时间
成反比例。 ( )
√
×
×
√
三、选择题。
1.飞机的速度一定,飞行的时间与路程( )。
A. 成正比例 B. 成反比例 C. 不成比例
2.下列说法中,正确的是( )。
A. 图上距离和实际距离成反比例
A
C
B. 三角形的面积一定,底和对应的高成正比例
C. 正方体的棱长总和与它的棱长成正比例
四、判断下面各题中的两个量是否成比例?如果
成比例,成什么比例,并说明理由。
1、长方体的体积一定,它的底面积和高。
成反比例,因为底面积和高的乘积即长方体的体积一定。
2、除数一定,被除数和商。
成正比例,因为被除数和商的比值也就是除数一定。
整理与复习
考点1
变化的量
例 1 有 40 颗糖果,平均分给一些同学,请把下
表填写完整。
将40颗糖果平均分,人数越多,每人分得糖果的颗数越 _______。
规范解答:
思路分析:糖果的总颗数一定,则每人分到的糖果
颗数与人数存在以下关系:每人分到糖
果的颗数随人数的增多而减少。
依次填入 20,10,8,4,2将 40 颗糖果平均分,人数越多,每人分得糖果的颗数越少。
考点 2
正比例
例 2 轮船行驶的速度一定,行驶的路程和时间是
不是成正比例关系?
思路分析:判断路程与时间是不是成正比例关系,
先判断路程与时间是不是两种相关联的
量(即是不是一种量变化,另一种量也
随着变化),再看看它们的比值是不是
一定的。
规范解答:
轮船行驶的路程是随着时间的变化而变化的,路程和时间是两种相关联的量,并且“路程÷时间=速度”。
这里速度一定,也就是轮船行驶的路程和时间的比值是一定的,所以轮船行驶的路程和时间成正比例关系。
例 3 梯形的高一定,面积和哪种量成正比例?
思路分析:要判断面积和哪种量成正比例,就要看
梯形的高一定时,面积和哪种量的比值
一定。
规范解答:
2
1
根据梯形的面积公式知 S= (a+b)h,当 h 一定时,可以推出 = h(一定),所以梯形的高一定,面积和上、下底之和成正比例。
a+b
S
2
1
考点 3
画一画
例 3 根据所提供的信息先将下表和下图补充完整,
再回答问题。
(1)表中有哪两种变化的量?
(2)香皂的总价与香皂的块数是否成正比例?
为什么?
(3)图中点的连线有什么特点?
(4)如果买15 块香皂,那么需要多少钱?
(5)王阿姨带了20 元钱去买香皂,可以
买多少块?
思路分析:可以先根据“单价×数量=总价”进行计算,
求出总价,再根据香皂的块数与总价的变化情
况得出两种量的关系,最后可以根据总价÷数
量=单价(定值)求出相应的量,也可以借助
图象得出结果。
规范解答:
(1)香皂块数与总价。
(2)成正比例,因为总价÷数量=单价(一定)。
(3)所有的点都在同一条直线上。
(4)15×5=75(元)
答:需要75元。
(5)20÷5=4(块)
答:可以买4块。
考点 4
反比例
例 6 当行驶的路程一定时,车轮的直径和它转动
的圈数是否成反比例?为什么?
思路分析:车轮的直径乘圆周率等于车轮的周长,
即车轮转动一圈的长度。行驶的路程一
定,圆周率一定,那么它们的比值也就
是一定的,所以车轮的直径和车轮转动
的圈数成反比例。
规范解答:
成反比例,因为车轮的直径×车轮转动的圈数= (一定),所以车轮的直径和它转动的圈数成反比例。
圆周率
行驶的路程
成正比例的两个量在变化时的规律是它们的( )不变;成反比例的两个量在变化
时的规律是它们的( )不变。
一、填空题。
2.分子一定,分母和分数值成( )比例;
分母一定,分子和分数值成( )比例。
1.
比值
乘积
反
正
3. 车轮的直径一定,所行的路程和车轮的转数成
( )比例。
正
4. 工作总量一定,工作时间和工作效率成( )
比例。
反
5.修一条路,每天修的米数和需要的天数成
( )比例。
6. 已知x和y的关系是正比例关系,根据表中条件,
填写下表。
反
2
18
24
24
二、判断题。
1.正比例的图象呈一条直线,反比例的图象
呈一条曲线。 ( )
2.被减数一定,减数和差成反比例。 ( )
3.每天做题的数量一定,做题的总数量和天
数成正比例。 ( )
4. 生产效率一定,生产的总量和生产的时间
成反比例。 ( )
√
×
×
√
三、选择题。
1.飞机的速度一定,飞行的时间与路程( )。
A. 成正比例 B. 成反比例 C. 不成比例
2.下列说法中,正确的是( )。
A. 图上距离和实际距离成反比例
A
C
B. 三角形的面积一定,底和对应的高成正比例
C. 正方体的棱长总和与它的棱长成正比例
四、判断下面各题中的两个量是否成比例?如果
成比例,成什么比例,并说明理由。
1、长方体的体积一定,它的底面积和高。
成反比例,因为底面积和高的乘积即长方体的体积一定。
2、除数一定,被除数和商。
成正比例,因为被除数和商的比值也就是除数一定。
