人教版2020年春数学九年级下册:26.1.2 反比例函数的图象和性质(二)达标检测(含答案)
文档属性
| 名称 | 人教版2020年春数学九年级下册:26.1.2 反比例函数的图象和性质(二)达标检测(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 144.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-22 00:00:00 | ||
图片预览



文档简介
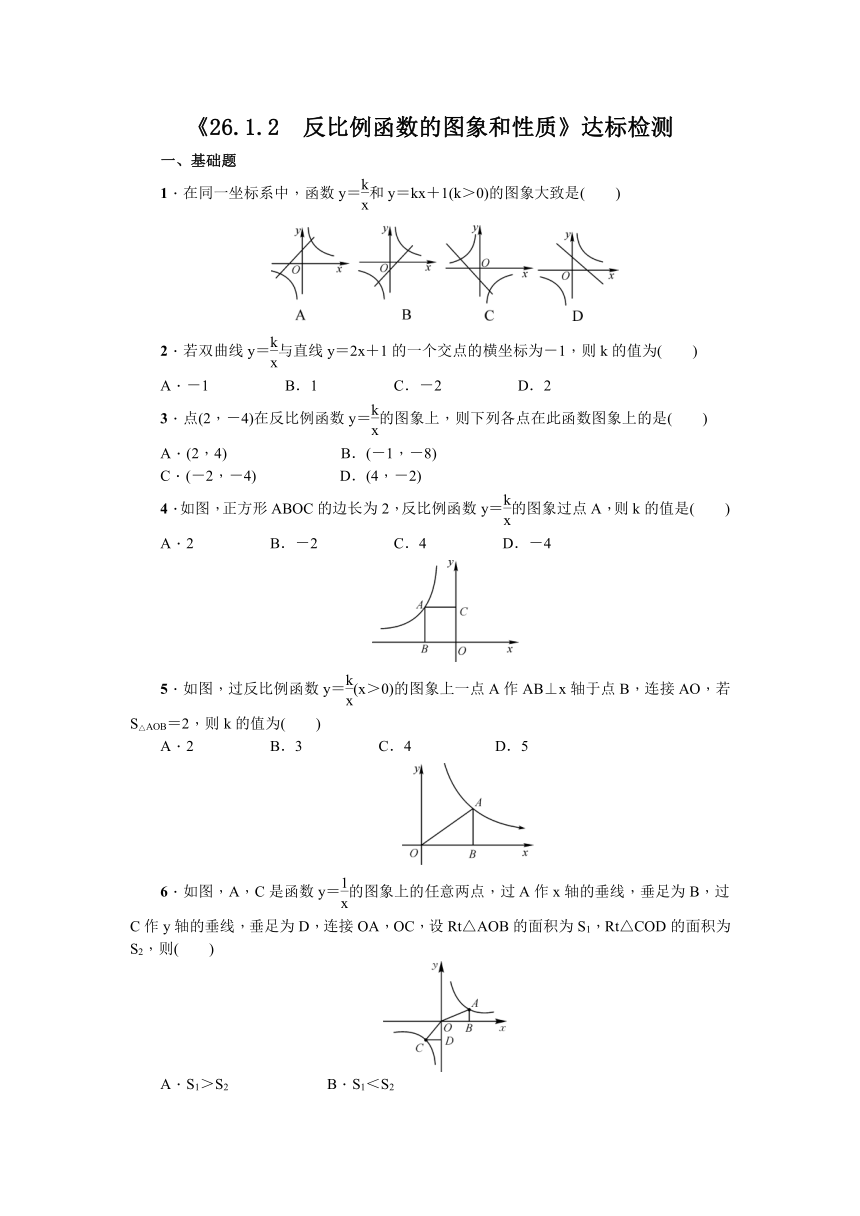
《26.1.2 反比例函数的图象和性质》达标检测
一、基础题
1.在同一坐标系中,函数y=和y=kx+1(k>0)的图象大致是( )
2.若双曲线y=与直线y=2x+1的一个交点的横坐标为-1,则k的值为( )
A.-1 B.1 C.-2 D.2
3.点(2,-4)在反比例函数y=的图象上,则下列各点在此函数图象上的是( )
A.(2,4) B.(-1,-8)
C.(-2,-4) D.(4,-2)
4.如图,正方形ABOC的边长为2,反比例函数y=的图象过点A,则k的值是( )
A.2 B.-2 C.4 D.-4
5.如图,过反比例函数y=(x>0)的图象上一点A作AB⊥x轴于点B,连接AO,若S△AOB=2,则k的值为( )
A.2 B.3 C.4 D.5
6.如图,A,C是函数y=的图象上的任意两点,过A作x轴的垂线,垂足为B,过C作y轴的垂线,垂足为D,连接OA,OC,设Rt△AOB的面积为S1,Rt△COD的面积为S2,则( )
A.S1>S2 B.S1<S2
C.S1=S2 D.S1和S2的大小关系不能确定
7.图象经过点A(-2,-4)的反比例函数的解析式为 .
8.如图,一次函数y1=kx+b(k≠0)和反比例函数y2=(m≠0)的图象交于点A(-1,6),B(a,-2).
(1)求一次函数与反比例函数的解析式;
(2)根据图象直接写出y1>y2时,x的取值范围.
二、提升题
9.定义新运算:a?b=则函数y=3?x的图象大致是( )
10.正方形ABCD的顶点A(2,2),B(-2,2),C(-2,-2),反比例函数y=与y=-的图象均与正方形ABCD的边相交,如图,则图中的阴影部分的面积是( )
A.2 B.4 C.8 D.6
11.一次函数y=kx+b(k≠0)的图象经过A(-1,-4),B(2,2)两点,P为反比例函数y=图象上的一个动点,O为坐标原点,过P作y轴的垂线,垂足为C,则△PCO的面积为( )
A.2 B.4 C.8 D.不确定
12.双曲线y1、y2在第一象限的图象如图,y1=,过y1上的任意一点A,作x轴的平行线交y2于B,交y轴于C,若S△AOB=1,则y2的解析式是 .
13.如图,直线y=x+2与双曲线y=相交于点A(m,3),与x轴交于点C.
(1)求双曲线解析式;[来源:Z§xx§k.Com]
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.
14.已知反比例函数y=的图象的一支位于第一象限.
(1)判断该函数图象的另一支所在的象限,并求m的取值范围;
(2)如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,若△OAB的面积为6,求m的值.
15.如图,已知A(-4,),B(-1,2)是一次函数y=ax+b与反比例函数y=(m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求P点坐标.
参考答案
一、基础题
1.A 2.B 3.D 4.D 5.C 6.C 7.y=
8.解:(1)把点A(-1,6)代入反比例函数y2=(m≠0),得m=-1×6=-6,∴y2=-.
将B(a,-2)代入y2=-,得-2=,解得a=3,
∴B(3,-2).
将A(-1,6),B(3,-2)代入一次函数y1=kx+b,得
∴
∴y1=-2x+4.
(2)x<-1或0二、提升题
9.B 10.C 11.A 12.y2=
13.解:(1)把A(m,3)代入直线解析式,得3=m+2,解得m=2,∴A(2,3).
把A(2,3)代入y=,得k=6,∴双曲线解析式为y=.
(2)对于直线y=x+2,令y=0,得到x=-4,
∴C(-4,0).
设P(x,0),可得PC=|x+4|,∵△ACP面积为3,
∴|x+4|·3=3,即|x+4|=2.
解得x=-2或x=-6.
∴点P坐标为(-2,0)或(-6,0).
14.解:(1)∵该函数图象的一支位于第一象限,
∴该函数图象的另一支位于第三象限.
∴m-7>0,即m>7.
∴m的取值范围是m>7.
(2)设点A的坐标为(x,y).
∵点B与点A关于x轴对称,
∴B点坐标为(x,-y).
∴AB的距离为2y.
∵S△OAB=6,
∴·2y·x=6.∴xy=6.
∵y=,∴xy=m-7.
∴m-7=6.∴m=13.
15.解:(1)当-4<x<-1时,一次函数大于反比例函数的值.
(2)把A(-4,),B(-1,2)代入y=kx+b,得
解得
∴一次函数解析式为y=x+.
把B(-1,2)代入y=,得m=-1×2=-2.
(3)设P点坐标为(t,t+).
∵△PCA和△PDB面积相等,
∴×·(t+4)=×1·(2-t-),解得t=-.
则t+=.
∴P点坐标为(-,).
一、基础题
1.在同一坐标系中,函数y=和y=kx+1(k>0)的图象大致是( )
2.若双曲线y=与直线y=2x+1的一个交点的横坐标为-1,则k的值为( )
A.-1 B.1 C.-2 D.2
3.点(2,-4)在反比例函数y=的图象上,则下列各点在此函数图象上的是( )
A.(2,4) B.(-1,-8)
C.(-2,-4) D.(4,-2)
4.如图,正方形ABOC的边长为2,反比例函数y=的图象过点A,则k的值是( )
A.2 B.-2 C.4 D.-4
5.如图,过反比例函数y=(x>0)的图象上一点A作AB⊥x轴于点B,连接AO,若S△AOB=2,则k的值为( )
A.2 B.3 C.4 D.5
6.如图,A,C是函数y=的图象上的任意两点,过A作x轴的垂线,垂足为B,过C作y轴的垂线,垂足为D,连接OA,OC,设Rt△AOB的面积为S1,Rt△COD的面积为S2,则( )
A.S1>S2 B.S1<S2
C.S1=S2 D.S1和S2的大小关系不能确定
7.图象经过点A(-2,-4)的反比例函数的解析式为 .
8.如图,一次函数y1=kx+b(k≠0)和反比例函数y2=(m≠0)的图象交于点A(-1,6),B(a,-2).
(1)求一次函数与反比例函数的解析式;
(2)根据图象直接写出y1>y2时,x的取值范围.
二、提升题
9.定义新运算:a?b=则函数y=3?x的图象大致是( )
10.正方形ABCD的顶点A(2,2),B(-2,2),C(-2,-2),反比例函数y=与y=-的图象均与正方形ABCD的边相交,如图,则图中的阴影部分的面积是( )
A.2 B.4 C.8 D.6
11.一次函数y=kx+b(k≠0)的图象经过A(-1,-4),B(2,2)两点,P为反比例函数y=图象上的一个动点,O为坐标原点,过P作y轴的垂线,垂足为C,则△PCO的面积为( )
A.2 B.4 C.8 D.不确定
12.双曲线y1、y2在第一象限的图象如图,y1=,过y1上的任意一点A,作x轴的平行线交y2于B,交y轴于C,若S△AOB=1,则y2的解析式是 .
13.如图,直线y=x+2与双曲线y=相交于点A(m,3),与x轴交于点C.
(1)求双曲线解析式;[来源:Z§xx§k.Com]
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.
14.已知反比例函数y=的图象的一支位于第一象限.
(1)判断该函数图象的另一支所在的象限,并求m的取值范围;
(2)如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,若△OAB的面积为6,求m的值.
15.如图,已知A(-4,),B(-1,2)是一次函数y=ax+b与反比例函数y=(m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求P点坐标.
参考答案
一、基础题
1.A 2.B 3.D 4.D 5.C 6.C 7.y=
8.解:(1)把点A(-1,6)代入反比例函数y2=(m≠0),得m=-1×6=-6,∴y2=-.
将B(a,-2)代入y2=-,得-2=,解得a=3,
∴B(3,-2).
将A(-1,6),B(3,-2)代入一次函数y1=kx+b,得
∴
∴y1=-2x+4.
(2)x<-1或0
9.B 10.C 11.A 12.y2=
13.解:(1)把A(m,3)代入直线解析式,得3=m+2,解得m=2,∴A(2,3).
把A(2,3)代入y=,得k=6,∴双曲线解析式为y=.
(2)对于直线y=x+2,令y=0,得到x=-4,
∴C(-4,0).
设P(x,0),可得PC=|x+4|,∵△ACP面积为3,
∴|x+4|·3=3,即|x+4|=2.
解得x=-2或x=-6.
∴点P坐标为(-2,0)或(-6,0).
14.解:(1)∵该函数图象的一支位于第一象限,
∴该函数图象的另一支位于第三象限.
∴m-7>0,即m>7.
∴m的取值范围是m>7.
(2)设点A的坐标为(x,y).
∵点B与点A关于x轴对称,
∴B点坐标为(x,-y).
∴AB的距离为2y.
∵S△OAB=6,
∴·2y·x=6.∴xy=6.
∵y=,∴xy=m-7.
∴m-7=6.∴m=13.
15.解:(1)当-4<x<-1时,一次函数大于反比例函数的值.
(2)把A(-4,),B(-1,2)代入y=kx+b,得
解得
∴一次函数解析式为y=x+.
把B(-1,2)代入y=,得m=-1×2=-2.
(3)设P点坐标为(t,t+).
∵△PCA和△PDB面积相等,
∴×·(t+4)=×1·(2-t-),解得t=-.
则t+=.
∴P点坐标为(-,).
