人教版2020年春数学九年级下册:26.1.2 反比例函数的图象和性质(一)达标检测(含答案)
文档属性
| 名称 | 人教版2020年春数学九年级下册:26.1.2 反比例函数的图象和性质(一)达标检测(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 100.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-22 00:00:00 | ||
图片预览


文档简介
《26.1.2 反比例函数的图象和性质》达标检测
一、选择题
1.对于函数y=-,当x<0时,函数图象位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限[来源:学科网ZXXK]
2.对于函数y=-,下列结论错误的是( )
A.当x>0时,y随x的增大而增大
B.当x<0时,y随x的增大而增大
C.x=1时的函数值大于x=-1时的函数值
D.在函数图象所在的每个象限内,y随x的增大而增大
3.在反比例函数y=图象上有两点A(x1,y1),B(x2,y2),若x1<x2<0,y1<y2,则m的取值范围是( )
A.m> B.m<
C.m≥ D.m≤
4.当x<0时,下列表示函数y=的图象的是( )
5.反比例函数y=的图象经过点(-1,-2),则该反比例函数的图象位于( )
A.第一、二象限 B.第一、三象限
C.第二、四象限 D.第三、四象限
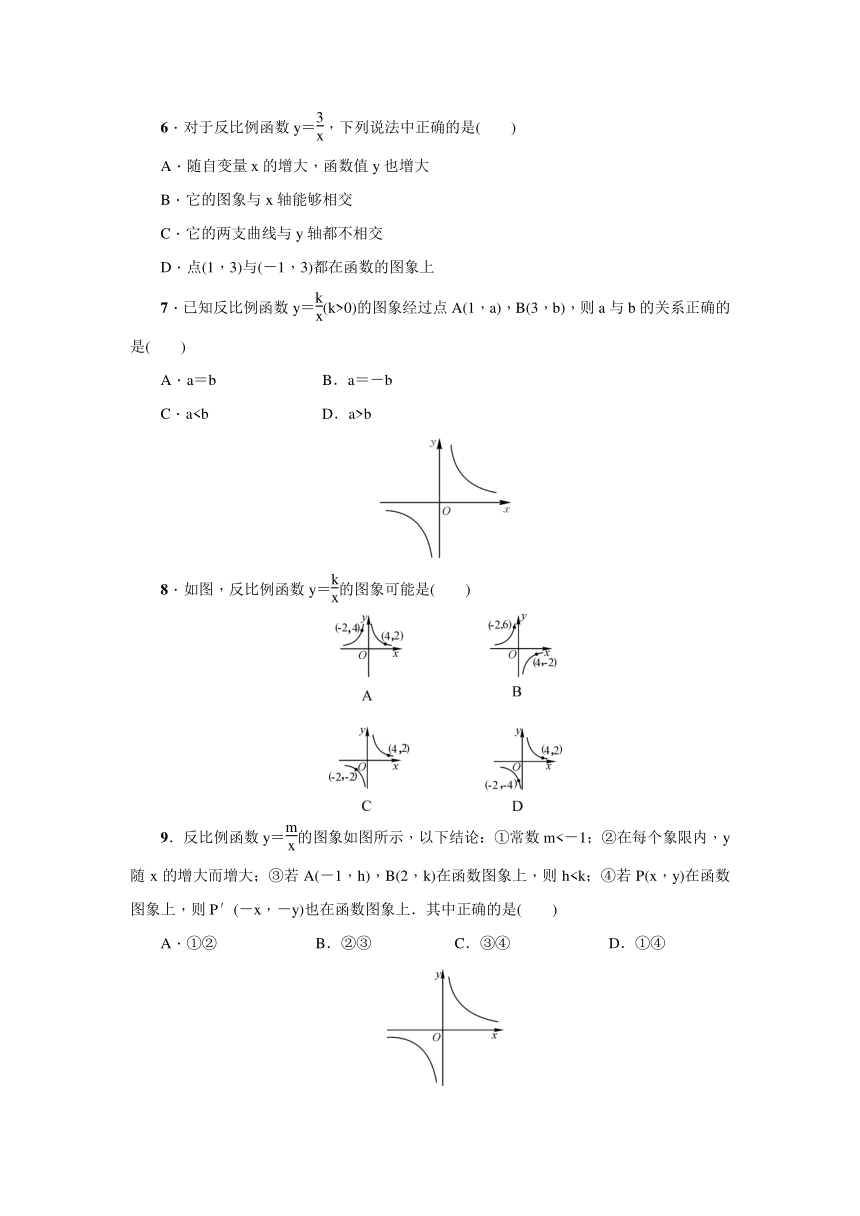
6.对于反比例函数y=,下列说法中正确的是( )
A.随自变量x的增大,函数值y也增大
B.它的图象与x轴能够相交
C.它的两支曲线与y轴都不相交
D.点(1,3)与(-1,3)都在函数的图象上
7.已知反比例函数y=(k>0)的图象经过点A(1,a),B(3,b),则a与b的关系正确的是( )
A.a=b B.a=-b
C.ab
8.如图,反比例函数y=的图象可能是( )
9.反比例函数y=的图象如图所示,以下结论:①常数m<-1;②在每个象限内,y随x的增大而增大;③若A(-1,h),B(2,k)在函数图象上,则hA.①② B.②③ C.③④ D.①④
二、填空题
10.已知反比例函数y=的图象如图所示,则m的取值范围是 .
11.已知P1(x1,y1),P2(x2,y2)两点都在反比例函数y=的图象上,且x1 y2(填“>”或“<”).
12.已知点(m-1,y1),(m-3,y2)是反比例函数y=(m<0)图象上的两点,则y1
y2.(填“>”“=”或“<”)
13.如图是三个反比例函数图象的分支,则k1,k2,k3的大小关系是 .
14.点(a-1,y1)、(a+1,y2)在反比例函数y=(k>0)的图象上,若y1<y2,则a的取值范围是 .
三、综合题
15.如图,已知反比例函数y=(k≠0)的图象经过点A(-2,8).
(1)求这个反比例函数的解析式;
(2)若(2,y1),(4,y2)是这个反比例函数图象上的两个点,请比较y1,y2的大小,并说明理由.
16.已知反比例函数y=(k≠0)的图象经过点(1,-k+2).
(1)求这个反比例函数的解析式;
(2)若(a,y1),(a+1,y2)是这个反比例函数图象上的两个点,请比较y1,y2的大小,并说明理由.
17.已知反比例函数y=(m为常数)的图象在第一、三象限.
(1)求m的取值范围;
(2)如图,若该反比例函数的图象经过?ABOD的顶点D,点A,B的坐标分别为(0,3),(-2,0),求出该反比例函数的解析式;
(3)若E(x1,y1),F(x2,y2)都在该反比例函数的图象上,且x1>x2>0,那么y1和y2有怎样的大小关系?
参考答案
一、选择题
1.B 2.C 3.A 4.D 5.B
6.C 7.D 8.D 9.C
二、填空题
10.m<1 11.> 12.>
13.k1<k3<k2 14.-1<a<1
三、综合题
15.解:(1)y=-.
(2)y1<y2.理由:
∵k=-16<0,
∴在每一个象限内,函数值y随x的增大而增大.
又∵点(2,y1),(4,y2)都在第四象限,且2<4,
∴y1<y2.
16.解:(1)∵反比例函数y=(k≠0)的图象经过点(1,-k+2),
∴-k+2=,解得k=1.
∴这个反比例函数的解析式是y=.
(2)①当a>0时,则a<a+1,[来源:学科网ZXXK]
∵反比例函数y=的图象在第一象限内,y随x的增大而减小,
∴y1>y2.
②当-1<a<0时,则a+1>0,由图象知y1③当a<-1时,则a<a+1,
∵反比例函数y=的图象在第三象限内,y随x的增大而减小,
∴y1>y2.
综上所述,当a>0或a<-1时,y1>y2;
当-117.解:(1)根据题意,得1-2m>0,解得m<.
(2)∵四边形ABOD为平行四边形,
∴AD∥OB,AD=OB=2.
∴D点坐标为(2,3).
∴1-2m=2×3=6.
∴该反比例函数的解析式为y=.
(3)∵x1>x2>0,
∴E,F两点都在第一象限.
又∵在每一个象限内,函数值y随x的增大而减小,
∴y1<y2.
一、选择题
1.对于函数y=-,当x<0时,函数图象位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限[来源:学科网ZXXK]
2.对于函数y=-,下列结论错误的是( )
A.当x>0时,y随x的增大而增大
B.当x<0时,y随x的增大而增大
C.x=1时的函数值大于x=-1时的函数值
D.在函数图象所在的每个象限内,y随x的增大而增大
3.在反比例函数y=图象上有两点A(x1,y1),B(x2,y2),若x1<x2<0,y1<y2,则m的取值范围是( )
A.m> B.m<
C.m≥ D.m≤
4.当x<0时,下列表示函数y=的图象的是( )
5.反比例函数y=的图象经过点(-1,-2),则该反比例函数的图象位于( )
A.第一、二象限 B.第一、三象限
C.第二、四象限 D.第三、四象限
6.对于反比例函数y=,下列说法中正确的是( )
A.随自变量x的增大,函数值y也增大
B.它的图象与x轴能够相交
C.它的两支曲线与y轴都不相交
D.点(1,3)与(-1,3)都在函数的图象上
7.已知反比例函数y=(k>0)的图象经过点A(1,a),B(3,b),则a与b的关系正确的是( )
A.a=b B.a=-b
C.ab
8.如图,反比例函数y=的图象可能是( )
9.反比例函数y=的图象如图所示,以下结论:①常数m<-1;②在每个象限内,y随x的增大而增大;③若A(-1,h),B(2,k)在函数图象上,则h
二、填空题
10.已知反比例函数y=的图象如图所示,则m的取值范围是 .
11.已知P1(x1,y1),P2(x2,y2)两点都在反比例函数y=的图象上,且x1
12.已知点(m-1,y1),(m-3,y2)是反比例函数y=(m<0)图象上的两点,则y1
y2.(填“>”“=”或“<”)
13.如图是三个反比例函数图象的分支,则k1,k2,k3的大小关系是 .
14.点(a-1,y1)、(a+1,y2)在反比例函数y=(k>0)的图象上,若y1<y2,则a的取值范围是 .
三、综合题
15.如图,已知反比例函数y=(k≠0)的图象经过点A(-2,8).
(1)求这个反比例函数的解析式;
(2)若(2,y1),(4,y2)是这个反比例函数图象上的两个点,请比较y1,y2的大小,并说明理由.
16.已知反比例函数y=(k≠0)的图象经过点(1,-k+2).
(1)求这个反比例函数的解析式;
(2)若(a,y1),(a+1,y2)是这个反比例函数图象上的两个点,请比较y1,y2的大小,并说明理由.
17.已知反比例函数y=(m为常数)的图象在第一、三象限.
(1)求m的取值范围;
(2)如图,若该反比例函数的图象经过?ABOD的顶点D,点A,B的坐标分别为(0,3),(-2,0),求出该反比例函数的解析式;
(3)若E(x1,y1),F(x2,y2)都在该反比例函数的图象上,且x1>x2>0,那么y1和y2有怎样的大小关系?
参考答案
一、选择题
1.B 2.C 3.A 4.D 5.B
6.C 7.D 8.D 9.C
二、填空题
10.m<1 11.> 12.>
13.k1<k3<k2 14.-1<a<1
三、综合题
15.解:(1)y=-.
(2)y1<y2.理由:
∵k=-16<0,
∴在每一个象限内,函数值y随x的增大而增大.
又∵点(2,y1),(4,y2)都在第四象限,且2<4,
∴y1<y2.
16.解:(1)∵反比例函数y=(k≠0)的图象经过点(1,-k+2),
∴-k+2=,解得k=1.
∴这个反比例函数的解析式是y=.
(2)①当a>0时,则a<a+1,[来源:学科网ZXXK]
∵反比例函数y=的图象在第一象限内,y随x的增大而减小,
∴y1>y2.
②当-1<a<0时,则a+1>0,由图象知y1
∵反比例函数y=的图象在第三象限内,y随x的增大而减小,
∴y1>y2.
综上所述,当a>0或a<-1时,y1>y2;
当-1
(2)∵四边形ABOD为平行四边形,
∴AD∥OB,AD=OB=2.
∴D点坐标为(2,3).
∴1-2m=2×3=6.
∴该反比例函数的解析式为y=.
(3)∵x1>x2>0,
∴E,F两点都在第一象限.
又∵在每一个象限内,函数值y随x的增大而减小,
∴y1<y2.
