人教版数学四年级下册 5.3 三角形的内角和 课件(共29张PPT)
文档属性
| 名称 | 人教版数学四年级下册 5.3 三角形的内角和 课件(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-22 20:57:38 | ||
图片预览







文档简介
(共29张PPT)
人教版小学数学四年级下册 第五单元
三角形的内角和
动
物
王
国
你认为哪一个三角形的
内角和度数最大?为什么?
我家的房顶侧面最大,是一个锐角三角形,所以我家的三角形内角和最大。
我家的房顶侧面是一个直角三角形,有一个直角,所以我家的三角形的内角和度数最大。
你们俩说的都不对,我家的房顶的侧面是一个钝角三角形,有一个钝角,所以我家的三角形的内角和度数才最大。
自主探究:
1、什么是三角形的内角?
2、三角形有几个内角?
3、什么是三角形的内角和?
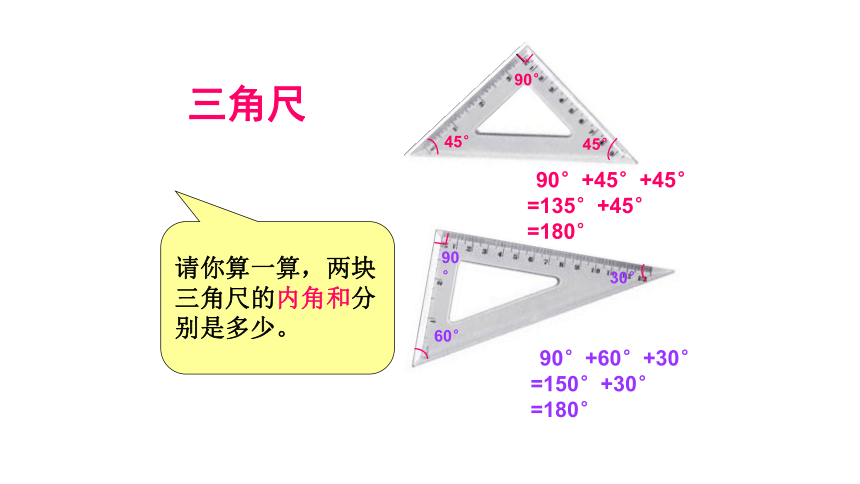
三角尺
请你算一算,两块
三角尺的内角和分
别是多少。
90°
45°
45°
90°
60°
30°
90°+45°+45°
=135°+45°
=180°
90°+60°+30°
=150°+30°
=180°
猜一猜 想一想
大小、形状不同的三角形,
它们的内角和都一样吗?都是
180°吗?
小组活动:
请你们四人小组通过互相
讨论交流办法验证三角形的内
角和。
活动要求:
(1)请你选择一个三角形,用量角
器测量出这个三角形的每个内
角的度数,并标出每个内角的
度数。(取整数)
(2)最后计算出三个角的和是多少。
活动一:
量一量
你还有其他方法证明三角形
的内角和是180°吗?
撕一撕、折一折,看看能不能
把三角形的三个内角拼成什么?
活动二:
撕一 撕
拼一 拼
合作要求:
四人小组分工合作,把三角形的三个角撕
下来,把它们拼在一起,看看能拼成什么。
3
2
3
1
平角:1800
拼一拼
活动三:
折一折
1
1
2
2
3
1
2
1
2
3
3
1
2
3
1
2
3
钝角三角形
锐角三角形
直角三角形
折一折
结论:
三角形的内角
和是180°。
此时,你想对它们说点什么呢?
我家的房顶最大,侧面是一个锐角三角形,所以我家的三角形内角和最大。
我家的房顶侧面是一个直角三角形,有一个直角,所以我家的三角形的内角和度数最大。
你们俩说的都不对,我家的房顶侧面是一个钝角三角形,有一个钝角,所以我家的三角形的内角和度数才最大。
帕斯卡( 1623~1662 ),法国数学家、物理学家,近代概率论的奠基者。早在300多年前这位法国著名的科学家就已经发现了“任何三角形的内角和都是180°”,而他当时只有12岁。
帕斯卡是怎么证明的呢?我们一起来看看:
长方形的四个角是直角
内角和=4×90°=360°
沿对角线分为两个
相同的直角三角形
直角三角形的内角和
360°÷2=180°
(180°+ 180°)-(90°+ 90°)
=360°- 180°
= 180°
180°
180°
锐角三角形
其中有两个直角拼在一起成了一条直线
(180°+ 180°)-(90°+ 90°)
=360°- 180°
= 180°
180°
180°
钝角三角形
谁能帮帕斯卡验证
钝角三角形的内角和?
在能组成三角形的三个角后面画“√”
50°
50°
50°
40°
50°
19°
32°
100°
30°
30°
120°
90°
( )
( )
( )
( )
√
√
(1)
(2)
(3)
(4)
三角形∠1=140°,∠3=25°,求∠2的度数。
140°
25°
?
做一做
1、下面三角形的内角和是多少度?
比一比
①
②
“超级变变变”
2、把下面的三角形平均分成两个三角形,每个三
角形的内角和是多少度?
180°
180°
“超级变变变”
3、说出每个三角形的内角和,把这两个三角形拼
成一个大三角形,所得的大三角形的内角和是多少度?
想一想、说一说
1、一个直角三角形中最多有( )个直角,为什么?
2、一个钝角三角形中最多有( )个钝角,为什么?
这节课你有什么收获?
过关检测题
选做题:△ABC中,已知∠A=40 ° ,∠B-∠C=30° ,
请分别求∠A、∠B、∠C的度数。
1、在一个直角三角形中,已知其中一个锐角是40°,
求另一个锐角是多少度。
2、 △ABC中,已知∠A=35°,∠C=70°。求∠B。
作业:
把学习的欢乐带回家!请你今天
回家与爸爸、妈妈分享你的收获。
谢谢指导!
人教版小学数学四年级下册 第五单元
三角形的内角和
动
物
王
国
你认为哪一个三角形的
内角和度数最大?为什么?
我家的房顶侧面最大,是一个锐角三角形,所以我家的三角形内角和最大。
我家的房顶侧面是一个直角三角形,有一个直角,所以我家的三角形的内角和度数最大。
你们俩说的都不对,我家的房顶的侧面是一个钝角三角形,有一个钝角,所以我家的三角形的内角和度数才最大。
自主探究:
1、什么是三角形的内角?
2、三角形有几个内角?
3、什么是三角形的内角和?
三角尺
请你算一算,两块
三角尺的内角和分
别是多少。
90°
45°
45°
90°
60°
30°
90°+45°+45°
=135°+45°
=180°
90°+60°+30°
=150°+30°
=180°
猜一猜 想一想
大小、形状不同的三角形,
它们的内角和都一样吗?都是
180°吗?
小组活动:
请你们四人小组通过互相
讨论交流办法验证三角形的内
角和。
活动要求:
(1)请你选择一个三角形,用量角
器测量出这个三角形的每个内
角的度数,并标出每个内角的
度数。(取整数)
(2)最后计算出三个角的和是多少。
活动一:
量一量
你还有其他方法证明三角形
的内角和是180°吗?
撕一撕、折一折,看看能不能
把三角形的三个内角拼成什么?
活动二:
撕一 撕
拼一 拼
合作要求:
四人小组分工合作,把三角形的三个角撕
下来,把它们拼在一起,看看能拼成什么。
3
2
3
1
平角:1800
拼一拼
活动三:
折一折
1
1
2
2
3
1
2
1
2
3
3
1
2
3
1
2
3
钝角三角形
锐角三角形
直角三角形
折一折
结论:
三角形的内角
和是180°。
此时,你想对它们说点什么呢?
我家的房顶最大,侧面是一个锐角三角形,所以我家的三角形内角和最大。
我家的房顶侧面是一个直角三角形,有一个直角,所以我家的三角形的内角和度数最大。
你们俩说的都不对,我家的房顶侧面是一个钝角三角形,有一个钝角,所以我家的三角形的内角和度数才最大。
帕斯卡( 1623~1662 ),法国数学家、物理学家,近代概率论的奠基者。早在300多年前这位法国著名的科学家就已经发现了“任何三角形的内角和都是180°”,而他当时只有12岁。
帕斯卡是怎么证明的呢?我们一起来看看:
长方形的四个角是直角
内角和=4×90°=360°
沿对角线分为两个
相同的直角三角形
直角三角形的内角和
360°÷2=180°
(180°+ 180°)-(90°+ 90°)
=360°- 180°
= 180°
180°
180°
锐角三角形
其中有两个直角拼在一起成了一条直线
(180°+ 180°)-(90°+ 90°)
=360°- 180°
= 180°
180°
180°
钝角三角形
谁能帮帕斯卡验证
钝角三角形的内角和?
在能组成三角形的三个角后面画“√”
50°
50°
50°
40°
50°
19°
32°
100°
30°
30°
120°
90°
( )
( )
( )
( )
√
√
(1)
(2)
(3)
(4)
三角形∠1=140°,∠3=25°,求∠2的度数。
140°
25°
?
做一做
1、下面三角形的内角和是多少度?
比一比
①
②
“超级变变变”
2、把下面的三角形平均分成两个三角形,每个三
角形的内角和是多少度?
180°
180°
“超级变变变”
3、说出每个三角形的内角和,把这两个三角形拼
成一个大三角形,所得的大三角形的内角和是多少度?
想一想、说一说
1、一个直角三角形中最多有( )个直角,为什么?
2、一个钝角三角形中最多有( )个钝角,为什么?
这节课你有什么收获?
过关检测题
选做题:△ABC中,已知∠A=40 ° ,∠B-∠C=30° ,
请分别求∠A、∠B、∠C的度数。
1、在一个直角三角形中,已知其中一个锐角是40°,
求另一个锐角是多少度。
2、 △ABC中,已知∠A=35°,∠C=70°。求∠B。
作业:
把学习的欢乐带回家!请你今天
回家与爸爸、妈妈分享你的收获。
谢谢指导!
