3.6 带电粒子在匀强磁场中的运动——有界磁场中的运动 (共19张PPT)
文档属性
| 名称 | 3.6 带电粒子在匀强磁场中的运动——有界磁场中的运动 (共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 681.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-05-22 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
第六节 带电粒子在匀强磁场中的运动
● 知识与技能(1)通过实验知道带电粒子沿着与磁场垂直的方向射入匀强磁场会做圆周运动,圆周运动的半径与磁感应强度的大小和入射的速度的大小有关.(2)通过理论分析知道带电粒子沿着与磁场垂直的方向射入匀强磁场会在磁场中做匀速圆周运动,并能用学过的知识推导出匀速圆周运动的半径公式和周期公式.(3)能够用学过的知识分析、计算有关带电粒子在匀强磁场中受力、运动的问题,了解质谱仪和回旋加速器的工作原理.
教学目标:
(1)通过实验,体会理论和实践相结合的研究方法.(2)通过质谱仪和回旋加速器的学习,提高综合运用力学知识和电学知识的能力.
过程与方法:
重点:带电粒子在匀强磁场中做匀速圆周运动的半径和周期公式,并能用来分析有关问题.
难点:(1)粒子在洛伦兹力作用下做匀速圆周运动.(2)综合运用力学知识、电磁学知识解决带电粒子在复合场中的问题.
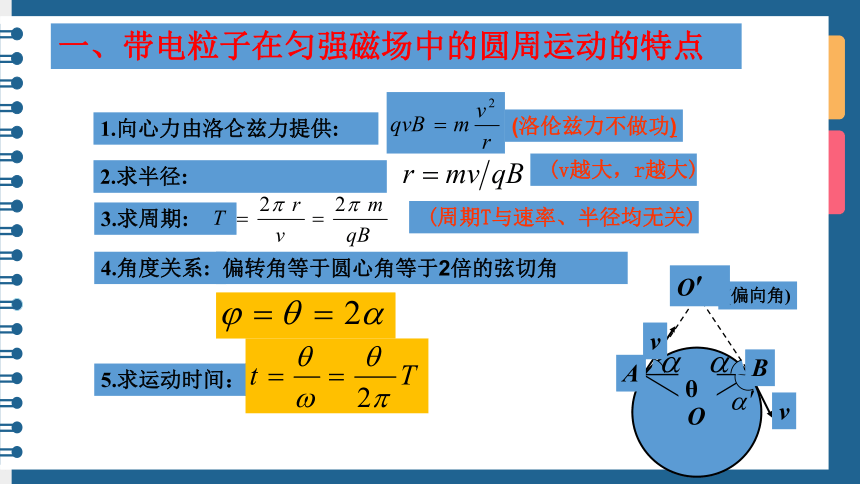
一、带电粒子在匀强磁场中的圆周运动的特点
2.求半径:
1.向心力由洛仑兹力提供:
(v越大,r越大)
3.求周期:
(洛伦兹力不做功)
(周期T与速率、半径均无关)
4.角度关系:
v
θ
v
O
A
B
(偏向角)
O′
偏转角等于圆心角等于2倍的弦切角
5.求运动时间:
介绍洛伦兹力演示仪的工作原理:由电子枪发出的电子射线可以使管内的低压水银蒸气发出辉光,显示出电子的径迹.后进行实验.
【实验】:
在暗室中可以清楚地看到,在没有磁场作用时,电子的径迹是直线;在管外加上匀强磁场(这个磁场是由两个平行的通电环形线圈产生的),电子的径迹变弯曲成圆形.
实验现象:
1.带电粒子沿着磁感线方向飞入匀强磁场,将做什么运动?
2.带电粒子垂直于磁感线方向飞入匀强磁场,又做什么运动呢?
分析:
(1)洛伦兹力方向与速度方向有什么关系?洛伦兹力做功吗?
(2)洛伦兹力对带电粒子的运动起到什么作用?
(3)洛伦兹力的大小改变吗?方向呢?
当带电粒子的初速度方向与磁场方向垂直时,粒子在匀强磁场中做匀速圆周运动.
得出结论:
1.平面运动:分析带电粒子的受力情况,用左手定则明确带电粒子初速度与所受到的洛伦兹力在同一平面内,所以只可能做平面运动.2.做功情况:洛伦兹力不对运动的带电粒子做功,它的速率不变,同时洛伦兹力的大小也不变.3.向心力来源:根据牛顿第二定律,洛伦兹力使运动的带电粒子产生加速度(向心加速度).
进一步分析:
【例题】如图所示,一质量为m,电荷量为q的粒子从容器A下方小孔S1飘入电势差为U的加速电场,然后让粒子垂直进入磁感应强度为B的磁场中,最后打到底片D上.求:
(2)粒子在磁场中运动的轨道半径.
问题:
(1)粒子进入磁场时的速率;
(1)粒子在S1区做初速度为零的匀加速直线运动.由动能定理知,粒子在电场中得到的动能等于电场对它所做的功,即2(1)mv2=qU由此可得v=m(2qU).
解:
解:
(2)粒子做匀速圆周运动所需的向心力由粒子所受的洛伦兹力提供,即qvB=mr(v2).所以粒子的轨道半径为r=qB(mv)=qB2(2mU).
r和进入磁场的速度无关,进入同一磁场时,r∝q(m),而且这些量中,U、B、r可以直接测量,那么,我们可以用装置来测量比荷或算出质量.
[教师讲解]
解决此类问题的一般步骤在解决这类问题时,如何确定圆心、画出粒子的运动轨迹、半径及圆心角,找出几何关系是解题的关键.
小结:
例1.如图,直线MN上方有磁感应强度为B的匀强磁场。正、负电子同时从同一点O,以与MN成30O角的同样速度v射入磁场(电子质量为m,电荷为e),则正负电子在磁场中( )
.
.
300
M
N
B
r
r
O
600
O’
r
r
600
O
A.运动时间相同
B.运动轨迹的半径相同
C.重新回到边界时的速度相同
D.重新回到边界时与O点的距离相等
+e
-e
BCD
感谢您的聆听
THANK YOU
第六节 带电粒子在匀强磁场中的运动
● 知识与技能(1)通过实验知道带电粒子沿着与磁场垂直的方向射入匀强磁场会做圆周运动,圆周运动的半径与磁感应强度的大小和入射的速度的大小有关.(2)通过理论分析知道带电粒子沿着与磁场垂直的方向射入匀强磁场会在磁场中做匀速圆周运动,并能用学过的知识推导出匀速圆周运动的半径公式和周期公式.(3)能够用学过的知识分析、计算有关带电粒子在匀强磁场中受力、运动的问题,了解质谱仪和回旋加速器的工作原理.
教学目标:
(1)通过实验,体会理论和实践相结合的研究方法.(2)通过质谱仪和回旋加速器的学习,提高综合运用力学知识和电学知识的能力.
过程与方法:
重点:带电粒子在匀强磁场中做匀速圆周运动的半径和周期公式,并能用来分析有关问题.
难点:(1)粒子在洛伦兹力作用下做匀速圆周运动.(2)综合运用力学知识、电磁学知识解决带电粒子在复合场中的问题.
一、带电粒子在匀强磁场中的圆周运动的特点
2.求半径:
1.向心力由洛仑兹力提供:
(v越大,r越大)
3.求周期:
(洛伦兹力不做功)
(周期T与速率、半径均无关)
4.角度关系:
v
θ
v
O
A
B
(偏向角)
O′
偏转角等于圆心角等于2倍的弦切角
5.求运动时间:
介绍洛伦兹力演示仪的工作原理:由电子枪发出的电子射线可以使管内的低压水银蒸气发出辉光,显示出电子的径迹.后进行实验.
【实验】:
在暗室中可以清楚地看到,在没有磁场作用时,电子的径迹是直线;在管外加上匀强磁场(这个磁场是由两个平行的通电环形线圈产生的),电子的径迹变弯曲成圆形.
实验现象:
1.带电粒子沿着磁感线方向飞入匀强磁场,将做什么运动?
2.带电粒子垂直于磁感线方向飞入匀强磁场,又做什么运动呢?
分析:
(1)洛伦兹力方向与速度方向有什么关系?洛伦兹力做功吗?
(2)洛伦兹力对带电粒子的运动起到什么作用?
(3)洛伦兹力的大小改变吗?方向呢?
当带电粒子的初速度方向与磁场方向垂直时,粒子在匀强磁场中做匀速圆周运动.
得出结论:
1.平面运动:分析带电粒子的受力情况,用左手定则明确带电粒子初速度与所受到的洛伦兹力在同一平面内,所以只可能做平面运动.2.做功情况:洛伦兹力不对运动的带电粒子做功,它的速率不变,同时洛伦兹力的大小也不变.3.向心力来源:根据牛顿第二定律,洛伦兹力使运动的带电粒子产生加速度(向心加速度).
进一步分析:
【例题】如图所示,一质量为m,电荷量为q的粒子从容器A下方小孔S1飘入电势差为U的加速电场,然后让粒子垂直进入磁感应强度为B的磁场中,最后打到底片D上.求:
(2)粒子在磁场中运动的轨道半径.
问题:
(1)粒子进入磁场时的速率;
(1)粒子在S1区做初速度为零的匀加速直线运动.由动能定理知,粒子在电场中得到的动能等于电场对它所做的功,即2(1)mv2=qU由此可得v=m(2qU).
解:
解:
(2)粒子做匀速圆周运动所需的向心力由粒子所受的洛伦兹力提供,即qvB=mr(v2).所以粒子的轨道半径为r=qB(mv)=qB2(2mU).
r和进入磁场的速度无关,进入同一磁场时,r∝q(m),而且这些量中,U、B、r可以直接测量,那么,我们可以用装置来测量比荷或算出质量.
[教师讲解]
解决此类问题的一般步骤在解决这类问题时,如何确定圆心、画出粒子的运动轨迹、半径及圆心角,找出几何关系是解题的关键.
小结:
例1.如图,直线MN上方有磁感应强度为B的匀强磁场。正、负电子同时从同一点O,以与MN成30O角的同样速度v射入磁场(电子质量为m,电荷为e),则正负电子在磁场中( )
.
.
300
M
N
B
r
r
O
600
O’
r
r
600
O
A.运动时间相同
B.运动轨迹的半径相同
C.重新回到边界时的速度相同
D.重新回到边界时与O点的距离相等
+e
-e
BCD
感谢您的聆听
THANK YOU
