5.2 运动的合成与分解-天津市2020年空中课堂人教版(2019)高中物理必修第二册课件(共26张PPT)
文档属性
| 名称 | 5.2 运动的合成与分解-天津市2020年空中课堂人教版(2019)高中物理必修第二册课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-05-22 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
运动的合成与分解
高一年级 物理
在一次抗洪抢险中,一些群众被泛滥的河流阻隔在水中熄火的汽车上,汽车正对岸上的救援人员试图驾驶冲锋舟,解救被困群众,你认为救援人员应如何驾驶冲锋舟,才能靠近被困汽车呢?
由于,冲锋舟的运动受到引擎驱动与河水的冲击两方面的影响,研究冲锋舟的运动应在一个平面坐标系中进行。我们可以通过分析“蜡块实验”获得启迪,研究冲锋舟救人问题。
一、一个平面运动的实例
在一段封闭的长约1m的玻璃管AB内注满清水,水中放有红蜡做成的小圆柱体R,用胶塞封住玻璃管开口端,把玻璃管倒置,蜡块R沿玻璃管匀速上升。
红蜡块R的运动将如何呢?
如果同时将玻璃管向右匀速移动。
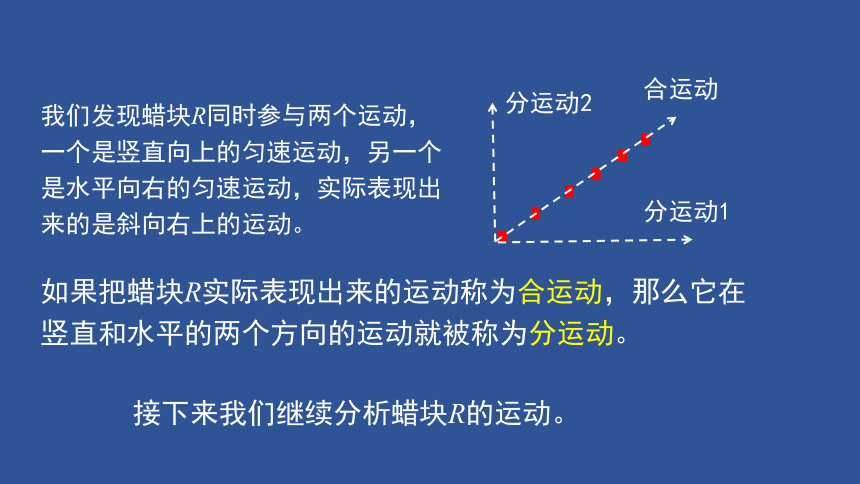
我们发现蜡块R同时参与两个运动,一个是竖直向上的匀速运动,另一个是水平向右的匀速运动,实际表现出来的是斜向右上的运动。
如果把蜡块R实际表现出来的运动称为合运动,那么它在竖直和水平的两个方向的运动就被称为分运动。
接下来我们继续分析蜡块R的运动。
合运动
分运动1
分运动2
首先,我们研究蜡块在竖直平面内做何运动。
1.建立平面直角坐标系
研究蜡块在竖直平面中的运动,需要建立平面直角坐标系。
y
x
o
vy
vx
v
P
x=vxt
y=vyt
蜡块在竖直平面内做直线运动。
2.蜡块的运动轨迹
正比例函数,其图像为过原点的直线。
vy和vx各表示两个匀速运动的速度,它们的比值为常数。
通过刚才的分析,我们发现:通过研究分运动的性质,就可推出合运动的性质。那么在其它方面是否也有这样的规律呢?比如:合运动的速度、位移...等方面。
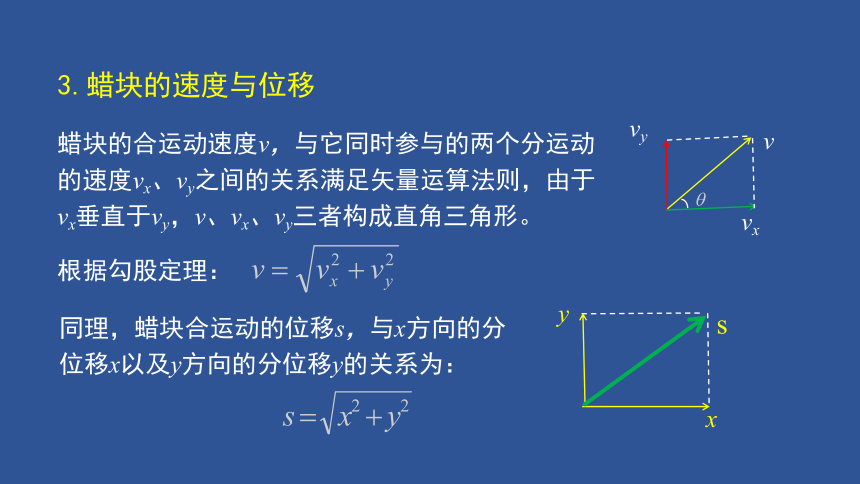
3.蜡块的速度与位移
根据勾股定理:
蜡块的合运动速度v,与它同时参与的两个分运动的速度vx、vy之间的关系满足矢量运算法则,由于vx垂直于vy,v、vx、vy三者构成直角三角形。
vy
vx
v
同理,蜡块合运动的位移s,与x方向的分位移x以及y方向的分位移y的关系为:
x
y
s
vy
vx
v
根据三角函数知识还可以得到vx与vy有下列关系:
通过对“蜡块实验”的分析,我们获得了哪些启迪呢?
(1)物体的合运动的轨迹、位移、速度可由对分运动的研究得出。
(2)物体的合运动与分运动是同时进行的。
(3)两个分运动之间相互独立,互不干扰。
(4)合运动的位移、速度与分运动的位移、速度之间满足矢量运算 法则。
有了上述结论,我们再看冲锋舟救人问题。
被困群众
水流方向
A
B
C
v水
v船
v合
如果把冲锋舟的船头指向被困群众,冲锋舟会到达被困群众处吗?
冲锋舟在水中同时参与了两个分运动:(1)沿船头方向。(2)沿水流方向。
合速度偏向了下游!
救命啊!
船跑哪去了?我们在这儿呢!
被困群众
A
v船
v水
v合
B
v船
v水
v合
v船
v水
v合
冲锋舟怎样行驶才能到达被困群众处呢?
合速度指向B
应使冲锋舟的合速度方向指向被困群众。
冲锋舟船头应偏向上游一个合适角度
v船
v水
v合
冲锋舟的船头应指向...?
完成了救援行动,我们再看今天学习的课题
运动的合成与分解
这是指...?
二、运动的合成与分解
已知分运动求合运动的过程叫做运动的合成,已知合运动求分运动的过程叫做运动的分解。
合运动与分运动的位移、速度、加速度等矢量之间都只遵从矢量运算法则。
思考题
1.前面的“蜡块实验”中如果将玻璃管从静止开始,向右做加速度为a的匀加速直线运动,假设蜡块在竖直方向仍做匀速运动,蜡块的运动轨迹还是一条直线吗?
o
y
x
分析x、y两个方向位移关系:
这是一个二次函数,显然不是直线运动,是一条抛物线
虽然两个分运动都是直线运动,但合运动却是曲线运动
说到这里,你一定有所感悟,说说你的感悟。
既然两个直线运动可以合成为一个曲线运动,那么分析曲线运动时,能不能把它分为两个直线运动呢?
我们解决曲线运动问题的方法,就是将它分解为两个相对简单的直线运动,先研究分运动(位移、速度、加速度),再利用矢量的合成法则,求得合运动的位移、速度、加速度等物理量。需要注意的是:分运动与合运动的时间是相同的。
学习感悟:
课堂练习
【例题】关于合运动与分运动,下列说法正确地是( )
A.合运动的时间等于各个分运动的时间之和
B.合运动的速度一定大于分运动速度
C.当合运动速度增大时,各分运动速度一定增大
D.分运动之间时是彼此独立的互不影响
D
v船
v水
v合
【例题】武装泅渡的战士以一定的速度垂直河岸向对岸游去,当水流匀速时,关于他过河所需时间、发生的位移与水速的关系正确的是:( )
A.水速小时,位移小,时间短;
B.水速大时,位移大,时间短;
C.水速大时,位移大,时间不变;
D .位移、时间与水速无关。
C
水流
d
v水
v人
v合
v合1
v水1
v水增大对v人没有影响,渡河时间:
不变。
【例题】如图为一空间探测器的示意图,p1 、p2、 p3 、p4 是四个喷气发动机,p1、 p3 的连线与空间一固定坐标系的x轴平行,p2、p4的连线与y轴平行,每个发动机开动时,都能向探测器提供推力,但不会使探测器转动,开始时,探测器以恒定的速率v0,向正x方向运动。要使探测器改为正x 偏负y 600的方向以原来的速率v0运动,则 ( )
A.先开动p1 适当时间,再开动p4适当时间
B.先开动p3 适当时间,再开动p2适当时间
C.先开动p3 适当时间,再开动p4适当时间
D.先开动p2 适当时间,再开动p1适当时间
x
y
o
p1
p2
p3
p4
x
y
o
p1
p2
p3
p4
v0
v1
600
改为向正x 偏负y 600的方向运动,速率的大小不变,速度变为v1
选A
解析:
v0
探测器原来沿x正向运动,速度为v0。
vx
vy
应使,
x方向速度:从v0减小为vx,(须开启P1发动机减速)
y方向速度:从0 增大为vy,(须开启P4发动机加速)
【例题】如图所示,汽车以水平方向速度v匀速行驶,到达如图所示位置时,绳子与水平方向的夹角为θ ,此时物体M的速度大小为多少?
v
M
v
M
解析:
M物体的速度,与汽车拉动绳子的速度大小相等。
研究绳子被拉动的速度,应选取绳子与汽车的拴结点A为研究对象。
v
v1
v2
A
A点的合运动方向水平,
一个分运动方向沿绳子方向
另一个分运动方向垂直绳子。
根据数学知识:
课堂小结
(2)物体的合运动与分运动是同时进行的。
(3)分运动之间相互独立,互不影响。
(4)合运动与分运动之间满足矢量运算法则。
(5)分析曲线运动的一般方法是,将它分解为两个直线运动。
(1)合运动、分运动、运动的合成与分解。
课后作业
2.教材P9练习与应用1、2、3、4、5
如果将一个物体以水平初速度抛出,物体将做曲线运动,对于这个曲线运动,我们最好将它分解为哪两个分运动呢?
1.课后思考题
谢谢同学们,再见
运动的合成与分解
高一年级 物理
在一次抗洪抢险中,一些群众被泛滥的河流阻隔在水中熄火的汽车上,汽车正对岸上的救援人员试图驾驶冲锋舟,解救被困群众,你认为救援人员应如何驾驶冲锋舟,才能靠近被困汽车呢?
由于,冲锋舟的运动受到引擎驱动与河水的冲击两方面的影响,研究冲锋舟的运动应在一个平面坐标系中进行。我们可以通过分析“蜡块实验”获得启迪,研究冲锋舟救人问题。
一、一个平面运动的实例
在一段封闭的长约1m的玻璃管AB内注满清水,水中放有红蜡做成的小圆柱体R,用胶塞封住玻璃管开口端,把玻璃管倒置,蜡块R沿玻璃管匀速上升。
红蜡块R的运动将如何呢?
如果同时将玻璃管向右匀速移动。
我们发现蜡块R同时参与两个运动,一个是竖直向上的匀速运动,另一个是水平向右的匀速运动,实际表现出来的是斜向右上的运动。
如果把蜡块R实际表现出来的运动称为合运动,那么它在竖直和水平的两个方向的运动就被称为分运动。
接下来我们继续分析蜡块R的运动。
合运动
分运动1
分运动2
首先,我们研究蜡块在竖直平面内做何运动。
1.建立平面直角坐标系
研究蜡块在竖直平面中的运动,需要建立平面直角坐标系。
y
x
o
vy
vx
v
P
x=vxt
y=vyt
蜡块在竖直平面内做直线运动。
2.蜡块的运动轨迹
正比例函数,其图像为过原点的直线。
vy和vx各表示两个匀速运动的速度,它们的比值为常数。
通过刚才的分析,我们发现:通过研究分运动的性质,就可推出合运动的性质。那么在其它方面是否也有这样的规律呢?比如:合运动的速度、位移...等方面。
3.蜡块的速度与位移
根据勾股定理:
蜡块的合运动速度v,与它同时参与的两个分运动的速度vx、vy之间的关系满足矢量运算法则,由于vx垂直于vy,v、vx、vy三者构成直角三角形。
vy
vx
v
同理,蜡块合运动的位移s,与x方向的分位移x以及y方向的分位移y的关系为:
x
y
s
vy
vx
v
根据三角函数知识还可以得到vx与vy有下列关系:
通过对“蜡块实验”的分析,我们获得了哪些启迪呢?
(1)物体的合运动的轨迹、位移、速度可由对分运动的研究得出。
(2)物体的合运动与分运动是同时进行的。
(3)两个分运动之间相互独立,互不干扰。
(4)合运动的位移、速度与分运动的位移、速度之间满足矢量运算 法则。
有了上述结论,我们再看冲锋舟救人问题。
被困群众
水流方向
A
B
C
v水
v船
v合
如果把冲锋舟的船头指向被困群众,冲锋舟会到达被困群众处吗?
冲锋舟在水中同时参与了两个分运动:(1)沿船头方向。(2)沿水流方向。
合速度偏向了下游!
救命啊!
船跑哪去了?我们在这儿呢!
被困群众
A
v船
v水
v合
B
v船
v水
v合
v船
v水
v合
冲锋舟怎样行驶才能到达被困群众处呢?
合速度指向B
应使冲锋舟的合速度方向指向被困群众。
冲锋舟船头应偏向上游一个合适角度
v船
v水
v合
冲锋舟的船头应指向...?
完成了救援行动,我们再看今天学习的课题
运动的合成与分解
这是指...?
二、运动的合成与分解
已知分运动求合运动的过程叫做运动的合成,已知合运动求分运动的过程叫做运动的分解。
合运动与分运动的位移、速度、加速度等矢量之间都只遵从矢量运算法则。
思考题
1.前面的“蜡块实验”中如果将玻璃管从静止开始,向右做加速度为a的匀加速直线运动,假设蜡块在竖直方向仍做匀速运动,蜡块的运动轨迹还是一条直线吗?
o
y
x
分析x、y两个方向位移关系:
这是一个二次函数,显然不是直线运动,是一条抛物线
虽然两个分运动都是直线运动,但合运动却是曲线运动
说到这里,你一定有所感悟,说说你的感悟。
既然两个直线运动可以合成为一个曲线运动,那么分析曲线运动时,能不能把它分为两个直线运动呢?
我们解决曲线运动问题的方法,就是将它分解为两个相对简单的直线运动,先研究分运动(位移、速度、加速度),再利用矢量的合成法则,求得合运动的位移、速度、加速度等物理量。需要注意的是:分运动与合运动的时间是相同的。
学习感悟:
课堂练习
【例题】关于合运动与分运动,下列说法正确地是( )
A.合运动的时间等于各个分运动的时间之和
B.合运动的速度一定大于分运动速度
C.当合运动速度增大时,各分运动速度一定增大
D.分运动之间时是彼此独立的互不影响
D
v船
v水
v合
【例题】武装泅渡的战士以一定的速度垂直河岸向对岸游去,当水流匀速时,关于他过河所需时间、发生的位移与水速的关系正确的是:( )
A.水速小时,位移小,时间短;
B.水速大时,位移大,时间短;
C.水速大时,位移大,时间不变;
D .位移、时间与水速无关。
C
水流
d
v水
v人
v合
v合1
v水1
v水增大对v人没有影响,渡河时间:
不变。
【例题】如图为一空间探测器的示意图,p1 、p2、 p3 、p4 是四个喷气发动机,p1、 p3 的连线与空间一固定坐标系的x轴平行,p2、p4的连线与y轴平行,每个发动机开动时,都能向探测器提供推力,但不会使探测器转动,开始时,探测器以恒定的速率v0,向正x方向运动。要使探测器改为正x 偏负y 600的方向以原来的速率v0运动,则 ( )
A.先开动p1 适当时间,再开动p4适当时间
B.先开动p3 适当时间,再开动p2适当时间
C.先开动p3 适当时间,再开动p4适当时间
D.先开动p2 适当时间,再开动p1适当时间
x
y
o
p1
p2
p3
p4
x
y
o
p1
p2
p3
p4
v0
v1
600
改为向正x 偏负y 600的方向运动,速率的大小不变,速度变为v1
选A
解析:
v0
探测器原来沿x正向运动,速度为v0。
vx
vy
应使,
x方向速度:从v0减小为vx,(须开启P1发动机减速)
y方向速度:从0 增大为vy,(须开启P4发动机加速)
【例题】如图所示,汽车以水平方向速度v匀速行驶,到达如图所示位置时,绳子与水平方向的夹角为θ ,此时物体M的速度大小为多少?
v
M
v
M
解析:
M物体的速度,与汽车拉动绳子的速度大小相等。
研究绳子被拉动的速度,应选取绳子与汽车的拴结点A为研究对象。
v
v1
v2
A
A点的合运动方向水平,
一个分运动方向沿绳子方向
另一个分运动方向垂直绳子。
根据数学知识:
课堂小结
(2)物体的合运动与分运动是同时进行的。
(3)分运动之间相互独立,互不影响。
(4)合运动与分运动之间满足矢量运算法则。
(5)分析曲线运动的一般方法是,将它分解为两个直线运动。
(1)合运动、分运动、运动的合成与分解。
课后作业
2.教材P9练习与应用1、2、3、4、5
如果将一个物体以水平初速度抛出,物体将做曲线运动,对于这个曲线运动,我们最好将它分解为哪两个分运动呢?
1.课后思考题
谢谢同学们,再见
