7.1 行星的运动-天津市2020年空中课堂人教版(2019)高中物理必修第二册课件(共25张PPT)
文档属性
| 名称 | 7.1 行星的运动-天津市2020年空中课堂人教版(2019)高中物理必修第二册课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-05-22 21:32:01 | ||
图片预览





文档简介
(共25张PPT)
行星的运动
高一年级 物理
远古学说
天圆地方
地心说
日心说
阿里斯塔克
以太阳为中心
亚里士多德
地球外面有九重天幕
天如鸡子,地如鸡中黄
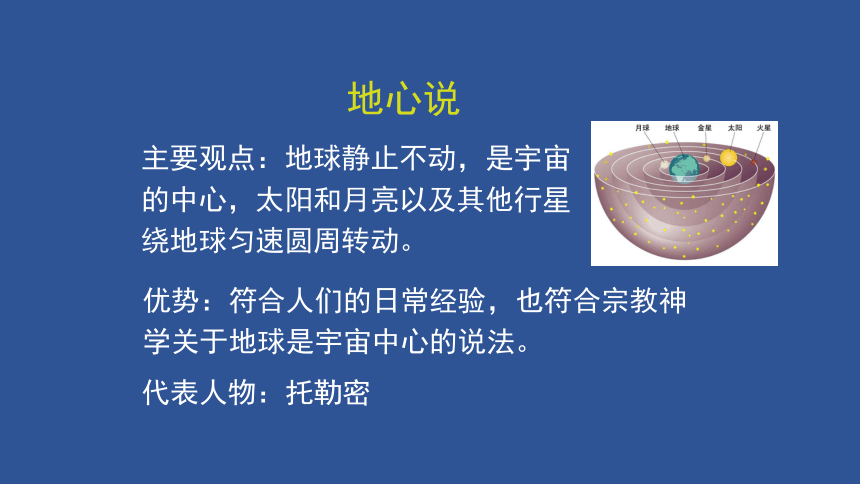
地心说
代表人物:托勒密
优势:符合人们的日常经验,也符合宗教神学关于地球是宇宙中心的说法。
主要观点:地球静止不动,是宇宙的中心,太阳和月亮以及其他行星绕地球匀速圆周转动。
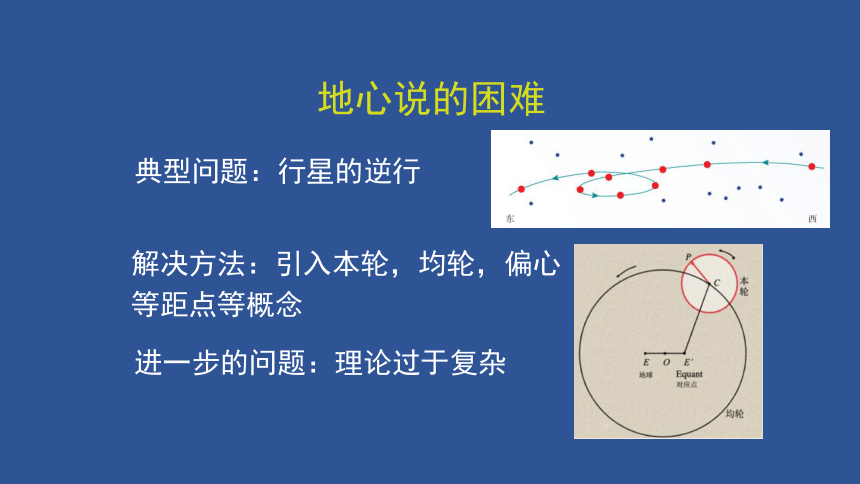
地心说的困难
典型问题:行星的逆行
解决方法:引入本轮,均轮,偏心等距点等概念
进一步的问题:理论过于复杂
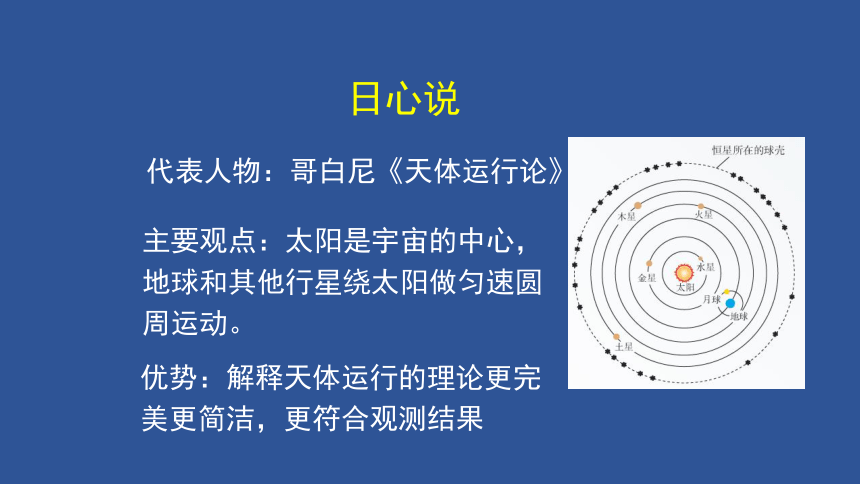
日心说
代表人物:哥白尼《天体运行论》
主要观点:太阳是宇宙的中心,地球和其他行星绕太阳做匀速圆周运动。
优势:解释天体运行的理论更完美更简洁,更符合观测结果
第谷:肉眼观星最精确的人
改进测量仪器和测量手段,减小测量误差
坚持用地心说解释观测数据
第 谷(丹麦)
把天体位置测量的误差由10′减少到2′
德国天文学家开普勒的探索
花费十几年时间整理第谷的数据
开普勒(德国)
在这期间,伽利略发明了望远镜
以日心说为基础,试图用数学方法得出行星运动的一般规律
开普勒面临的第一个问题
根据圆周运动轨道计算出的结果与第谷的观测数据有8′的偏差
结论:行星绕太阳做圆周运动的模型是错误的
问题:圆周运动轨道和第谷的观测数据哪个才是准确的?
火星为什么那么不听话?
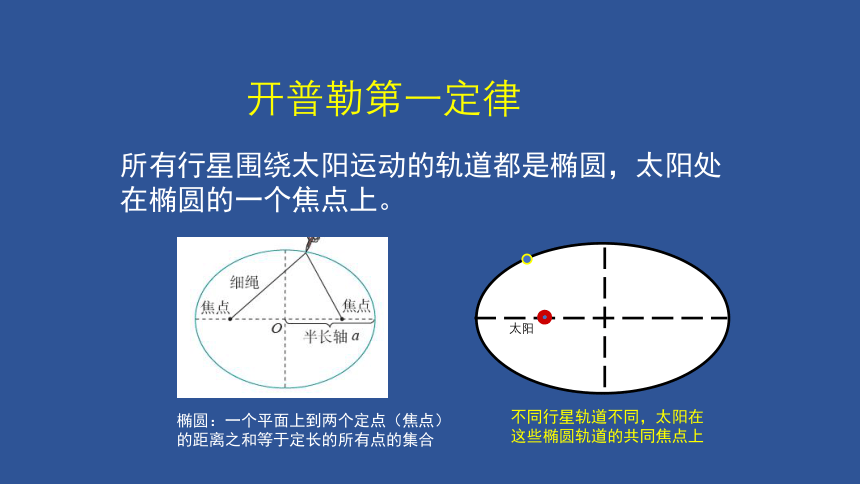
开普勒第一定律
所有行星围绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上。
太阳
椭圆:一个平面上到两个定点(焦点)的距离之和等于定长的所有点的集合
不同行星轨道不同,太阳在这些椭圆轨道的共同焦点上
开普勒的新问题
理论:行星沿椭圆轨迹运动时速率是定值
结论:行星沿椭圆轨道运动的速率是不断变化的
问题:以等速模型计算的结果与观测数据不符
为什么又是火星!!
开普勒第二定律
对于每一个行星而言,太阳和行星的连线在相等的时间内扫过相等的面积。
当行星离太阳比较近时,运动速度比较大,而离太阳比较远时速度比较小;在近日点速度最大,远日点速度最小
开普勒的最终目标
有没有一个能把所有行星联系在一起的简单法则呢?
行星 半长轴a(AU) 公转周期(Y,年)
水星 0.387 0.241
金星 0.723 0.615
地球 1.00 1.00
火星 1.52 1.88
木星 5.20 11.9
土星 9.54 29.5
注:1AU=1.5×1011m,即地球轨道的半长轴
1.00
1.00
1.00
1.00
1.01
1.01
开普勒第三定律
所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等。
以地球和土星为例:
高中阶段对行星运动的近似化处理
行星绕太阳运动的轨道十分接近圆,太阳处在圆心。
行星绕太阳做匀速圆周运动
行星轨道半径的三次方跟它的公转周期的二次方的比值都相等
开普勒三定律适用于所有绕中心天体运行的星系,但不同星系的 k 值不同
以地球绕太阳运动为例
以月球绕地球运动为例
课堂小结
天圆地方
地心说
远古
公元二世纪
托勒密
地心说
1543
哥白尼
日心说
1546
第谷
出生
1600
开普勒
任第谷助手
1609
开普勒
第一定律
第二定律
1619
开普勒
第三定律
牛顿
万有引力定律
练习:某行星绕太阳运行的椭圆轨道如图所示,F1和F2是椭圆轨道的两个焦点,行星在M点的速率比在N点的大,则太阳是位于( )
A.F1 B.M点
C.F2 D.N点
F1
F2
M
N
A
练习:某行星沿椭圆轨道运行,近日点离太阳距离为a,远日点离太阳距离为b,过近日点时行星的速率为va,则过远日点时速率为( )
A、 B、 C、 D、
解:扇形面积公式为弧长与半径乘积的一半,根据开普勒第二定律有:
C
练习:某一人造卫星绕地球做匀速圆周运动,其轨道半径约为月球绕地球轨道半径的四分之一,则此卫星运行的周期大约是( )
A.l~4天之间
B.4~8天之间
C.8~16天之间
D.16~20天之间
解析:月球绕地球的公转周期约为28天,根据开普勒第三定律得
代入数据可得卫星周期约为3.5天
A
练习:有两颗行星,它们绕太阳的运动可认为是匀速圆周运动,且公转周期之比为8∶1,则
(1)它们的轨道半径之比为 ( )
A . 4∶1 B . 8∶1
C . 2∶1 D . 1∶4
(2)两行星的公转速度之比为 ( )
A . 2∶1 B . 4∶1
C . 1∶2 D . 1∶4
解析:(1)根据题目条件:T1: T2=8:1,由开普勒第三定律有 ,可得: r1: r2=4:1。
有两颗行星,它们绕太阳的运动可认为是匀速圆周运动,且公转周期之比为8∶1,则
(1)它们的轨道半径的比为 ( )
A . 4∶1 B . 8∶1
C . 2∶1 D . 1∶4
A
(2)两行星的公转速度之比为 ( )
A . 2∶1 B . 4∶1
C . 1∶2 D . 1∶4
C
解析:(2)行星绕太阳做匀速圆周运动,因此: ,可得:
练习:飞船沿半径为R的圆周绕地球运动,其周期为T,地球半径为R0,若飞船要返回地面,可在轨道上某点A处将速率 降到适当的数值,从而使飞船沿着以地心为焦点的椭圆轨道运行,椭圆与地球表面在B点相切,求飞船由A点到B点所需要的时间?
解:飞船绕椭圆轨道运行的半长轴为
根据开普勒第三定律得
飞船由A点到B点的时间
课后作业
1、自己动手试着按照前面讲的方法画一个椭圆。
3、在课本上查找探究类实验,看看你的办法用到了吗?
2、要探究两个物理量之间的关系,一般采取的办法有哪些?查阅资料,试着总结一下。
结束语
人们在认识和开拓世界的过程中,依靠自身对世界的理解不断发展天文学说,然后又反哺人类对于世界的进一步认识和开拓。开普勒三定律的发现,是偶然也是历史发展的必然,从此以后,行星的复杂运动便失去了神秘性,并为数十年后牛顿发现万有引力定律铺平了道路。
行星的运动
高一年级 物理
远古学说
天圆地方
地心说
日心说
阿里斯塔克
以太阳为中心
亚里士多德
地球外面有九重天幕
天如鸡子,地如鸡中黄
地心说
代表人物:托勒密
优势:符合人们的日常经验,也符合宗教神学关于地球是宇宙中心的说法。
主要观点:地球静止不动,是宇宙的中心,太阳和月亮以及其他行星绕地球匀速圆周转动。
地心说的困难
典型问题:行星的逆行
解决方法:引入本轮,均轮,偏心等距点等概念
进一步的问题:理论过于复杂
日心说
代表人物:哥白尼《天体运行论》
主要观点:太阳是宇宙的中心,地球和其他行星绕太阳做匀速圆周运动。
优势:解释天体运行的理论更完美更简洁,更符合观测结果
第谷:肉眼观星最精确的人
改进测量仪器和测量手段,减小测量误差
坚持用地心说解释观测数据
第 谷(丹麦)
把天体位置测量的误差由10′减少到2′
德国天文学家开普勒的探索
花费十几年时间整理第谷的数据
开普勒(德国)
在这期间,伽利略发明了望远镜
以日心说为基础,试图用数学方法得出行星运动的一般规律
开普勒面临的第一个问题
根据圆周运动轨道计算出的结果与第谷的观测数据有8′的偏差
结论:行星绕太阳做圆周运动的模型是错误的
问题:圆周运动轨道和第谷的观测数据哪个才是准确的?
火星为什么那么不听话?
开普勒第一定律
所有行星围绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上。
太阳
椭圆:一个平面上到两个定点(焦点)的距离之和等于定长的所有点的集合
不同行星轨道不同,太阳在这些椭圆轨道的共同焦点上
开普勒的新问题
理论:行星沿椭圆轨迹运动时速率是定值
结论:行星沿椭圆轨道运动的速率是不断变化的
问题:以等速模型计算的结果与观测数据不符
为什么又是火星!!
开普勒第二定律
对于每一个行星而言,太阳和行星的连线在相等的时间内扫过相等的面积。
当行星离太阳比较近时,运动速度比较大,而离太阳比较远时速度比较小;在近日点速度最大,远日点速度最小
开普勒的最终目标
有没有一个能把所有行星联系在一起的简单法则呢?
行星 半长轴a(AU) 公转周期(Y,年)
水星 0.387 0.241
金星 0.723 0.615
地球 1.00 1.00
火星 1.52 1.88
木星 5.20 11.9
土星 9.54 29.5
注:1AU=1.5×1011m,即地球轨道的半长轴
1.00
1.00
1.00
1.00
1.01
1.01
开普勒第三定律
所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等。
以地球和土星为例:
高中阶段对行星运动的近似化处理
行星绕太阳运动的轨道十分接近圆,太阳处在圆心。
行星绕太阳做匀速圆周运动
行星轨道半径的三次方跟它的公转周期的二次方的比值都相等
开普勒三定律适用于所有绕中心天体运行的星系,但不同星系的 k 值不同
以地球绕太阳运动为例
以月球绕地球运动为例
课堂小结
天圆地方
地心说
远古
公元二世纪
托勒密
地心说
1543
哥白尼
日心说
1546
第谷
出生
1600
开普勒
任第谷助手
1609
开普勒
第一定律
第二定律
1619
开普勒
第三定律
牛顿
万有引力定律
练习:某行星绕太阳运行的椭圆轨道如图所示,F1和F2是椭圆轨道的两个焦点,行星在M点的速率比在N点的大,则太阳是位于( )
A.F1 B.M点
C.F2 D.N点
F1
F2
M
N
A
练习:某行星沿椭圆轨道运行,近日点离太阳距离为a,远日点离太阳距离为b,过近日点时行星的速率为va,则过远日点时速率为( )
A、 B、 C、 D、
解:扇形面积公式为弧长与半径乘积的一半,根据开普勒第二定律有:
C
练习:某一人造卫星绕地球做匀速圆周运动,其轨道半径约为月球绕地球轨道半径的四分之一,则此卫星运行的周期大约是( )
A.l~4天之间
B.4~8天之间
C.8~16天之间
D.16~20天之间
解析:月球绕地球的公转周期约为28天,根据开普勒第三定律得
代入数据可得卫星周期约为3.5天
A
练习:有两颗行星,它们绕太阳的运动可认为是匀速圆周运动,且公转周期之比为8∶1,则
(1)它们的轨道半径之比为 ( )
A . 4∶1 B . 8∶1
C . 2∶1 D . 1∶4
(2)两行星的公转速度之比为 ( )
A . 2∶1 B . 4∶1
C . 1∶2 D . 1∶4
解析:(1)根据题目条件:T1: T2=8:1,由开普勒第三定律有 ,可得: r1: r2=4:1。
有两颗行星,它们绕太阳的运动可认为是匀速圆周运动,且公转周期之比为8∶1,则
(1)它们的轨道半径的比为 ( )
A . 4∶1 B . 8∶1
C . 2∶1 D . 1∶4
A
(2)两行星的公转速度之比为 ( )
A . 2∶1 B . 4∶1
C . 1∶2 D . 1∶4
C
解析:(2)行星绕太阳做匀速圆周运动,因此: ,可得:
练习:飞船沿半径为R的圆周绕地球运动,其周期为T,地球半径为R0,若飞船要返回地面,可在轨道上某点A处将速率 降到适当的数值,从而使飞船沿着以地心为焦点的椭圆轨道运行,椭圆与地球表面在B点相切,求飞船由A点到B点所需要的时间?
解:飞船绕椭圆轨道运行的半长轴为
根据开普勒第三定律得
飞船由A点到B点的时间
课后作业
1、自己动手试着按照前面讲的方法画一个椭圆。
3、在课本上查找探究类实验,看看你的办法用到了吗?
2、要探究两个物理量之间的关系,一般采取的办法有哪些?查阅资料,试着总结一下。
结束语
人们在认识和开拓世界的过程中,依靠自身对世界的理解不断发展天文学说,然后又反哺人类对于世界的进一步认识和开拓。开普勒三定律的发现,是偶然也是历史发展的必然,从此以后,行星的复杂运动便失去了神秘性,并为数十年后牛顿发现万有引力定律铺平了道路。
