吉林省伊通满族自治县第九中学校七年级数学上册1.2.4 绝对值课件(共18张PPT)
文档属性
| 名称 | 吉林省伊通满族自治县第九中学校七年级数学上册1.2.4 绝对值课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 919.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-24 08:47:27 | ||
图片预览





文档简介
(共18张PPT)
a
-a
相反数
复 习:
什么是数轴?
数轴是规定了原点、正方向、单位长度的直线
什么是相反数?
只有符号不同的两个数叫做互为相反数。
规定:0的相反数是0。
数轴的三要素
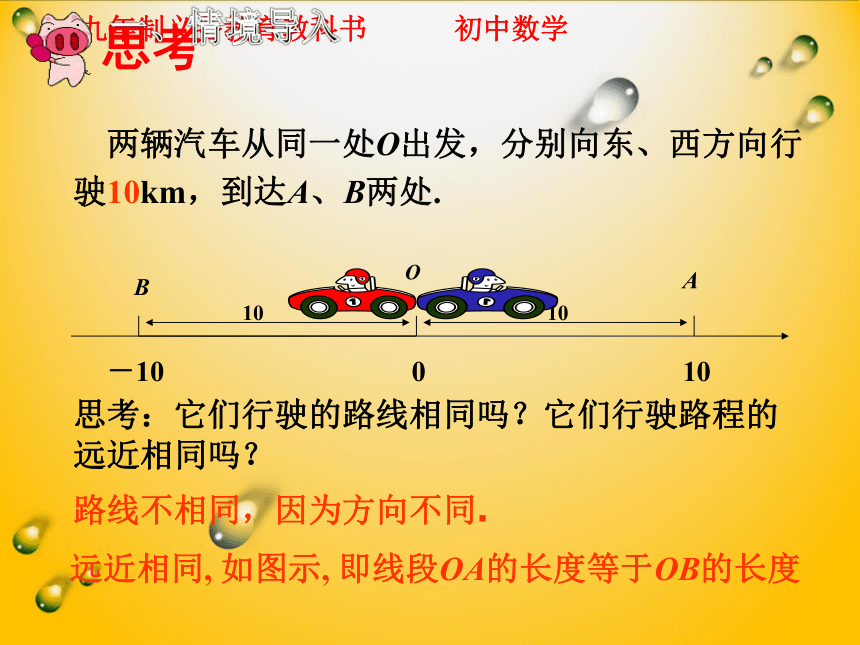
两辆汽车从同一处O出发,分别向东、西方向行驶10km,到达A、B两处.
思考:它们行驶的路线相同吗?它们行驶路程的远近相同吗?
路线不相同,因为方向不同.
远近相同, 如图示, 即线段OA的长度等于OB的长度
O
B
A
0
10
-10
10
10
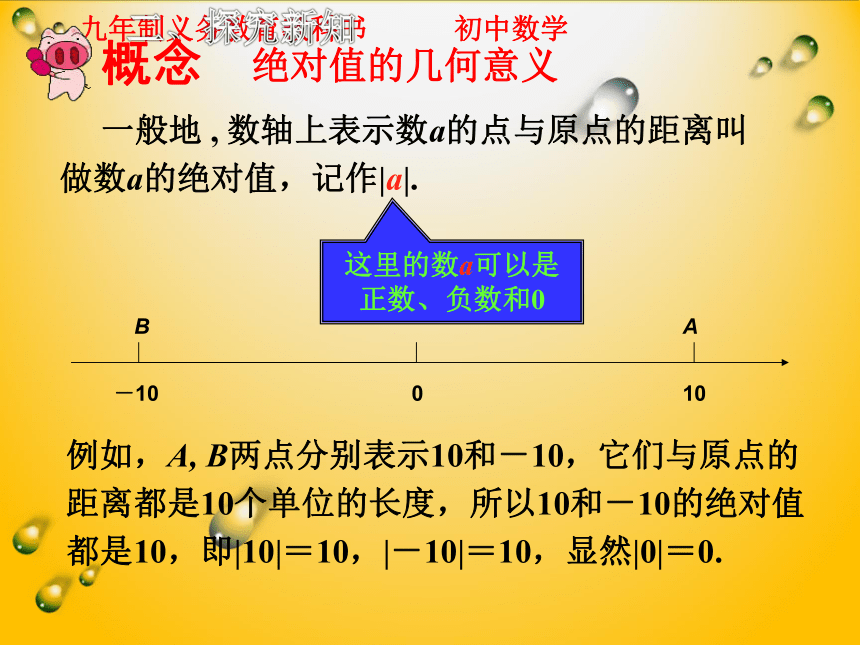
一般地 , 数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|.
例如,A, B两点分别表示10和-10,它们与原点的距离都是10个单位的长度,所以10和-10的绝对值都是10,即|10|=10,|-10|=10,显然|0|=0.
这里的数a可以是正数、负数和0
A
B
绝对值的几何意义
巩固练习
根据绝对值的定义,求下列各数的
绝对值.
填空:
(1)|3|=______;(2)|1.5|=______;
(3)|-3|=______;(4)|-1.5|=______;
(5)|0|=_____.
解决这些问题后,你能得到什么结论?
探索下列问题
3
1.5
3
1.5
0
由绝对值的定义可知:一个正数的绝对值是___________;一个负数的绝对值是它的__________________;0的绝对值是_______.
(1)当a是正数时,|a|=____________
(2)当a是负数时,|a|=____________
(3)当a是0时,|a|=____________
它本身
相反数
0
a
-a
0
绝对值的代数意义
你可以给 a 取些具体数值检验你填写的结果是否正确.
1. 写出下列各数的绝对值:
|6|=6
|-8|=8
|-3.9|=3.9
|100|=100
|0|=0
解:
2. 判断下列说法是否正确
(1)符号相反的数互为相反数; ( )
(4)当a≠0时,∣a∣总是大于0. ( )
(2)一个数的绝对值越大,表示它的点在数轴上越靠右 ; ( )
(3)一个数的绝对值越大,表示它的点在数轴上离原点越远; ( )
×
√
×
√
3. 判断下列各式是否正确:
(1)∣5∣= ∣-5∣;
(2)- ∣5∣= ∣-5∣;
(3)-5= ∣-5∣.
√
×
×
求下列各组相反数的绝对值。
(2)|0.6|=0.6 |-0.6|=0.8
例1.
互为相反数的两个数的绝对值有什么关系?
原点
-3到原点的距离是3
+3到原点的距离是3
互为相反数的两个数的绝对值相等.
(1)绝对值是3的数有几个? 各是什么?
(2)绝对值是0的数有几个?它是什么?
(3)是否存在绝对值是-2的数?若存在,请说出来?
想一想:
本节课里你学到了什么?
绝对值的概念;
如何求一个数的绝对值;
一个数的绝对值总是大于或等于0的.
课本第14页 第5题
2的绝对值等于( )
A.2 B. ????? C. —2 D. — ?????
2. —2011的绝对值为( )
A. 2011 B. ???? C. —2011 D. — ?????????????
3. — ?????的绝对值为( )
A.2 B. ????? C. —2 D. — ?????
4. 如果a与1互为相反数,则︱a︱等于( )
A.2 B. —2 C. 1 D. —1
5. —︱—3︱=( )
A.3 B. —3 C. ????? D. — ?????
6. 计算:(1) 3 —︱— ???︱;(2)︱—7.3︱×︱3.5︱; (3) ︱— ?????︱÷︱— ?????︱
7. 下列说法错误的是( )
一个正数的绝对值一定是正数
B. 一个负数的绝对值一定是正数
C. 任何数的绝对值都是正数
D. 任何数的绝对值都不是负数
8. 如果a与—1互为相反数,则︱a+2011︱=________。
9. 用“>”“<”“=”填空: —3____—6,— ____—, —5____—8,—︱—3.2︱_____(+3.2), 0_____—(— ?????)
10. 写出一个比—1小的实数_____
11. 用“<”把下列各数连接起来:—2,4,— ????????,0,1.5, ????????。
12. 绝对值大于1而小于5的所有整数是_________。
13. 数a的相反数比a大,则下列说法正确的是( )
A. 数a一定是正数 B. 数a一定是负数
C. 数a一定不是负数 D. 数a一定是0
14. 下列说法中,正确的是( )
A. 0是最小的整数 B. 1是最小的自然数
C. 0是最小的自然数 D. —1是最小的负整数
15. a是绝对值最小的数,b是相反数等于它本身的数,求2010a—2011b的值。
a
-a
相反数
复 习:
什么是数轴?
数轴是规定了原点、正方向、单位长度的直线
什么是相反数?
只有符号不同的两个数叫做互为相反数。
规定:0的相反数是0。
数轴的三要素
两辆汽车从同一处O出发,分别向东、西方向行驶10km,到达A、B两处.
思考:它们行驶的路线相同吗?它们行驶路程的远近相同吗?
路线不相同,因为方向不同.
远近相同, 如图示, 即线段OA的长度等于OB的长度
O
B
A
0
10
-10
10
10
一般地 , 数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|.
例如,A, B两点分别表示10和-10,它们与原点的距离都是10个单位的长度,所以10和-10的绝对值都是10,即|10|=10,|-10|=10,显然|0|=0.
这里的数a可以是正数、负数和0
A
B
绝对值的几何意义
巩固练习
根据绝对值的定义,求下列各数的
绝对值.
填空:
(1)|3|=______;(2)|1.5|=______;
(3)|-3|=______;(4)|-1.5|=______;
(5)|0|=_____.
解决这些问题后,你能得到什么结论?
探索下列问题
3
1.5
3
1.5
0
由绝对值的定义可知:一个正数的绝对值是___________;一个负数的绝对值是它的__________________;0的绝对值是_______.
(1)当a是正数时,|a|=____________
(2)当a是负数时,|a|=____________
(3)当a是0时,|a|=____________
它本身
相反数
0
a
-a
0
绝对值的代数意义
你可以给 a 取些具体数值检验你填写的结果是否正确.
1. 写出下列各数的绝对值:
|6|=6
|-8|=8
|-3.9|=3.9
|100|=100
|0|=0
解:
2. 判断下列说法是否正确
(1)符号相反的数互为相反数; ( )
(4)当a≠0时,∣a∣总是大于0. ( )
(2)一个数的绝对值越大,表示它的点在数轴上越靠右 ; ( )
(3)一个数的绝对值越大,表示它的点在数轴上离原点越远; ( )
×
√
×
√
3. 判断下列各式是否正确:
(1)∣5∣= ∣-5∣;
(2)- ∣5∣= ∣-5∣;
(3)-5= ∣-5∣.
√
×
×
求下列各组相反数的绝对值。
(2)|0.6|=0.6 |-0.6|=0.8
例1.
互为相反数的两个数的绝对值有什么关系?
原点
-3到原点的距离是3
+3到原点的距离是3
互为相反数的两个数的绝对值相等.
(1)绝对值是3的数有几个? 各是什么?
(2)绝对值是0的数有几个?它是什么?
(3)是否存在绝对值是-2的数?若存在,请说出来?
想一想:
本节课里你学到了什么?
绝对值的概念;
如何求一个数的绝对值;
一个数的绝对值总是大于或等于0的.
课本第14页 第5题
2的绝对值等于( )
A.2 B. ????? C. —2 D. — ?????
2. —2011的绝对值为( )
A. 2011 B. ???? C. —2011 D. — ?????????????
3. — ?????的绝对值为( )
A.2 B. ????? C. —2 D. — ?????
4. 如果a与1互为相反数,则︱a︱等于( )
A.2 B. —2 C. 1 D. —1
5. —︱—3︱=( )
A.3 B. —3 C. ????? D. — ?????
6. 计算:(1) 3 —︱— ???︱;(2)︱—7.3︱×︱3.5︱; (3) ︱— ?????︱÷︱— ?????︱
7. 下列说法错误的是( )
一个正数的绝对值一定是正数
B. 一个负数的绝对值一定是正数
C. 任何数的绝对值都是正数
D. 任何数的绝对值都不是负数
8. 如果a与—1互为相反数,则︱a+2011︱=________。
9. 用“>”“<”“=”填空: —3____—6,— ____—, —5____—8,—︱—3.2︱_____(+3.2), 0_____—(— ?????)
10. 写出一个比—1小的实数_____
11. 用“<”把下列各数连接起来:—2,4,— ????????,0,1.5, ????????。
12. 绝对值大于1而小于5的所有整数是_________。
13. 数a的相反数比a大,则下列说法正确的是( )
A. 数a一定是正数 B. 数a一定是负数
C. 数a一定不是负数 D. 数a一定是0
14. 下列说法中,正确的是( )
A. 0是最小的整数 B. 1是最小的自然数
C. 0是最小的自然数 D. —1是最小的负整数
15. a是绝对值最小的数,b是相反数等于它本身的数,求2010a—2011b的值。
