人教版(2019版)高一物理必修第二册第八章 8.2重力势能 24张PPT
文档属性
| 名称 | 人教版(2019版)高一物理必修第二册第八章 8.2重力势能 24张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 983.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-05-23 07:13:09 | ||
图片预览






文档简介
(共24张PPT)
人教版 必修第二册
第八章 机械能守恒定律
8.2 重力势能
功是能量变化的量度
课时一:重力做功和重力势能的关系
课时二:弹力做功和弹性势能的关系
重力势能
课时一:重力做功和重力势能的关系
(1)比较球A,C可得出影响重力势能大小的因素是_____________。
(2)比较球A,B可得出影响重力势能大小的因素是_____________。
知识回顾:如图所示,在“探究影响重力势能大小的因素”实验中,有三个实心的、大小相同的铁球A,铁球B和塑料球C,球A,C离沙地高度相同。现让三个球同时从图示位置由静止释放,球落到沙地上的状态如图中虚线球所示。
影响重力势能的两个因素:
物体质量(重力)越大,重力势能越大;
物体高度越高,重力势能越大。
一、重力做功
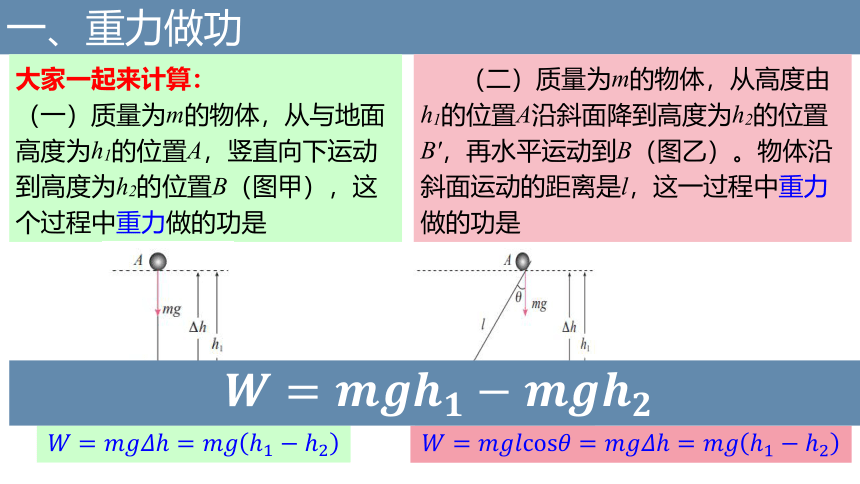
大家一起来计算:
(一)质量为m的物体,从与地面高度为h1的位置A,竖直向下运动到高度为h2的位置B(图甲),这个过程中重力做的功是
(二)质量为m的物体,从高度由h1的位置A沿斜面降到高度为h2的位置B′,再水平运动到B(图乙)。物体沿斜面运动的距离是l,这一过程中重力做的功是
一、重力做功
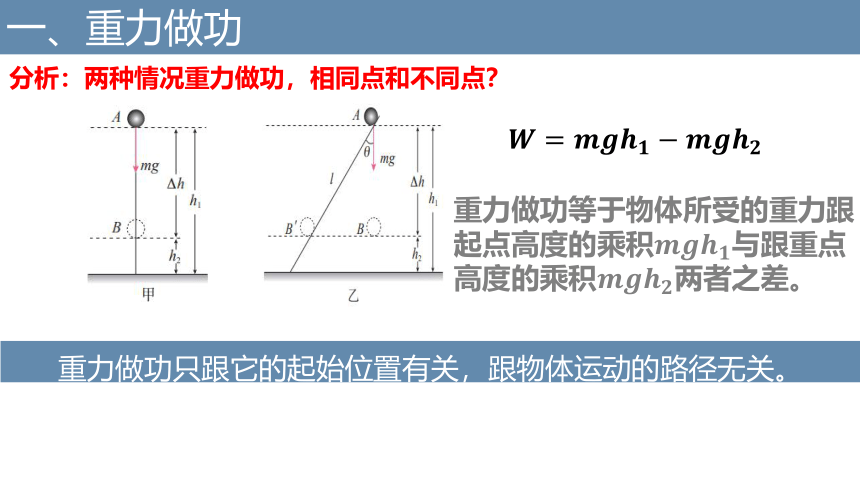
分析:两种情况重力做功,相同点和不同点?
重力做功等于物体所受的重力跟起点高度的乘积与跟重点高度的乘积两者之差。
A
B
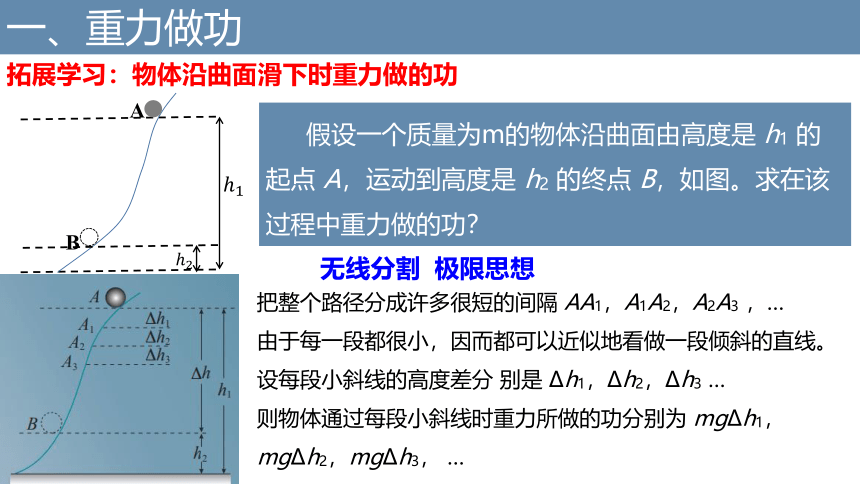
拓展学习:物体沿曲面滑下时重力做的功
假设一个质量为m的物体沿曲面由高度是 h1 的起点 A,运动到高度是 h2 的终点 B,如图。求在该过程中重力做的功?
一、重力做功
无线分割 极限思想
把整个路径分成许多很短的间隔 AA1,A1A2,A2A3 ,…
由于每一段都很小,因而都可以近似地看做一段倾斜的直线。设每段小斜线的高度差分 别是 ?h1,?h2,?h3 …
则物体通过每段小斜线时重力所做的功分别为 mg?h1,mg?h2,mg?h3, …
拓展学习:物体沿曲面滑下时重力做的功
假设一个质量为m的物体沿曲面由高度是 h1 的起点 A,运动到高度是 h2 的终点 B,如图。求在该过程中重力做的功?
一、重力做功
无线分割 极限思想
物体通过整个路径时重力所做的功,等于重力在每小段上所做的功的代数和,即
WG=mg?h1+mg?h2+mg?h3+…
=mg(?h1+?h2+?h3+ …)
=mgΔh
=mgh1-mgh2
二、重力势能
与物体质量m和物体高度h有关;
质量越大、高度越高,mgh越大。
1.表达式: 重力势能:
2.是一种能量,标量,单位:J焦耳
3.不同重力势能可用下脚标区分。
三、重力势能与重力做功的关系
初位置的重力势能
末位置的重力势能
1. 当物体由高处向低处运动时:重力做正功,即WG>0,EP1>EP2,重力势能减小;
2. 当物体由低处向高处运动时:重力做负功,即WG<0,EP1<EP2,重力势能增大
重力做功对应着重力势能的变化
三、重力势能与重力做功的关系
若重力做的功与路径有关,即对应于同样的起点和终点,重力对同一物体所做的功,随物体运动路径的不同而不同,我们还能把mgh叫作物体的重力势能吗?为什么?
四、重力势能的相对性
重力势能:
高度h总是相对于某一水平面来说的,实际上是把水平面的高度取做0。
物体的重力势能也总是相对于某一水平面的,这个水平面叫做参考平面。
在参考平面上,物体的重力势能取为0。
选择哪个水平面做参考平面,可视研究问题的方便而定。
通常选择地面为参考平面。
四、重力势能的相对性
提示:
选择不同的参考平面,物体重力势能的数值是不同的。
对选定的参考平面而言,上方物体的高度是正值,重力 势能也是正值;下方物体的高度是负值,重力势能也是负值。 负值的重力势能,表示物体在这个位置具有的重力势能比在 参考平面上具有的重力势能要小。
例:以二楼的地面作为参考平面,二楼房间里 A 处的物体具有正 的重力势能,一楼房间里 B 处的物体具有负的重力势能。
1.重力做功:
重力做功与重力大小和起始点有关,与路径无关。
2. 重力势能:
3.重力势能与重力做功的关系:
4.重力势能的相对性
课时小结
带有思考、
带有研究、
带有挑战的
物理学习。
课时二:弹力做功和弹性势能的关系
本课时以学生自主探究为主
本课时主要任务:
1.探究如何求弹力做功;
2.探究弹性势能表达式。
知识回顾:
1.功的表达式?适用条件?
2.重力做功的表达式?
3.弹力的表达式?
4.弹性势能的影响因素?
发生弹性形变的物体的各部分之间,由于有弹力的相互作用,也具有势能,这种势能叫做弹性势能。
问题与思考
一、弹力做功
弹力表达式:(胡克定律,l---形变量)
弹力为变力,变力做功如何求解?可以用吗?
复习上周变力做功的专题,参考匀变速直线运动求位移的方式求解
请同学们尝试自己推导弹力做功的表达式。
提示:把弹簧拉伸时,弹力与位移方向相反。缓慢拉动弹簧时,弹力与拉力等大反向,可先求拉力做功!
匀速直线运动v-t图象
v
t
O
位移x=vt
类比
一、弹力做功
匀变速直线运动v-t图象(面积为位移)
恒力F-l图象
F
l
O
恒力做功W=Fl
O
F拉
l
拉力(变力)F-l 图象
弹力做功表达式是?
l
F拉
0
l
Δl1
Δl2
Δl3
Δl5
Δl4
F2
F3
F4
F5
F1
拉力所做的功等于图线与横轴所围的面积
一、弹力做功
k---弹簧劲度系数
l---弹簧形变量
重力做正功:重力势能减少
重力做负功:重力势能增加
重力做的功与重力势能的改变有何关系?
WG= -△EP
思考:弹性势能的大小怎么求?
重力势能
重力做功
二、弹力势能的表达式
类比
类比重力做功和重力势能的关系,思考:弹性势能的大小?
二、弹力势能的表达式
重力势能 弹性势能
重力做功 重力势能变化
重力做正功,重力势能减小;
重力做负功,重力势能增大。
WG= mgh1-mgh2
WG= EP1 - EP2
A点:自然伸长位置,既没压缩也没拉伸。该点弹性势能为0。.
弹簧弹力始终指向恢复形变的方向。
A到B过程,弹力向左,位移向右,弹力做负功,弹性势能增大。
B到A过程,弹力向左,位移向左,弹力做正功,弹性势能减小。
初始弹性势能
末弹性势能:该位置处的弹性势能
弹性势能:
二、弹力势能的表达式
弹性势能和重力势能类比小结
带有思考、
带有研究、
带有挑战的
物理学习。
人教版 必修第二册
第八章 机械能守恒定律
8.2 重力势能
功是能量变化的量度
课时一:重力做功和重力势能的关系
课时二:弹力做功和弹性势能的关系
重力势能
课时一:重力做功和重力势能的关系
(1)比较球A,C可得出影响重力势能大小的因素是_____________。
(2)比较球A,B可得出影响重力势能大小的因素是_____________。
知识回顾:如图所示,在“探究影响重力势能大小的因素”实验中,有三个实心的、大小相同的铁球A,铁球B和塑料球C,球A,C离沙地高度相同。现让三个球同时从图示位置由静止释放,球落到沙地上的状态如图中虚线球所示。
影响重力势能的两个因素:
物体质量(重力)越大,重力势能越大;
物体高度越高,重力势能越大。
一、重力做功
大家一起来计算:
(一)质量为m的物体,从与地面高度为h1的位置A,竖直向下运动到高度为h2的位置B(图甲),这个过程中重力做的功是
(二)质量为m的物体,从高度由h1的位置A沿斜面降到高度为h2的位置B′,再水平运动到B(图乙)。物体沿斜面运动的距离是l,这一过程中重力做的功是
一、重力做功
分析:两种情况重力做功,相同点和不同点?
重力做功等于物体所受的重力跟起点高度的乘积与跟重点高度的乘积两者之差。
A
B
拓展学习:物体沿曲面滑下时重力做的功
假设一个质量为m的物体沿曲面由高度是 h1 的起点 A,运动到高度是 h2 的终点 B,如图。求在该过程中重力做的功?
一、重力做功
无线分割 极限思想
把整个路径分成许多很短的间隔 AA1,A1A2,A2A3 ,…
由于每一段都很小,因而都可以近似地看做一段倾斜的直线。设每段小斜线的高度差分 别是 ?h1,?h2,?h3 …
则物体通过每段小斜线时重力所做的功分别为 mg?h1,mg?h2,mg?h3, …
拓展学习:物体沿曲面滑下时重力做的功
假设一个质量为m的物体沿曲面由高度是 h1 的起点 A,运动到高度是 h2 的终点 B,如图。求在该过程中重力做的功?
一、重力做功
无线分割 极限思想
物体通过整个路径时重力所做的功,等于重力在每小段上所做的功的代数和,即
WG=mg?h1+mg?h2+mg?h3+…
=mg(?h1+?h2+?h3+ …)
=mgΔh
=mgh1-mgh2
二、重力势能
与物体质量m和物体高度h有关;
质量越大、高度越高,mgh越大。
1.表达式: 重力势能:
2.是一种能量,标量,单位:J焦耳
3.不同重力势能可用下脚标区分。
三、重力势能与重力做功的关系
初位置的重力势能
末位置的重力势能
1. 当物体由高处向低处运动时:重力做正功,即WG>0,EP1>EP2,重力势能减小;
2. 当物体由低处向高处运动时:重力做负功,即WG<0,EP1<EP2,重力势能增大
重力做功对应着重力势能的变化
三、重力势能与重力做功的关系
若重力做的功与路径有关,即对应于同样的起点和终点,重力对同一物体所做的功,随物体运动路径的不同而不同,我们还能把mgh叫作物体的重力势能吗?为什么?
四、重力势能的相对性
重力势能:
高度h总是相对于某一水平面来说的,实际上是把水平面的高度取做0。
物体的重力势能也总是相对于某一水平面的,这个水平面叫做参考平面。
在参考平面上,物体的重力势能取为0。
选择哪个水平面做参考平面,可视研究问题的方便而定。
通常选择地面为参考平面。
四、重力势能的相对性
提示:
选择不同的参考平面,物体重力势能的数值是不同的。
对选定的参考平面而言,上方物体的高度是正值,重力 势能也是正值;下方物体的高度是负值,重力势能也是负值。 负值的重力势能,表示物体在这个位置具有的重力势能比在 参考平面上具有的重力势能要小。
例:以二楼的地面作为参考平面,二楼房间里 A 处的物体具有正 的重力势能,一楼房间里 B 处的物体具有负的重力势能。
1.重力做功:
重力做功与重力大小和起始点有关,与路径无关。
2. 重力势能:
3.重力势能与重力做功的关系:
4.重力势能的相对性
课时小结
带有思考、
带有研究、
带有挑战的
物理学习。
课时二:弹力做功和弹性势能的关系
本课时以学生自主探究为主
本课时主要任务:
1.探究如何求弹力做功;
2.探究弹性势能表达式。
知识回顾:
1.功的表达式?适用条件?
2.重力做功的表达式?
3.弹力的表达式?
4.弹性势能的影响因素?
发生弹性形变的物体的各部分之间,由于有弹力的相互作用,也具有势能,这种势能叫做弹性势能。
问题与思考
一、弹力做功
弹力表达式:(胡克定律,l---形变量)
弹力为变力,变力做功如何求解?可以用吗?
复习上周变力做功的专题,参考匀变速直线运动求位移的方式求解
请同学们尝试自己推导弹力做功的表达式。
提示:把弹簧拉伸时,弹力与位移方向相反。缓慢拉动弹簧时,弹力与拉力等大反向,可先求拉力做功!
匀速直线运动v-t图象
v
t
O
位移x=vt
类比
一、弹力做功
匀变速直线运动v-t图象(面积为位移)
恒力F-l图象
F
l
O
恒力做功W=Fl
O
F拉
l
拉力(变力)F-l 图象
弹力做功表达式是?
l
F拉
0
l
Δl1
Δl2
Δl3
Δl5
Δl4
F2
F3
F4
F5
F1
拉力所做的功等于图线与横轴所围的面积
一、弹力做功
k---弹簧劲度系数
l---弹簧形变量
重力做正功:重力势能减少
重力做负功:重力势能增加
重力做的功与重力势能的改变有何关系?
WG= -△EP
思考:弹性势能的大小怎么求?
重力势能
重力做功
二、弹力势能的表达式
类比
类比重力做功和重力势能的关系,思考:弹性势能的大小?
二、弹力势能的表达式
重力势能 弹性势能
重力做功 重力势能变化
重力做正功,重力势能减小;
重力做负功,重力势能增大。
WG= mgh1-mgh2
WG= EP1 - EP2
A点:自然伸长位置,既没压缩也没拉伸。该点弹性势能为0。.
弹簧弹力始终指向恢复形变的方向。
A到B过程,弹力向左,位移向右,弹力做负功,弹性势能增大。
B到A过程,弹力向左,位移向左,弹力做正功,弹性势能减小。
初始弹性势能
末弹性势能:该位置处的弹性势能
弹性势能:
二、弹力势能的表达式
弹性势能和重力势能类比小结
带有思考、
带有研究、
带有挑战的
物理学习。
