10.1.1 对顶角(要点测评+课后集训+答案)
文档属性
| 名称 | 10.1.1 对顶角(要点测评+课后集训+答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-22 22:10:20 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
沪科版数学七年级下册同步课时训练
第10章 相交线、平行线与平移
10.1 相交线
第1课时 对顶角
要点测评 基础达标
要点1 对顶角的概念
1. 下列语句中,关于对顶角的定义的叙述正确的是( )
A. 有公共顶点的两个角
B. 有公共顶点且相等的两个角
C. 一个角的两边分别是另一个角的两边的延长线
D. 一个角的两边分别是另一个角的两边的反向延长线
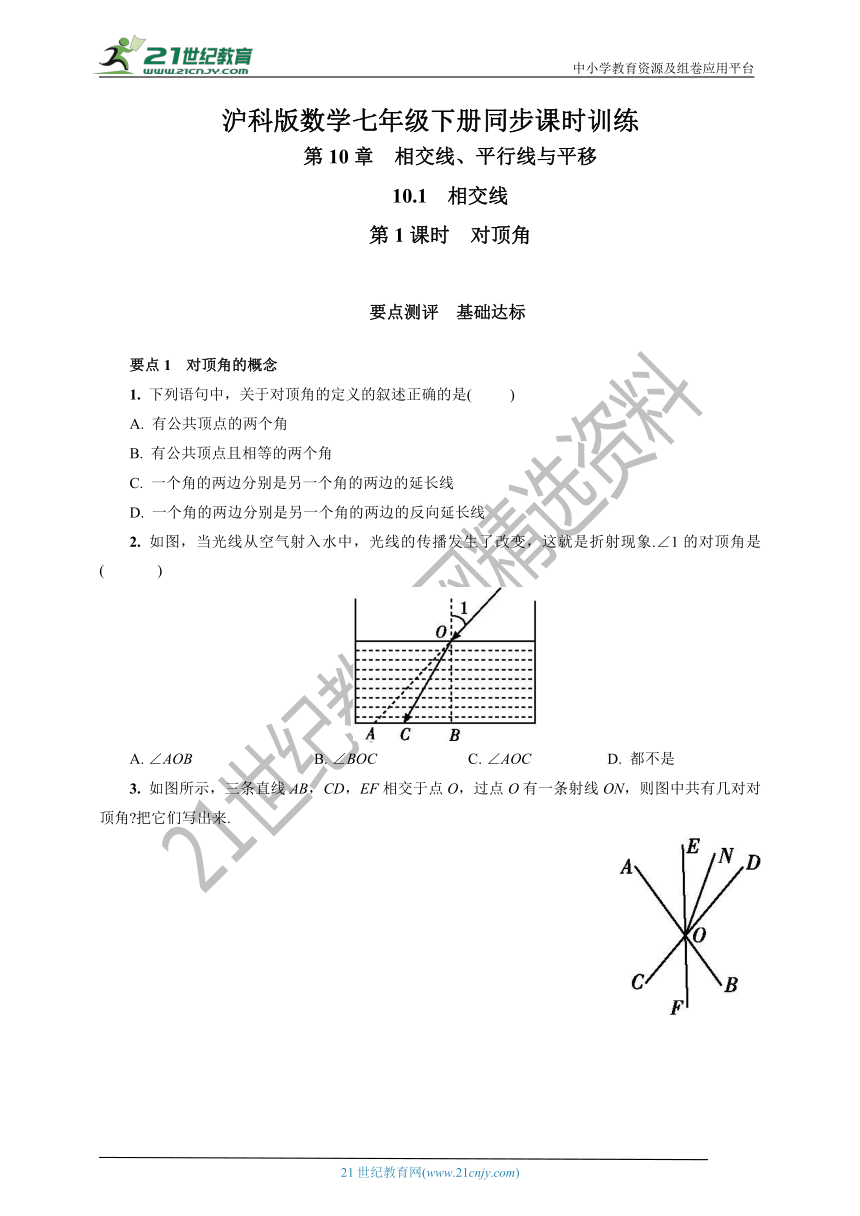
2. 如图,当光线从空气射入水中,光线的传播发生了改变,这就是折射现象.∠1的对顶角是( )
A. ∠AOB B. ∠BOC C. ∠AOC D. 都不是
3. 如图所示,三条直线AB,CD,EF相交于点O,过点O有一条射线ON,则图中共有几对对顶角?把它们写出来.
要点2 对顶角的性质
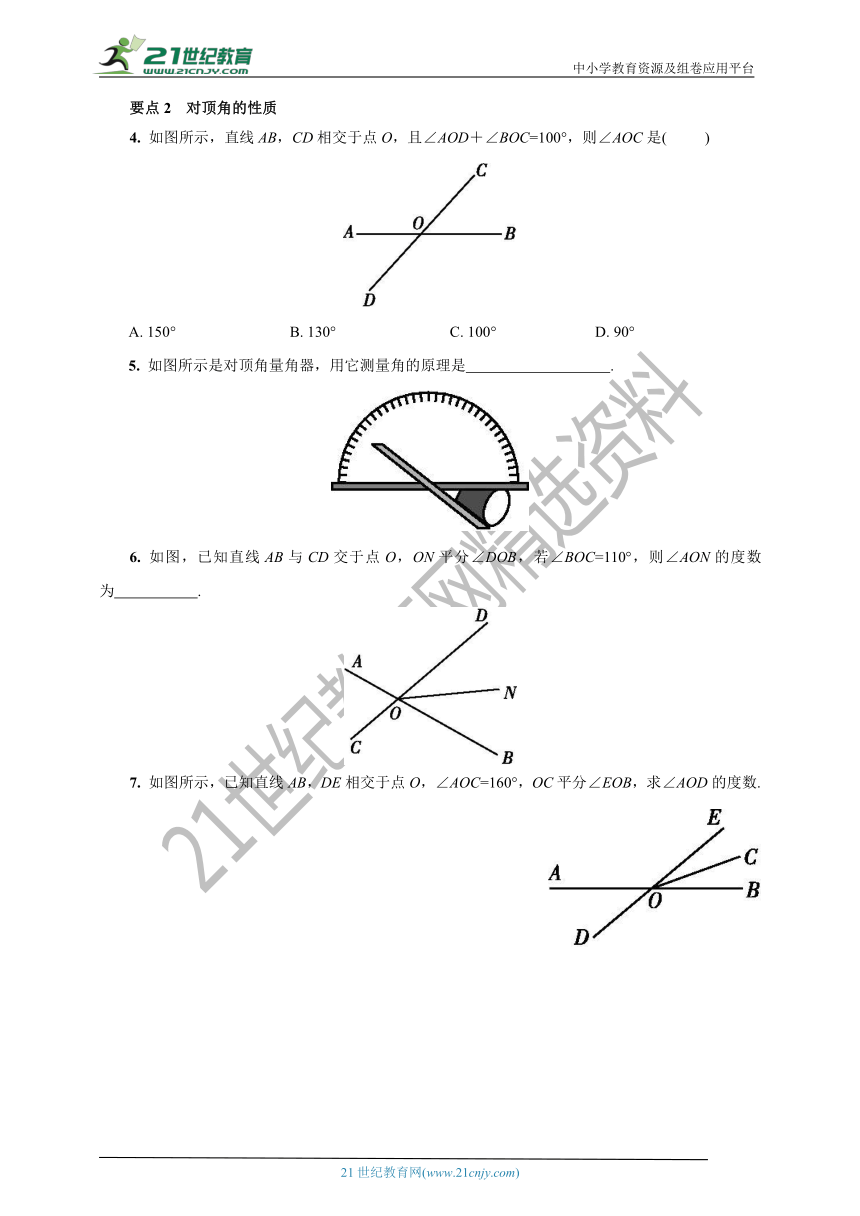
4. 如图所示,直线AB,CD相交于点O,且∠AOD+∠BOC=100°,则∠AOC是( )
A. 150° B. 130° C. 100° D. 90°
5. 如图所示是对顶角量角器,用它测量角的原理是 .?
6. 如图,已知直线AB与CD交于点O,ON平分∠DOB,若∠BOC=110°,则∠AON的度数为 .?
7. 如图所示,已知直线AB,DE相交于点O,∠AOC=160°,OC平分∠EOB,求∠AOD的度数.
课后集训 巩固提升
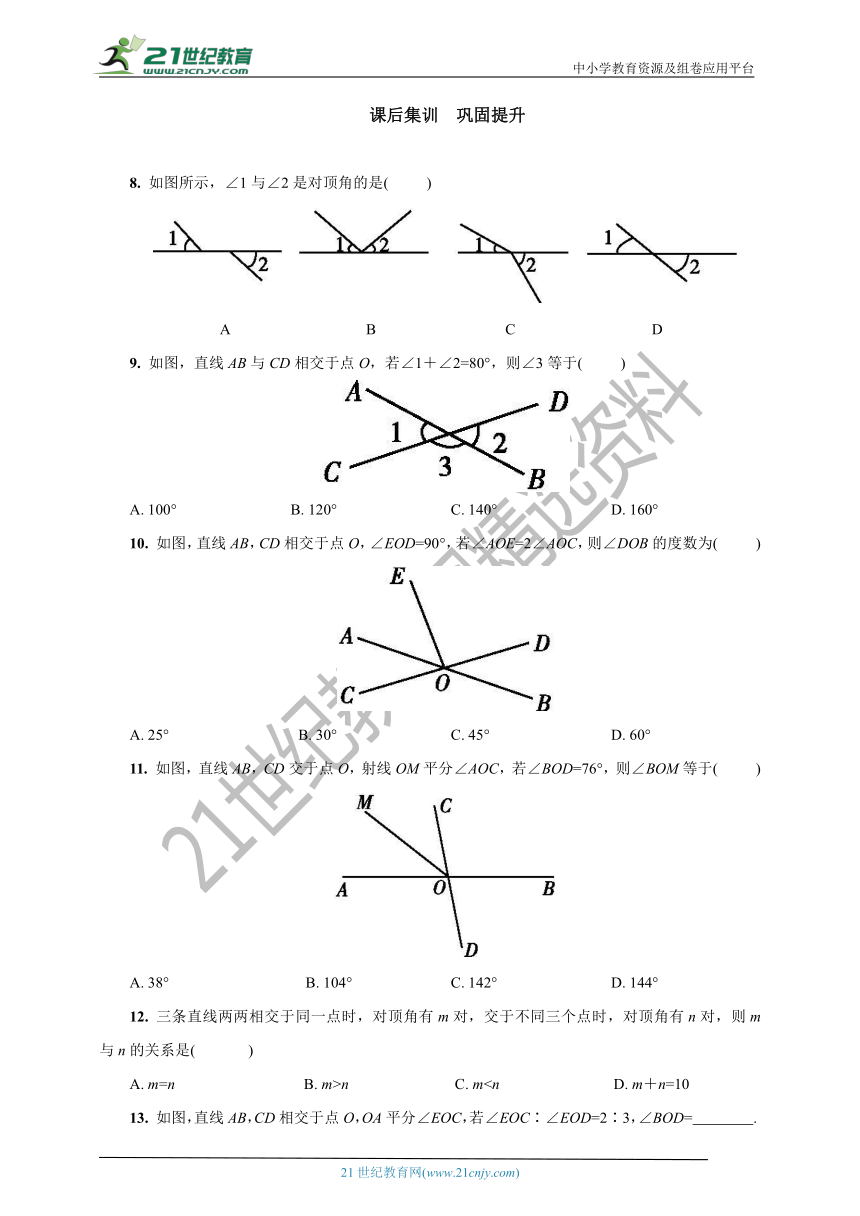
8. 如图所示,∠1与∠2是对顶角的是( )
A B C D
9. 如图,直线AB与CD相交于点O,若∠1+∠2=80°,则∠3等于( )
A. 100° B. 120° C. 140° D. 160°
10. 如图,直线AB,CD相交于点O,∠EOD=90°,若∠AOE=2∠AOC,则∠DOB的度数为( )
A. 25° B. 30° C. 45° D. 60°
11. 如图,直线AB,CD交于点O,射线OM平分∠AOC,若∠BOD=76°,则∠BOM等于( )
A. 38° B. 104° C. 142° D. 144°
12. 三条直线两两相交于同一点时,对顶角有m对,交于不同三个点时,对顶角有n对,则m与n的关系是( )
A. m=n B. m>n C. m13. 如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOC∶∠EOD=2∶3,∠BOD= .?
14. 如图,三条直线l1,l2,l3相交于点O,则∠1+∠2+∠3= .?
15. 如图,直线AB,CD,EF交于O点,若∠AOE=40°,∠DOF=30°,则∠BOC= .?
16. 如图所示,直线AB交CD于点O,OE平分∠BOD,OF平分∠COB,∠AOD∶∠EOD=4∶1,则∠AOF= .?
17. 如图,直线AB,CD交于点O,则∠BOD= .?
18. 直线AB,CD,EF相交于点O.
(1)请写出∠AOD,∠EOC的对顶角;
(2)已知∠AOC=50°,求∠BOD,∠COB的度数.
19. 观察下列各图,寻找对顶角(不含平角):
图1 图2 图3
(1)如图1,图中共有 对对顶角;?
(2)如图2,图中共有 对对顶角;?
(3)如图3,图中共有 对对顶角;?
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成 对对顶角;?
(5)若有2020条直线相交于一点,则可形成多少对对顶角?
参 考 答 案
1. D 2. A
3. 解:图中共有6对对顶角,它们分别是:直线AB,CD相交构成的两对对顶角:∠AOD和∠BOC,∠AOC和∠BOD;直线AB,EF相交构成的两对对顶角:∠AOE和∠BOF,∠AOF和∠BOE;直线CD,EF相交构成的两对对顶角:∠DOE和∠COF,∠DOF和∠COE.
4. B
5. 对顶角相等
6. 145°
7. 解:因为∠AOC=160°,所以∠COB=180°-∠AOC=20°,又因为OC平分∠EOB,所以∠BOE=2∠COB=40°,因为∠AOD与∠BOE是对顶角,所以∠AOD=∠BOE=40°.
8. D 9. C 10. B 11. C 12. A
13. 36°
14. 180°
15. 110°
16. 120°
17. 60°
18. 解:(1)∠AOD,∠EOC的对顶角分别为∠BOC,∠DOF.
(2)因为∠AOC=50°(已知),所以∠BOD=50°(对顶角相等),∠COB=180°-∠AOC=180°-50°=130°.
19. 解:(1)如题图1,图中共有1×2=2(对)对顶角.
(2)如题图2,图中共有2×3=6(对)对顶角.
(3)如题图3,图中共有3×4=12(对)对顶角.
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成n(n-1)(对)对顶角.
(5)若有2020条直线相交于一点,则可形成(2020-1)×2020=4078380(对)对顶角.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
沪科版数学七年级下册同步课时训练
第10章 相交线、平行线与平移
10.1 相交线
第1课时 对顶角
要点测评 基础达标
要点1 对顶角的概念
1. 下列语句中,关于对顶角的定义的叙述正确的是( )
A. 有公共顶点的两个角
B. 有公共顶点且相等的两个角
C. 一个角的两边分别是另一个角的两边的延长线
D. 一个角的两边分别是另一个角的两边的反向延长线
2. 如图,当光线从空气射入水中,光线的传播发生了改变,这就是折射现象.∠1的对顶角是( )
A. ∠AOB B. ∠BOC C. ∠AOC D. 都不是
3. 如图所示,三条直线AB,CD,EF相交于点O,过点O有一条射线ON,则图中共有几对对顶角?把它们写出来.
要点2 对顶角的性质
4. 如图所示,直线AB,CD相交于点O,且∠AOD+∠BOC=100°,则∠AOC是( )
A. 150° B. 130° C. 100° D. 90°
5. 如图所示是对顶角量角器,用它测量角的原理是 .?
6. 如图,已知直线AB与CD交于点O,ON平分∠DOB,若∠BOC=110°,则∠AON的度数为 .?
7. 如图所示,已知直线AB,DE相交于点O,∠AOC=160°,OC平分∠EOB,求∠AOD的度数.
课后集训 巩固提升
8. 如图所示,∠1与∠2是对顶角的是( )
A B C D
9. 如图,直线AB与CD相交于点O,若∠1+∠2=80°,则∠3等于( )
A. 100° B. 120° C. 140° D. 160°
10. 如图,直线AB,CD相交于点O,∠EOD=90°,若∠AOE=2∠AOC,则∠DOB的度数为( )
A. 25° B. 30° C. 45° D. 60°
11. 如图,直线AB,CD交于点O,射线OM平分∠AOC,若∠BOD=76°,则∠BOM等于( )
A. 38° B. 104° C. 142° D. 144°
12. 三条直线两两相交于同一点时,对顶角有m对,交于不同三个点时,对顶角有n对,则m与n的关系是( )
A. m=n B. m>n C. m
14. 如图,三条直线l1,l2,l3相交于点O,则∠1+∠2+∠3= .?
15. 如图,直线AB,CD,EF交于O点,若∠AOE=40°,∠DOF=30°,则∠BOC= .?
16. 如图所示,直线AB交CD于点O,OE平分∠BOD,OF平分∠COB,∠AOD∶∠EOD=4∶1,则∠AOF= .?
17. 如图,直线AB,CD交于点O,则∠BOD= .?
18. 直线AB,CD,EF相交于点O.
(1)请写出∠AOD,∠EOC的对顶角;
(2)已知∠AOC=50°,求∠BOD,∠COB的度数.
19. 观察下列各图,寻找对顶角(不含平角):
图1 图2 图3
(1)如图1,图中共有 对对顶角;?
(2)如图2,图中共有 对对顶角;?
(3)如图3,图中共有 对对顶角;?
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成 对对顶角;?
(5)若有2020条直线相交于一点,则可形成多少对对顶角?
参 考 答 案
1. D 2. A
3. 解:图中共有6对对顶角,它们分别是:直线AB,CD相交构成的两对对顶角:∠AOD和∠BOC,∠AOC和∠BOD;直线AB,EF相交构成的两对对顶角:∠AOE和∠BOF,∠AOF和∠BOE;直线CD,EF相交构成的两对对顶角:∠DOE和∠COF,∠DOF和∠COE.
4. B
5. 对顶角相等
6. 145°
7. 解:因为∠AOC=160°,所以∠COB=180°-∠AOC=20°,又因为OC平分∠EOB,所以∠BOE=2∠COB=40°,因为∠AOD与∠BOE是对顶角,所以∠AOD=∠BOE=40°.
8. D 9. C 10. B 11. C 12. A
13. 36°
14. 180°
15. 110°
16. 120°
17. 60°
18. 解:(1)∠AOD,∠EOC的对顶角分别为∠BOC,∠DOF.
(2)因为∠AOC=50°(已知),所以∠BOD=50°(对顶角相等),∠COB=180°-∠AOC=180°-50°=130°.
19. 解:(1)如题图1,图中共有1×2=2(对)对顶角.
(2)如题图2,图中共有2×3=6(对)对顶角.
(3)如题图3,图中共有3×4=12(对)对顶角.
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成n(n-1)(对)对顶角.
(5)若有2020条直线相交于一点,则可形成(2020-1)×2020=4078380(对)对顶角.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
