人教版九年级数学下册:《27.2.1 相似三角形的判定(二)》达标检测(含答案)
文档属性
| 名称 | 人教版九年级数学下册:《27.2.1 相似三角形的判定(二)》达标检测(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 110.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-23 00:00:00 | ||
图片预览


文档简介
《27.2.1 相似三角形的判定》达标检测
一、基础题
1.如图,在?ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF∽△CDE,则BF的长是( )
A.1.8 B.7.2 C.6.4 D.5
2.如图,已知△ABC,则下列4个三角形中,与△ABC相似的是( )
3.有甲、乙两个三角形木框,甲三角形木框的三边长分别为1,,,乙三角形木框的三边长分别为5,,,则甲、乙两个三角形( )
A.一定相似 B.一定不相似
C.无法判断 D.不一定相似
4.已知△ABC的三边长分别为,,2,△A′B′C′的两边长分别是1和,如果△ABC∽△A′B′C′,那么△A′B′C′的第三边长应该为( )
A. B. C. D.
5.下列三个三角形中相似的是( )
A.A与C B.A与B
C.B与C D.A,B,C都相似
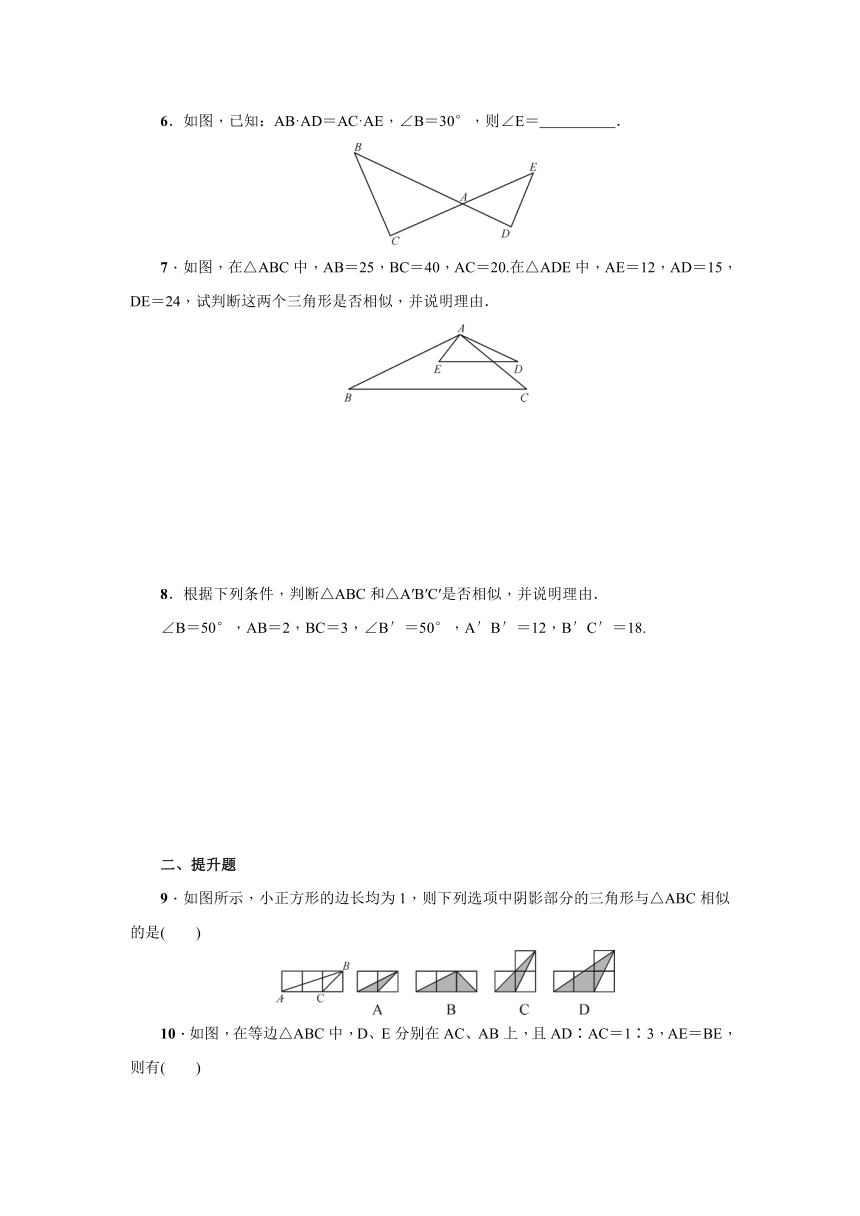
6.如图,已知:AB·AD=AC·AE,∠B=30°,则∠E= .
7.如图,在△ABC中,AB=25,BC=40,AC=20.在△ADE中,AE=12,AD=15,DE=24,试判断这两个三角形是否相似,并说明理由.
[来源:学科网]
8.根据下列条件,判断△ABC和△A′B′C′是否相似,并说明理由.
∠B=50°,AB=2,BC=3,∠B′=50°,A′B′=12,B′C′=18.
二、提升题
9.如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC相似的是( )
10.如图,在等边△ABC中,D、E分别在AC、AB上,且AD∶AC=1∶3,AE=BE,则有( )
A.△AED∽△ABD
B.△AED∽△BED
C.△AED∽△CBD
D.△BAD∽△BCD
11.一个钢筋三脚架三边长分别是20 cm、50 cm、60 cm.现在再做一个与其相似的钢筋三脚架,而只有长为30 cm和50 cm的两根钢筋,要求以其中一根为一边,从另一根上截下两段(允许有余料)作为两边,则下列截法:①将30 cm截出5 cm和25 cm;②将50 cm截出10 cm和25 cm;③将50 cm截出12 cm和36 cm;④将50 cm截出20 cm和30 cm.其中正确的有( )
A.1个 B.2个
C.3个 D.4个
12.如图,在△ABC中,AB=24,AC=18,D是AC上一点,AD=12,在AB上取一点E,使A、D、E三点组成的三角形与ABC相似,则AE= .
13.已知,在Rt△ABC中,∠C=90°,AB=10,BC=6.在Rt△EDF中,∠F=90°,DF=3,EF=4,则△ABC和△EDF相似吗?为什么?
14.如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且=.
(1)求证:△ADF∽△ACG;
(2)若=,求的值.
15.如图,Rt△ABC中,∠C=90°,AC=6 cm,BC=8 cm,动点P从点B出发,在BA边上以每秒5 cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4 cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.若以B,P,Q为顶点的三角形与△ABC相似,求t的值.
参考答案
一、基础题
1.A 2.C 3.A 4.D 5.A
6.30°
7.解:相似.
理由:∵==,==,
==,
∴==.
∴△ABC∽△ADE.
8.解:相似.理由:
∵==,==,
∴=.
∵∠B=∠B′,
∴△ABC∽△A′B′C′.
二、提升题
9.A 10.C 11.B
12.16或9
13.解:△ABC∽△EDF相似.理由如下:
在Rt△ABC中,∠C=90°,AB=10,BC=6,
根据勾股,得AC===8.
在Rt△EDF中,∠F=90°,DF=3,EF=4,
根据勾股,得ED===5.
在Rt△ABC和Rt△EDF中,==2,==2,==2,
∴==.
∴△ABC∽△EDF.
14.解:(1)证明:∵∠AED=∠B,∠DAE=∠BAC,
∴∠ADF=∠C.
又∵=,
∴△ADF∽△ACG.
(2)∵△ADF∽△ACG,
∴==.
∴=1.
15.解:由题意,得BP=5t,QC=4t,AB==10 cm.
①当△BPQ∽△BAC时,
则=,
∴=.解得t=1;
②当△BPQ∽△BCA时,则=,
∴=.解得t=.
综上所述,当t=1或时,以B,P,Q为顶点的三角形与△ABC相似.
一、基础题
1.如图,在?ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF∽△CDE,则BF的长是( )
A.1.8 B.7.2 C.6.4 D.5
2.如图,已知△ABC,则下列4个三角形中,与△ABC相似的是( )
3.有甲、乙两个三角形木框,甲三角形木框的三边长分别为1,,,乙三角形木框的三边长分别为5,,,则甲、乙两个三角形( )
A.一定相似 B.一定不相似
C.无法判断 D.不一定相似
4.已知△ABC的三边长分别为,,2,△A′B′C′的两边长分别是1和,如果△ABC∽△A′B′C′,那么△A′B′C′的第三边长应该为( )
A. B. C. D.
5.下列三个三角形中相似的是( )
A.A与C B.A与B
C.B与C D.A,B,C都相似
6.如图,已知:AB·AD=AC·AE,∠B=30°,则∠E= .
7.如图,在△ABC中,AB=25,BC=40,AC=20.在△ADE中,AE=12,AD=15,DE=24,试判断这两个三角形是否相似,并说明理由.
[来源:学科网]
8.根据下列条件,判断△ABC和△A′B′C′是否相似,并说明理由.
∠B=50°,AB=2,BC=3,∠B′=50°,A′B′=12,B′C′=18.
二、提升题
9.如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC相似的是( )
10.如图,在等边△ABC中,D、E分别在AC、AB上,且AD∶AC=1∶3,AE=BE,则有( )
A.△AED∽△ABD
B.△AED∽△BED
C.△AED∽△CBD
D.△BAD∽△BCD
11.一个钢筋三脚架三边长分别是20 cm、50 cm、60 cm.现在再做一个与其相似的钢筋三脚架,而只有长为30 cm和50 cm的两根钢筋,要求以其中一根为一边,从另一根上截下两段(允许有余料)作为两边,则下列截法:①将30 cm截出5 cm和25 cm;②将50 cm截出10 cm和25 cm;③将50 cm截出12 cm和36 cm;④将50 cm截出20 cm和30 cm.其中正确的有( )
A.1个 B.2个
C.3个 D.4个
12.如图,在△ABC中,AB=24,AC=18,D是AC上一点,AD=12,在AB上取一点E,使A、D、E三点组成的三角形与ABC相似,则AE= .
13.已知,在Rt△ABC中,∠C=90°,AB=10,BC=6.在Rt△EDF中,∠F=90°,DF=3,EF=4,则△ABC和△EDF相似吗?为什么?
14.如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且=.
(1)求证:△ADF∽△ACG;
(2)若=,求的值.
15.如图,Rt△ABC中,∠C=90°,AC=6 cm,BC=8 cm,动点P从点B出发,在BA边上以每秒5 cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4 cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.若以B,P,Q为顶点的三角形与△ABC相似,求t的值.
参考答案
一、基础题
1.A 2.C 3.A 4.D 5.A
6.30°
7.解:相似.
理由:∵==,==,
==,
∴==.
∴△ABC∽△ADE.
8.解:相似.理由:
∵==,==,
∴=.
∵∠B=∠B′,
∴△ABC∽△A′B′C′.
二、提升题
9.A 10.C 11.B
12.16或9
13.解:△ABC∽△EDF相似.理由如下:
在Rt△ABC中,∠C=90°,AB=10,BC=6,
根据勾股,得AC===8.
在Rt△EDF中,∠F=90°,DF=3,EF=4,
根据勾股,得ED===5.
在Rt△ABC和Rt△EDF中,==2,==2,==2,
∴==.
∴△ABC∽△EDF.
14.解:(1)证明:∵∠AED=∠B,∠DAE=∠BAC,
∴∠ADF=∠C.
又∵=,
∴△ADF∽△ACG.
(2)∵△ADF∽△ACG,
∴==.
∴=1.
15.解:由题意,得BP=5t,QC=4t,AB==10 cm.
①当△BPQ∽△BAC时,
则=,
∴=.解得t=1;
②当△BPQ∽△BCA时,则=,
∴=.解得t=.
综上所述,当t=1或时,以B,P,Q为顶点的三角形与△ABC相似.
