人教版九年级数学下册:《27.2.1 相似三角形的判定(三)》达标检测(含答案)
文档属性
| 名称 | 人教版九年级数学下册:《27.2.1 相似三角形的判定(三)》达标检测(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 95.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-23 11:28:21 | ||
图片预览


文档简介
《27.2.1 相似三角形的判定》达标检测
一、基础题
1.下列命题不一定成立的是( )
A.两个等腰直角三角形相似
B.各有一个角等于95°的两个等腰三角形相似
C.两边对应成比例且有一个角相等的两个三角形相似
D.斜边与一条直角边对应成比例的两个直角三角形相似
2.在△ABC和△A1B1C1中,∠A=∠A1=90°,添加下列条件不能判定两个三角形相似的是( )
A.∠B=∠B1 B.=
C.= D.=
3.有一个角为30°的两个直角三角形一定( )
A.相似 B.无法确定
C.全等 D.既全等又相似
4.如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于D点,则图中相似三角形有( )
A.1对 B.2对
C.3对 D.4对
5.在△ABC和△A′B′C′中,∠B=∠B′,下列条件不能判断这两个三角形相似的是( )
A.∠A=∠C′ B.=
C. ∠A=∠A′ D. =
6.在△ABC和△A′B′C′中,∠C=∠C′=90°,AC=12,AB=15,A′C′=8,则当A′B′= 时,△ABC∽△A′B′C′.
7.如图,锐角△ABC的边AB,AC上的高线CE,BF相交于点D,请写出图中的一对相似三角形 .(用相似符号连接)
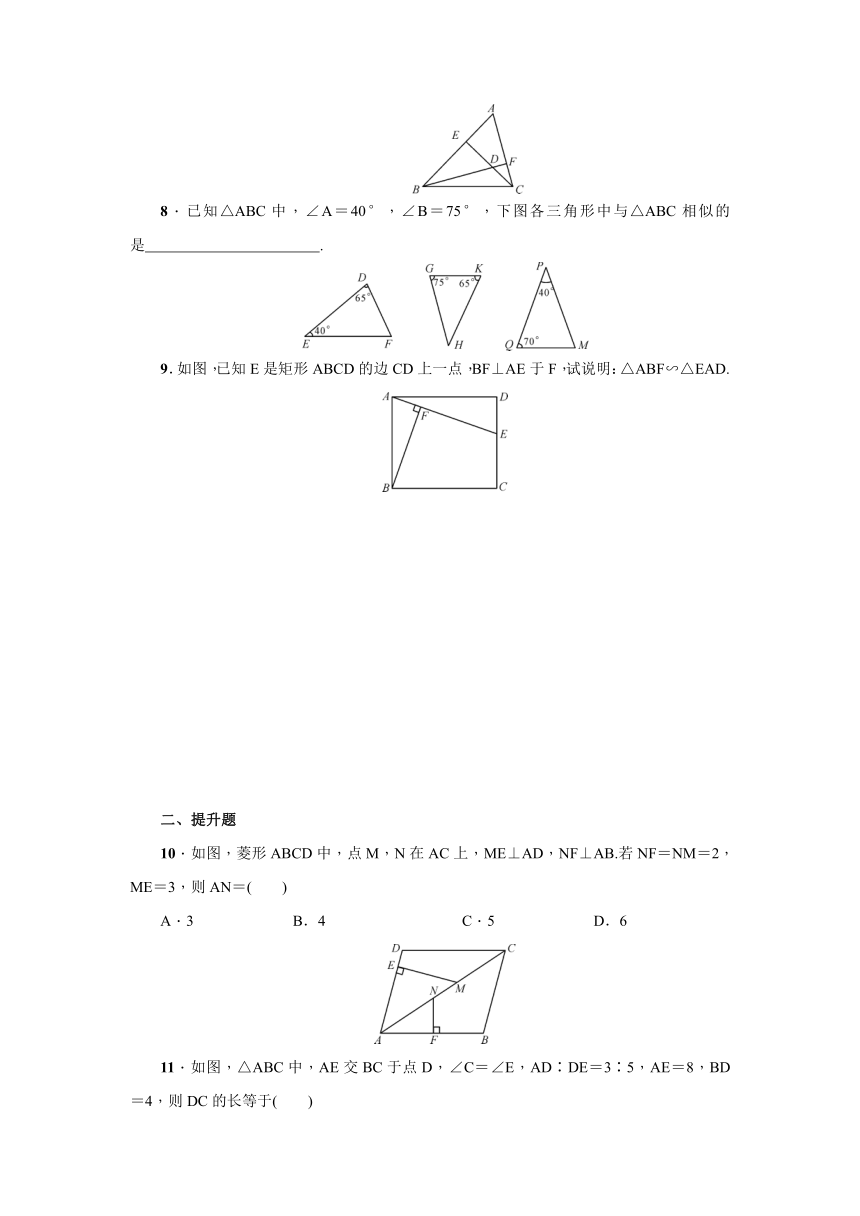
8.已知△ABC中,∠A=40°,∠B=75°,下图各三角形中与△ABC相似的是 .
9.如图,已知E是矩形ABCD的边CD上一点,BF⊥AE于F,试说明:△ABF∽△EAD.
二、提升题
10.如图,菱形ABCD中,点M,N在AC上,ME⊥AD,NF⊥AB.若NF=NM=2,ME=3,则AN=( )
A.3 B.4 C.5 D.6
11.如图,△ABC中,AE交BC于点D,∠C=∠E,AD∶DE=3∶5,AE=8,BD=4,则DC的长等于( )
A. B. C. D.
12.一个直角三角形的两边长分别为3和6,另一个直角三角形的两边长分别为2和4,那么这两个直角三角形 (填“一定”“不一定”或“一定不”)相似.
13.如图,已知∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是 .(只需写一个条件,不添加辅助线和字母)
14.如图,已知∠C=∠ABD=90°,AB=,AC=2,求AD的长为多少时,图中两直角三角形相似?
15.如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
(1)求证:△APQ∽△CDQ;
(2)P点从A点出发沿AB边以每秒1个单位长度的速度向B点移动,移动时间为t秒.当t为何值时,DP⊥AC?
16.如图,在?ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AE=6,求AF的长.
参考答案
一、基础题
1.C 2.D 3.A 4.C 5.D
6.10
7.答案不唯一,如△BDE∽△CDF,△ABF∽△ACE等
8.△EFD,△HGK
9.证明:∵矩形ABCD中,AB∥CD,∴∠BAF=∠AED.
∵BF⊥AE,∴∠AFB=90°.
∴∠AFB=∠D=90°.
∴△ABF∽△EAD.
二、提升题
10.B 11.A
12.不一定
13.答案不唯一,如AB∥DE
14.解:①若△ABC∽△ADB,
则=.
∴=.∴AD=3.
②若△ABC∽△DAB,
则=.∴=.
∴AD=3.
综上所述,当AD=3或3时,图中两直角三角形相似.
15.解:(1)证明:∵四边形ABCD是矩形,
∴AB∥CD.∴∠APQ=∠CDQ.
又∵∠AQP=∠CQD.
∴△APQ∽△CDQ.
(2)当t=5时,DP⊥AC.
理由:∵t=5,∴AP=5.∴=.
又∵=,∴=.
又∵∠PAD=∠ADC=90°,∴△PAD∽△ADC.
∴∠ADP=∠DCA.
∵∠ADP+∠CDP=∠ADC=90°,
∴∠DCA+∠CDP=90°.
∴∠DQC=90°,即DP⊥AC.
16.解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD.
∴∠ADF=∠CED,∠B+∠C=180°.
∵∠AFE+∠AFD=180°,∠AFE=∠B,
∴∠AFD=∠C.
∴△ADF∽△DEC.
(2)∵CD=AB=8,AE⊥BC,∴AE⊥AD.
在Rt△ADE中,DE==12.
∵△ADF∽△DEC,∴=.
∴=,解得AF=4.
一、基础题
1.下列命题不一定成立的是( )
A.两个等腰直角三角形相似
B.各有一个角等于95°的两个等腰三角形相似
C.两边对应成比例且有一个角相等的两个三角形相似
D.斜边与一条直角边对应成比例的两个直角三角形相似
2.在△ABC和△A1B1C1中,∠A=∠A1=90°,添加下列条件不能判定两个三角形相似的是( )
A.∠B=∠B1 B.=
C.= D.=
3.有一个角为30°的两个直角三角形一定( )
A.相似 B.无法确定
C.全等 D.既全等又相似
4.如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于D点,则图中相似三角形有( )
A.1对 B.2对
C.3对 D.4对
5.在△ABC和△A′B′C′中,∠B=∠B′,下列条件不能判断这两个三角形相似的是( )
A.∠A=∠C′ B.=
C. ∠A=∠A′ D. =
6.在△ABC和△A′B′C′中,∠C=∠C′=90°,AC=12,AB=15,A′C′=8,则当A′B′= 时,△ABC∽△A′B′C′.
7.如图,锐角△ABC的边AB,AC上的高线CE,BF相交于点D,请写出图中的一对相似三角形 .(用相似符号连接)
8.已知△ABC中,∠A=40°,∠B=75°,下图各三角形中与△ABC相似的是 .
9.如图,已知E是矩形ABCD的边CD上一点,BF⊥AE于F,试说明:△ABF∽△EAD.
二、提升题
10.如图,菱形ABCD中,点M,N在AC上,ME⊥AD,NF⊥AB.若NF=NM=2,ME=3,则AN=( )
A.3 B.4 C.5 D.6
11.如图,△ABC中,AE交BC于点D,∠C=∠E,AD∶DE=3∶5,AE=8,BD=4,则DC的长等于( )
A. B. C. D.
12.一个直角三角形的两边长分别为3和6,另一个直角三角形的两边长分别为2和4,那么这两个直角三角形 (填“一定”“不一定”或“一定不”)相似.
13.如图,已知∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是 .(只需写一个条件,不添加辅助线和字母)
14.如图,已知∠C=∠ABD=90°,AB=,AC=2,求AD的长为多少时,图中两直角三角形相似?
15.如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
(1)求证:△APQ∽△CDQ;
(2)P点从A点出发沿AB边以每秒1个单位长度的速度向B点移动,移动时间为t秒.当t为何值时,DP⊥AC?
16.如图,在?ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AE=6,求AF的长.
参考答案
一、基础题
1.C 2.D 3.A 4.C 5.D
6.10
7.答案不唯一,如△BDE∽△CDF,△ABF∽△ACE等
8.△EFD,△HGK
9.证明:∵矩形ABCD中,AB∥CD,∴∠BAF=∠AED.
∵BF⊥AE,∴∠AFB=90°.
∴∠AFB=∠D=90°.
∴△ABF∽△EAD.
二、提升题
10.B 11.A
12.不一定
13.答案不唯一,如AB∥DE
14.解:①若△ABC∽△ADB,
则=.
∴=.∴AD=3.
②若△ABC∽△DAB,
则=.∴=.
∴AD=3.
综上所述,当AD=3或3时,图中两直角三角形相似.
15.解:(1)证明:∵四边形ABCD是矩形,
∴AB∥CD.∴∠APQ=∠CDQ.
又∵∠AQP=∠CQD.
∴△APQ∽△CDQ.
(2)当t=5时,DP⊥AC.
理由:∵t=5,∴AP=5.∴=.
又∵=,∴=.
又∵∠PAD=∠ADC=90°,∴△PAD∽△ADC.
∴∠ADP=∠DCA.
∵∠ADP+∠CDP=∠ADC=90°,
∴∠DCA+∠CDP=90°.
∴∠DQC=90°,即DP⊥AC.
16.解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD.
∴∠ADF=∠CED,∠B+∠C=180°.
∵∠AFE+∠AFD=180°,∠AFE=∠B,
∴∠AFD=∠C.
∴△ADF∽△DEC.
(2)∵CD=AB=8,AE⊥BC,∴AE⊥AD.
在Rt△ADE中,DE==12.
∵△ADF∽△DEC,∴=.
∴=,解得AF=4.
