北师大版高中数学必修四第二章 平面向量2.4平面向量的坐标 课件(共18张PPT)
文档属性
| 名称 | 北师大版高中数学必修四第二章 平面向量2.4平面向量的坐标 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 804.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-24 09:10:26 | ||
图片预览





文档简介
(共18张PPT)
2.4平面向量的坐标
主讲:孙兴才
一、复习引入
1、平面向量基本定理
2、什么样的向量可以作为基底?
如果 e1 , e2是同一平面内的两个不共线的向量,那么对于这一平面内的任一向量 a ,有且只有一对实数 λ1 , λ2 使得a= λ1 e1+ λ2 e2
不共线的平面向量 e1 , e2 叫做这一平面内所有向量的一组基底.
二、平面向量的坐标表示
思考:
平面直角坐标系中,每一个点都可以用一对有序实数对表示,那对于平面直角坐标系中的每一个向量呢?
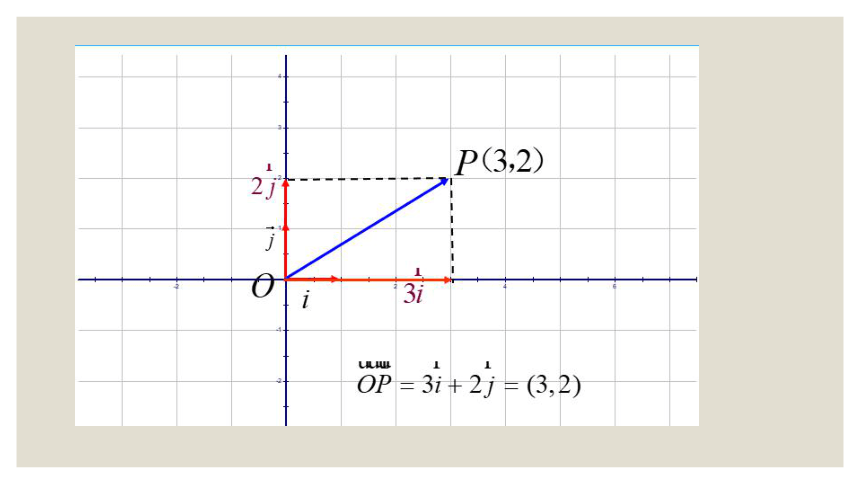
探索1
以O为起点,P为终点的向量能否用坐标表示?如何表示?
o
P
x
y
a
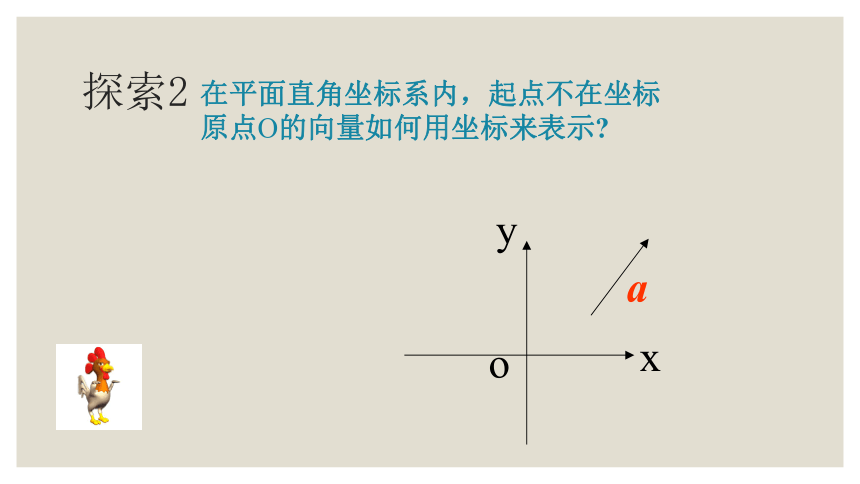
探索2
在平面直角坐标系内,起点不在坐标原点O的向量如何用坐标来表示?
o
x
y
a
可通过向量的平移,将向量的起点移到坐标的原点O处.
解决方案:
A
o
x
y
a
a
自由向量
教材:例1
三、平面向量线性运算的坐标表示
思考:平面向量可以用坐标表示,向量的运算可以用坐标来运算吗?如何计算?
(1)已知a =(x1 , y1), b= (x2 , y2) ,
求a + b , a – b .
(2)已知a =(x1 , y1)和实数 ,
求 a的坐标 .
两向量和与差的运算
实数与向量积的坐标运算
(1)两向量和与差的运算
已知,a=(x1,y1) , b=(x2,y2),
则
a+b=(x1i+y1j)+(x2i+y2j)
=(x1+x2)i+(y1+y2)j
即 a+b=(x1+x2,y1+y2)
同理可得 a-b=(x1-x2,y1-y2)
平面向量基本定理
这就是说,两个向量和与差的坐标分别等
于这两个向量相应坐标的和与差。
(2)实数与向量积的坐标运算
已知a=(x1,y1)和实数λ,那么
λ a= λ (x1i+y1j) = λ x1i+ λ y1j
即
λa=(λ x1, λ y1)
这就是说,实数与向量的积的坐标等用这个实数乘以原来向量的相应坐标。
教材:例2
结论:
一个向量的坐标等于表示此向量的有向线段的终点的坐标减去始点的坐标。 (末减初)
??向量的坐标和该向量的起点和终点的坐标有何关系?
如图,已知A(x1,y1),B(x2,y2),
则
AB= OB - OA
= (x2,y2) - (x1,y1)
= (x2-x1,y2-y1)
y
x
O
B(x2,y2)
A(x1,y1)
两向量和与差的坐标运算
教材:例3
四、向量平行的坐标表示
问题:如何用坐标表示两个共线向量?
提示:利用前面学习的向量共线的条件,把向量共线的条件转化为坐标表示
共线定理
设a、b是非零向量,且a=(x1,y1),b=(x2,y2),若 a//b,则存在存在实数λ,使a= λb,由平面向量基本定理知:
(x1i+y1j) =λ (x2i+y2j) = λ x2i+ λ y2j
即 x1= λx2
y1= λy2
消去λ后得
定理:教材90页
x1y2-x2y1=0
五、归纳总结
在平面直角坐标系内,我们分别取与X轴、Y轴方向相同的单位向量 i , j作为基底,任作一向量a,由平面向量基本定理知,有且仅有一对实数 x , y ,使得 a=x i+y j.
2 、把(x , y)叫做向量a的(直角)坐标,
记为:a=(x , y) , 称其为向量的坐标形式.
4、其中 x、 y 叫做 a 在X 、Y轴上的坐标.
单位向量 i =(1,0),j =(0,1)
1 、把 a=x i+y j 称为向量基底形式.
3、 a=x i+y j =( x , y)
5.加、减法法则.
a + b=( x2 , y2) + (x1 ,? y1)= (x2+x1 , y2+y1)
6.实数与向量积的运算法则:
λa =λ(x i+y j )=λx i+λy j =(λx , λy)
7.向量坐标.
若A(x1 , y1) , B(x2 , y2)
则 =(x2 - x1 , y2 – y1 )
a - b=( x2 , y2) - (x1 ,? y1)= (x2- x1 , y2-y1)
六、作业
教材练习:1、2、3
谢谢观赏
2.4平面向量的坐标
主讲:孙兴才
一、复习引入
1、平面向量基本定理
2、什么样的向量可以作为基底?
如果 e1 , e2是同一平面内的两个不共线的向量,那么对于这一平面内的任一向量 a ,有且只有一对实数 λ1 , λ2 使得a= λ1 e1+ λ2 e2
不共线的平面向量 e1 , e2 叫做这一平面内所有向量的一组基底.
二、平面向量的坐标表示
思考:
平面直角坐标系中,每一个点都可以用一对有序实数对表示,那对于平面直角坐标系中的每一个向量呢?
探索1
以O为起点,P为终点的向量能否用坐标表示?如何表示?
o
P
x
y
a
探索2
在平面直角坐标系内,起点不在坐标原点O的向量如何用坐标来表示?
o
x
y
a
可通过向量的平移,将向量的起点移到坐标的原点O处.
解决方案:
A
o
x
y
a
a
自由向量
教材:例1
三、平面向量线性运算的坐标表示
思考:平面向量可以用坐标表示,向量的运算可以用坐标来运算吗?如何计算?
(1)已知a =(x1 , y1), b= (x2 , y2) ,
求a + b , a – b .
(2)已知a =(x1 , y1)和实数 ,
求 a的坐标 .
两向量和与差的运算
实数与向量积的坐标运算
(1)两向量和与差的运算
已知,a=(x1,y1) , b=(x2,y2),
则
a+b=(x1i+y1j)+(x2i+y2j)
=(x1+x2)i+(y1+y2)j
即 a+b=(x1+x2,y1+y2)
同理可得 a-b=(x1-x2,y1-y2)
平面向量基本定理
这就是说,两个向量和与差的坐标分别等
于这两个向量相应坐标的和与差。
(2)实数与向量积的坐标运算
已知a=(x1,y1)和实数λ,那么
λ a= λ (x1i+y1j) = λ x1i+ λ y1j
即
λa=(λ x1, λ y1)
这就是说,实数与向量的积的坐标等用这个实数乘以原来向量的相应坐标。
教材:例2
结论:
一个向量的坐标等于表示此向量的有向线段的终点的坐标减去始点的坐标。 (末减初)
??向量的坐标和该向量的起点和终点的坐标有何关系?
如图,已知A(x1,y1),B(x2,y2),
则
AB= OB - OA
= (x2,y2) - (x1,y1)
= (x2-x1,y2-y1)
y
x
O
B(x2,y2)
A(x1,y1)
两向量和与差的坐标运算
教材:例3
四、向量平行的坐标表示
问题:如何用坐标表示两个共线向量?
提示:利用前面学习的向量共线的条件,把向量共线的条件转化为坐标表示
共线定理
设a、b是非零向量,且a=(x1,y1),b=(x2,y2),若 a//b,则存在存在实数λ,使a= λb,由平面向量基本定理知:
(x1i+y1j) =λ (x2i+y2j) = λ x2i+ λ y2j
即 x1= λx2
y1= λy2
消去λ后得
定理:教材90页
x1y2-x2y1=0
五、归纳总结
在平面直角坐标系内,我们分别取与X轴、Y轴方向相同的单位向量 i , j作为基底,任作一向量a,由平面向量基本定理知,有且仅有一对实数 x , y ,使得 a=x i+y j.
2 、把(x , y)叫做向量a的(直角)坐标,
记为:a=(x , y) , 称其为向量的坐标形式.
4、其中 x、 y 叫做 a 在X 、Y轴上的坐标.
单位向量 i =(1,0),j =(0,1)
1 、把 a=x i+y j 称为向量基底形式.
3、 a=x i+y j =( x , y)
5.加、减法法则.
a + b=( x2 , y2) + (x1 ,? y1)= (x2+x1 , y2+y1)
6.实数与向量积的运算法则:
λa =λ(x i+y j )=λx i+λy j =(λx , λy)
7.向量坐标.
若A(x1 , y1) , B(x2 , y2)
则 =(x2 - x1 , y2 – y1 )
a - b=( x2 , y2) - (x1 ,? y1)= (x2- x1 , y2-y1)
六、作业
教材练习:1、2、3
谢谢观赏
