湘教版九年级数学下册2.5直线与圆的位置关系同步测试及答案
文档属性
| 名称 | 湘教版九年级数学下册2.5直线与圆的位置关系同步测试及答案 |  | |
| 格式 | zip | ||
| 文件大小 | 157.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-24 09:07:03 | ||
图片预览



文档简介
2.5 直线与圆的位置关系
同步测试
1、选择题
1.△ABC中,∠C=90°,AB=13,AC=12,以B为圆心,5为半径的圆与直线AC的位置关系是( )
A.相切 B.相交 C.相离 D.不能确定
2.下列判断正确的是( )
①直线上一点到圆心的距离大于半径,则直线与圆相离;②直线上一点到圆心的距离等于半径,则直线与圆相切;③直线上一点到圆心的距离小于半径,则直线与圆相交.
A.①②③ B.①② C.②③ D.③
3.如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,连接OC,AC.若∠D=50°,则∠A的度数是( )
A.20° B.25° C.40° D.50°
4. 如图,PA、PB分别切⊙O于点A、B,AC是⊙O的直径,连结AB、BC、OP,
则与∠PAB相等的角(不包括∠PAB本身)有 ( )
A.1个 B.2个 C.3个 D.4个
5.一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于 ( )
A.21 B.20 C.19 D.18
6.如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为3的圆与OA的位置关系是( )
?
A.相离??? B.相交? ?C.相切?? D.以上三种情况均有可能
7.如图,图中实线部分是半径为9m的两条等弧组成的花坛,若每条弧所在的圆都经过另一个圆的圆心,则这个花坛的周长为( )
A.12πm???B.18πm???C.20πm???D.24πm
8.如图,直线AB与半径为2的⊙O相切于点C,点D,E,F是⊙O上三个点,EF∥AB,若EF=2 ,则∠EDC的度数为(?? )
A.?60°???B.?90°????C.?30°? ?D.?75°
9.如图,AB是半圆O的直径,C是半圆O上一点,CD是⊙O的切线,OD∥BC,OD与半圆O交于点E,则下列结论中不一定正确的是(?? )
A.AC⊥BC???B.BE平分∠ABC??C.BE∥CD??D.∠D=∠A
10..如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,点P是⊙A上的一点,且∠EPF=45°,则图中阴影部分的面积为(?? )
A. ?4﹣π????B.?4﹣2π???C.?8+π???D.?8﹣2π
二、填空题
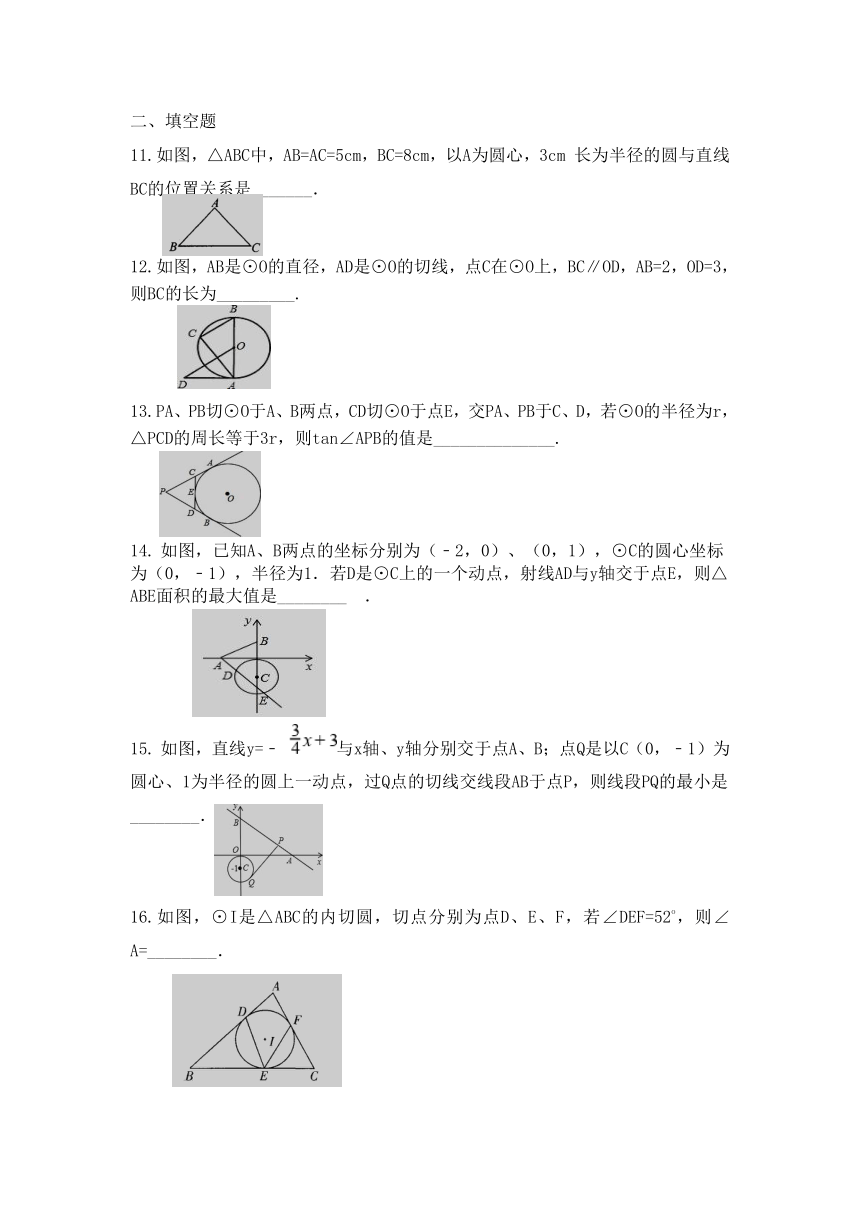
11.如图,△ABC中,AB=AC=5cm,BC=8cm,以A为圆心,3cm长为半径的圆与直线BC的位置关系是_______.
12.如图,AB是⊙O的直径,AD是⊙O的切线,点C在⊙O上,BC∥OD,AB=2,OD=3,则BC的长为_________.
13.PA、PB切⊙O于A、B两点,CD切⊙O于点E,交PA、PB于C、D,若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是______________.
14. 如图,已知A、B两点的坐标分别为(﹣2,0)、(0,1),⊙C的圆心坐标为(0,﹣1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是________?.
15. 如图,直线y=﹣ 与x轴、y轴分别交于点A、B;点Q是以C(0,﹣1)为圆心、1为半径的圆上一动点,过Q点的切线交线段AB于点P,则线段PQ的最小是________.
16.如图,⊙I是△ABC的内切圆,切点分别为点D、E、F,若∠DEF=52o,则∠A=________.
2、综合题
17.如图,AB为⊙O的直径,弦CD⊥AB于点M,过点B作BE∥CD,交AC的延长线于点E,连结BC.
(1)求证:BE为⊙O的切线;
(2)如果CD=6,tan∠BCD=,求⊙O的直径.
18. 如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,AE是⊙O的切线,∠CAE=60°.
(1)求∠D的度数;
(2)求证:AE是⊙O的切线;
(3)当BC=4时,求劣弧AC的长.
19.如图,在△ABC中,∠C=90°,AE平分∠BAC交BC于E,点O在AB上,以OA为半径的圆,交AB于D,交AC于C,且点E在⊙O上,连接DE,BF切⊙O于点F.
(1)求证:BE=BF;
(2)若⊙O的半径为R,AG=R+1,CE=R﹣1,求弦AG的长.
20.如图,A为半径18cm的⊙O上的定点,动点P从A出发,以3πcm/s的速发沿圆周按逆时针方向运动,当点P回到A地立即停止运动.
(1)如果∠POA=90°,求点P运动的时间;
(2)如果点B是OA延长线上的一点,AB=OA,那么当点P运动的时间为2s时.判断直线BP与⊙O的位置关系,并说明理由.
2.5 直线与圆的位置关系同步测试答案
1、选择题
1.B 2.D 3.A 4.C 5.D 6.C 7.D 8.C 9.C 10.A
二、填空题
11.相切
12.
13.
14.
15.
16.760
三、综合题
17.(1)∵CD⊥AB,BE∥CD,
∴EB⊥AB,
∵AB为圆的直径,
∴BE为圆O的切线;
(2)∵AB⊥CD,
∴M为CD中点,即CM=DM=CD=3,
在Rt△BCM中,tan∠BCD=,
即BM=3×=,
∵AB为圆O的直径,
∴∠BCA=90°,
∴∠BCD+∠ACD=90°,
∵∠ACD+∠CAB=90°,
∴∠BCD=∠CAB,
∴tan∠CAB=tan∠BCD=,
∴=,即AM=2CM=6,
则AB=AM+BM=6+=.
18. (1)∵∠ABC与∠ADC都是弧AC所对的圆周角,
∴∠ADC=∠B=60°.
(2)∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC=30°.
∴∠BAE=∠BAC+∠EAC=30°+60°=90°,即?BA⊥AE.
∴AE是⊙O的切线.
(3)如图,连接OC,
∴OB=OC,∠ABC=60°,
∴△OBC是等边三角形,∵OB=BC=4,∠BOC=60°,
∴∠AOC=120°,
∴劣弧AC的长为.
19. (1)证明:连接DG、OE,交于点H.
∵AE平分∠BAC交BC于E,
∴∠CAE=∠DAE,
∵OA=OE,
∴∠OAE=∠OEA,
∴∠CAE=∠OEA,
∴AC∥OE,
∴∠OEB=∠C=90°,
∴OE⊥BC,
∴BC是圆的切线,
∴BE=BF;
(2) AG=6
20. 解:(1)当∠POA=90°时,根据弧长公式可知点P运动的路程为⊙O周长的或,
设点P运动的时间为ts;
当点P运动的路程为⊙O周长的时,3π?t=?2π?18,
解得t=3;
当点P运动的路程为⊙O周长的时,3π?t=?2π?18,
解得t=9;
∴当∠POA=90°时,点P运动的时间为3s或9s.
(2)解:∵当OP⊥PB时,BP与⊙O相切,
∵AB=OA,OA=OP,
∴OB=2OP,∠OPB=90°;
∴∠B=30°;
∴∠O=60°;
∵OA=9cm,
∴弧AG==3π,
∴点P运动的距离为3π,
∴当t=1,有BP与⊙O相切.
同步测试
1、选择题
1.△ABC中,∠C=90°,AB=13,AC=12,以B为圆心,5为半径的圆与直线AC的位置关系是( )
A.相切 B.相交 C.相离 D.不能确定
2.下列判断正确的是( )
①直线上一点到圆心的距离大于半径,则直线与圆相离;②直线上一点到圆心的距离等于半径,则直线与圆相切;③直线上一点到圆心的距离小于半径,则直线与圆相交.
A.①②③ B.①② C.②③ D.③
3.如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,连接OC,AC.若∠D=50°,则∠A的度数是( )
A.20° B.25° C.40° D.50°
4. 如图,PA、PB分别切⊙O于点A、B,AC是⊙O的直径,连结AB、BC、OP,
则与∠PAB相等的角(不包括∠PAB本身)有 ( )
A.1个 B.2个 C.3个 D.4个
5.一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于 ( )
A.21 B.20 C.19 D.18
6.如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为3的圆与OA的位置关系是( )
?
A.相离??? B.相交? ?C.相切?? D.以上三种情况均有可能
7.如图,图中实线部分是半径为9m的两条等弧组成的花坛,若每条弧所在的圆都经过另一个圆的圆心,则这个花坛的周长为( )
A.12πm???B.18πm???C.20πm???D.24πm
8.如图,直线AB与半径为2的⊙O相切于点C,点D,E,F是⊙O上三个点,EF∥AB,若EF=2 ,则∠EDC的度数为(?? )
A.?60°???B.?90°????C.?30°? ?D.?75°
9.如图,AB是半圆O的直径,C是半圆O上一点,CD是⊙O的切线,OD∥BC,OD与半圆O交于点E,则下列结论中不一定正确的是(?? )
A.AC⊥BC???B.BE平分∠ABC??C.BE∥CD??D.∠D=∠A
10..如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,点P是⊙A上的一点,且∠EPF=45°,则图中阴影部分的面积为(?? )
A. ?4﹣π????B.?4﹣2π???C.?8+π???D.?8﹣2π
二、填空题
11.如图,△ABC中,AB=AC=5cm,BC=8cm,以A为圆心,3cm长为半径的圆与直线BC的位置关系是_______.
12.如图,AB是⊙O的直径,AD是⊙O的切线,点C在⊙O上,BC∥OD,AB=2,OD=3,则BC的长为_________.
13.PA、PB切⊙O于A、B两点,CD切⊙O于点E,交PA、PB于C、D,若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是______________.
14. 如图,已知A、B两点的坐标分别为(﹣2,0)、(0,1),⊙C的圆心坐标为(0,﹣1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是________?.
15. 如图,直线y=﹣ 与x轴、y轴分别交于点A、B;点Q是以C(0,﹣1)为圆心、1为半径的圆上一动点,过Q点的切线交线段AB于点P,则线段PQ的最小是________.
16.如图,⊙I是△ABC的内切圆,切点分别为点D、E、F,若∠DEF=52o,则∠A=________.
2、综合题
17.如图,AB为⊙O的直径,弦CD⊥AB于点M,过点B作BE∥CD,交AC的延长线于点E,连结BC.
(1)求证:BE为⊙O的切线;
(2)如果CD=6,tan∠BCD=,求⊙O的直径.
18. 如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,AE是⊙O的切线,∠CAE=60°.
(1)求∠D的度数;
(2)求证:AE是⊙O的切线;
(3)当BC=4时,求劣弧AC的长.
19.如图,在△ABC中,∠C=90°,AE平分∠BAC交BC于E,点O在AB上,以OA为半径的圆,交AB于D,交AC于C,且点E在⊙O上,连接DE,BF切⊙O于点F.
(1)求证:BE=BF;
(2)若⊙O的半径为R,AG=R+1,CE=R﹣1,求弦AG的长.
20.如图,A为半径18cm的⊙O上的定点,动点P从A出发,以3πcm/s的速发沿圆周按逆时针方向运动,当点P回到A地立即停止运动.
(1)如果∠POA=90°,求点P运动的时间;
(2)如果点B是OA延长线上的一点,AB=OA,那么当点P运动的时间为2s时.判断直线BP与⊙O的位置关系,并说明理由.
2.5 直线与圆的位置关系同步测试答案
1、选择题
1.B 2.D 3.A 4.C 5.D 6.C 7.D 8.C 9.C 10.A
二、填空题
11.相切
12.
13.
14.
15.
16.760
三、综合题
17.(1)∵CD⊥AB,BE∥CD,
∴EB⊥AB,
∵AB为圆的直径,
∴BE为圆O的切线;
(2)∵AB⊥CD,
∴M为CD中点,即CM=DM=CD=3,
在Rt△BCM中,tan∠BCD=,
即BM=3×=,
∵AB为圆O的直径,
∴∠BCA=90°,
∴∠BCD+∠ACD=90°,
∵∠ACD+∠CAB=90°,
∴∠BCD=∠CAB,
∴tan∠CAB=tan∠BCD=,
∴=,即AM=2CM=6,
则AB=AM+BM=6+=.
18. (1)∵∠ABC与∠ADC都是弧AC所对的圆周角,
∴∠ADC=∠B=60°.
(2)∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC=30°.
∴∠BAE=∠BAC+∠EAC=30°+60°=90°,即?BA⊥AE.
∴AE是⊙O的切线.
(3)如图,连接OC,
∴OB=OC,∠ABC=60°,
∴△OBC是等边三角形,∵OB=BC=4,∠BOC=60°,
∴∠AOC=120°,
∴劣弧AC的长为.
19. (1)证明:连接DG、OE,交于点H.
∵AE平分∠BAC交BC于E,
∴∠CAE=∠DAE,
∵OA=OE,
∴∠OAE=∠OEA,
∴∠CAE=∠OEA,
∴AC∥OE,
∴∠OEB=∠C=90°,
∴OE⊥BC,
∴BC是圆的切线,
∴BE=BF;
(2) AG=6
20. 解:(1)当∠POA=90°时,根据弧长公式可知点P运动的路程为⊙O周长的或,
设点P运动的时间为ts;
当点P运动的路程为⊙O周长的时,3π?t=?2π?18,
解得t=3;
当点P运动的路程为⊙O周长的时,3π?t=?2π?18,
解得t=9;
∴当∠POA=90°时,点P运动的时间为3s或9s.
(2)解:∵当OP⊥PB时,BP与⊙O相切,
∵AB=OA,OA=OP,
∴OB=2OP,∠OPB=90°;
∴∠B=30°;
∴∠O=60°;
∵OA=9cm,
∴弧AG==3π,
∴点P运动的距离为3π,
∴当t=1,有BP与⊙O相切.
