湘教版数学七年级下册 3.3 公式法——用平方差公式分解因式课件(共25张PPT)
文档属性
| 名称 | 湘教版数学七年级下册 3.3 公式法——用平方差公式分解因式课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-24 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
3.3 公式法
第1课时 用平方差公式因式分解
湘教版 七年级下册
学习目标
1.探索并运用平方差公式进行因式分解,体会转化
思想.(重点)
2.能会综合运用提公因式法和平方差公式对多项式进
行因式分解.(难点)
导入新课
a米
b米
b米
a米
(a-b)
情境引入
如图,在边长为a米的正方形上剪掉一个边长为b米的小正方形,将剩余部分拼成一个长方形,根据此图形变换,你能得到什么公式?
a2- b2=(a+b)(a-b)
1、平方差公式
(a+b)(a-b)=a2-b2
从左边到右边的这个过程叫___________.
整式乘法
2、反过来,a2-b2=__________.
(a+b)(a-b)
从左边到右边的这个过程叫___________.
分解因式
因此,a2-b2= (a+b)(a-b)是因式分解中的一个公式.
中首是( )
尾是( )
△2- 2=(△+ )(△- )
首2-尾2=(首+尾)(首-尾)
你对平方差公式认识有多深?
a2-b2=(a+b)(a-b)
√
√
×
×
辨一辨:下列多项式能否用平方差公式来分解因式,为什么?
√
√
★符合平方差的形式的多项式才能用平方差公式进行因式分解,即能写成: ( )2-( )2的形式.
两数是平方,
减号在中央.
(1)x2+y2
(2)x2-y2
(3)-x2-y2
-(x2+y2)
y2-x2
(4)-x2+y2
(5)x2-25y2
(x+5y)(x-5y)
(6)m2-1
(m+1)(m-1)
1、下列多项式能否用平方差公式来分解因式?
2.判断正误:
(1)x2+y2=(x+y)(x-y); ( )
(2) x2-y2=(x+y)(x-y); ( )
(3) -x2+y2=(-x+y)(-x-y); ( )
(4) -x2-y2=-(x+y)(x-y) . ( )
√
×
×
×
3. 填空:
(1)9y2 = ( )2;
±3y
不能
能
能
不能
如何把 x2-25 因式分解?
平方差公式(a+b)(a-b)= a2-b2,
把这个乘法公式从右到左地使用,得 a2-b2=(a+b)(a-b)
因此 x2-25
= x2-52
= (x+5)(x-5) .
a2-b2
= (a+b)(a-b) .
像上述例子那样,把乘法公式从右到左地使用,就可以用来把某些多项式分解因式.这种分解因式的方法叫做 公式法
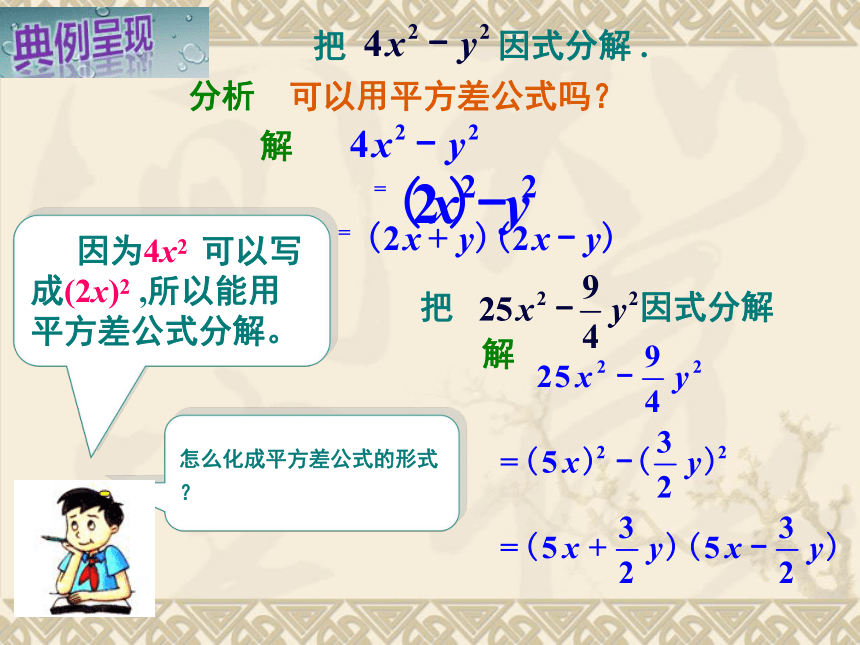
分析 可以用平方差公式吗?
因为4x2 可以写成(2x)2 ,所以能用平方差公式分解。
把 因式分解 .
=
解
=
把 因式分解
解
怎么化成平方差公式的形式?
把 因式分解.
解
把 因式分解: .
分析 可以用平方差公式吗?
因为 ,所以能用平方差公式分解.
解
=
=
=
注意:因式分解中必须进行到每个因式都不能分解为止.
1、下列多项式能否用平方差公式来分解因式?
2.判断正误:
(1)x2+y2=(x+y)(x-y); ( )
(2) x2-y2=(x+y)(x-y); ( )
(3) -x2+y2=(-x+y)(-x-y); ( )
(4) -x2-y2=-(x+y)(x-y) . ( )
√
×
×
×
3. 填空:
(1)9y2 = ( )2;
±3y
不能
能
能
不能
1. 把下列多项式因式分解:
(1)9y2-4x2;
(2)1-25x2
(4)(x+y)2-(y-x)2
(5)x4-16
(3y+2x)(3y-2x)
(1+5x)(1-5x)
4xy
(x2+4)(x+2)(x-2)
2. 计算:
(1)49.62-50.42;
(2)13.32-11.72.
= -80
= 40
(6) a4-16b4
( 7) (m-a)2-(n+b)2
(8) -16x4 + 81y4
(m-a+n+b)(m-a-n-b)
(3y+2x)(3y-2x)(9y2+4x2)
3. 手表表盘的外圆直径D=3.2cm,内圆直径d=2.8cm,
在外圆与内圆之间涂有防水材料.试求涂上防水材料
的圆环的面积(结果保留π).怎样计算较简便?
把x3y2-x5 因式分解.
解 x3y2-x5
= x3(y2-x2)
= x3(y+x)(y-x)
分析 : x3y2-x5有公因式 x3,应先提出公因式,再用公式进行因式分解.
问题:能直接用公式分解因式吗?
又如:把-4ax2+16ay2因式分解
解:-4ax2+16ay2
= -4a(x2-4y2)
=-4a(x+2y)(x-2y)
(4)a3-ab2
a(a+b)(a-b)
(3)9x4-36y2
9(x2+2y)(x2-2y)
1、分解因式: = .
2(x+2)(x-2)
(5) 25x4y2-x2
2、把下列各式因式分解
(6) 2a(x2+1)2-2ax2
x2(5xy+1)(5xy-1)
2a(x2+x+1)(x2-x+1)
3 已知x2-y2=-2,x+y=1,求x-y,x,y的值.
∴x-y=-2②.
解:∵x2-y2=(x+y)(x-y)=-2,
x+y=1①,
联立①②组成二元一次方程组,
解得
4 计算下列各题:
(1)1012-992; (2)53.52×4-46.52×4.
解:(1)原式=(101+99)(101-99)=400;
(2)原式=4(53.52-46.52)
=4(53.5+46.5)(53.5-46.5)
=4×100×7=2800.
方法总结:较为复杂的有理数运算,可以运用因式分解对其进行变形,使运算得以简化.
5 求证:当n为整数时,多项式(2n+1)2-(2n-1)2一定能被8整除.
即多项式(2n+1)2-(2n-1)2一定能被8整除.
证明:原式=(2n+1+2n-1)(2n+1-2n+1)=4n?2=8n,
∵n为整数,
∴8n被8整除,
方法总结:解决整除的基本思路就是将代数式化为整式乘积的形式,然后分析能被哪些数或式子整除.
1.下列多项式中能用平方差公式分解因式的是( )
A.a2+(-b)2 B.5m2-20mn
C.-x2-y2 D.-x2+9
当堂练习
D
2.分解因式(2x+3)2 -x2的结果是( )
A.3(x2+4x+3) B.3(x2+2x+3)
C.(3x+3)(x+3) D.3(x+1)(x+3)
D
3.若a+b=3,a-b=7,则b2-a2的值为( )
A.-21 B.21 C.-10 D.10
A
4.把下列各式分解因式:
(1) 16a2-9b2=_________________;
(2) (a+b)2-(a-b)2=_________________;
(3) 9xy3-36x3y=_________________;
(4) -a4+16=_________________.
(4a+3b)(4a-3b)
4ab
9xy(y+2x)(y-2x)
(4+a2)(2+a)(2-a)
5.若将(2x)n-81分解成(4x2+9)(2x+3)(2x-3),则n的值是_____________.
4
6.已知4m+n=40,2m-3n=5.求(m+2n)2-(3m-n)2的值.
原式=-40×5=-200.
解:原式=(m+2n+3m-n)(m+2n-3m+n)
=(4m+n)(3n-2m)
=-(4m+n)(2m-3n),
当4m+n=40,2m-3n=5时,
2、分解因式的步骤:
(1)、优先考虑提公因式法
(2)、其次看是否能用公式
(3)、两者都不行,综合运用两种方法
(4)、务必检查是否分解到底了
1、分解因式的方法
(1)提公因式法
(2)公式法:平方差公式
知识梳理
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
谢谢指导
3.3 公式法
第1课时 用平方差公式因式分解
湘教版 七年级下册
学习目标
1.探索并运用平方差公式进行因式分解,体会转化
思想.(重点)
2.能会综合运用提公因式法和平方差公式对多项式进
行因式分解.(难点)
导入新课
a米
b米
b米
a米
(a-b)
情境引入
如图,在边长为a米的正方形上剪掉一个边长为b米的小正方形,将剩余部分拼成一个长方形,根据此图形变换,你能得到什么公式?
a2- b2=(a+b)(a-b)
1、平方差公式
(a+b)(a-b)=a2-b2
从左边到右边的这个过程叫___________.
整式乘法
2、反过来,a2-b2=__________.
(a+b)(a-b)
从左边到右边的这个过程叫___________.
分解因式
因此,a2-b2= (a+b)(a-b)是因式分解中的一个公式.
中首是( )
尾是( )
△2- 2=(△+ )(△- )
首2-尾2=(首+尾)(首-尾)
你对平方差公式认识有多深?
a2-b2=(a+b)(a-b)
√
√
×
×
辨一辨:下列多项式能否用平方差公式来分解因式,为什么?
√
√
★符合平方差的形式的多项式才能用平方差公式进行因式分解,即能写成: ( )2-( )2的形式.
两数是平方,
减号在中央.
(1)x2+y2
(2)x2-y2
(3)-x2-y2
-(x2+y2)
y2-x2
(4)-x2+y2
(5)x2-25y2
(x+5y)(x-5y)
(6)m2-1
(m+1)(m-1)
1、下列多项式能否用平方差公式来分解因式?
2.判断正误:
(1)x2+y2=(x+y)(x-y); ( )
(2) x2-y2=(x+y)(x-y); ( )
(3) -x2+y2=(-x+y)(-x-y); ( )
(4) -x2-y2=-(x+y)(x-y) . ( )
√
×
×
×
3. 填空:
(1)9y2 = ( )2;
±3y
不能
能
能
不能
如何把 x2-25 因式分解?
平方差公式(a+b)(a-b)= a2-b2,
把这个乘法公式从右到左地使用,得 a2-b2=(a+b)(a-b)
因此 x2-25
= x2-52
= (x+5)(x-5) .
a2-b2
= (a+b)(a-b) .
像上述例子那样,把乘法公式从右到左地使用,就可以用来把某些多项式分解因式.这种分解因式的方法叫做 公式法
分析 可以用平方差公式吗?
因为4x2 可以写成(2x)2 ,所以能用平方差公式分解。
把 因式分解 .
=
解
=
把 因式分解
解
怎么化成平方差公式的形式?
把 因式分解.
解
把 因式分解: .
分析 可以用平方差公式吗?
因为 ,所以能用平方差公式分解.
解
=
=
=
注意:因式分解中必须进行到每个因式都不能分解为止.
1、下列多项式能否用平方差公式来分解因式?
2.判断正误:
(1)x2+y2=(x+y)(x-y); ( )
(2) x2-y2=(x+y)(x-y); ( )
(3) -x2+y2=(-x+y)(-x-y); ( )
(4) -x2-y2=-(x+y)(x-y) . ( )
√
×
×
×
3. 填空:
(1)9y2 = ( )2;
±3y
不能
能
能
不能
1. 把下列多项式因式分解:
(1)9y2-4x2;
(2)1-25x2
(4)(x+y)2-(y-x)2
(5)x4-16
(3y+2x)(3y-2x)
(1+5x)(1-5x)
4xy
(x2+4)(x+2)(x-2)
2. 计算:
(1)49.62-50.42;
(2)13.32-11.72.
= -80
= 40
(6) a4-16b4
( 7) (m-a)2-(n+b)2
(8) -16x4 + 81y4
(m-a+n+b)(m-a-n-b)
(3y+2x)(3y-2x)(9y2+4x2)
3. 手表表盘的外圆直径D=3.2cm,内圆直径d=2.8cm,
在外圆与内圆之间涂有防水材料.试求涂上防水材料
的圆环的面积(结果保留π).怎样计算较简便?
把x3y2-x5 因式分解.
解 x3y2-x5
= x3(y2-x2)
= x3(y+x)(y-x)
分析 : x3y2-x5有公因式 x3,应先提出公因式,再用公式进行因式分解.
问题:能直接用公式分解因式吗?
又如:把-4ax2+16ay2因式分解
解:-4ax2+16ay2
= -4a(x2-4y2)
=-4a(x+2y)(x-2y)
(4)a3-ab2
a(a+b)(a-b)
(3)9x4-36y2
9(x2+2y)(x2-2y)
1、分解因式: = .
2(x+2)(x-2)
(5) 25x4y2-x2
2、把下列各式因式分解
(6) 2a(x2+1)2-2ax2
x2(5xy+1)(5xy-1)
2a(x2+x+1)(x2-x+1)
3 已知x2-y2=-2,x+y=1,求x-y,x,y的值.
∴x-y=-2②.
解:∵x2-y2=(x+y)(x-y)=-2,
x+y=1①,
联立①②组成二元一次方程组,
解得
4 计算下列各题:
(1)1012-992; (2)53.52×4-46.52×4.
解:(1)原式=(101+99)(101-99)=400;
(2)原式=4(53.52-46.52)
=4(53.5+46.5)(53.5-46.5)
=4×100×7=2800.
方法总结:较为复杂的有理数运算,可以运用因式分解对其进行变形,使运算得以简化.
5 求证:当n为整数时,多项式(2n+1)2-(2n-1)2一定能被8整除.
即多项式(2n+1)2-(2n-1)2一定能被8整除.
证明:原式=(2n+1+2n-1)(2n+1-2n+1)=4n?2=8n,
∵n为整数,
∴8n被8整除,
方法总结:解决整除的基本思路就是将代数式化为整式乘积的形式,然后分析能被哪些数或式子整除.
1.下列多项式中能用平方差公式分解因式的是( )
A.a2+(-b)2 B.5m2-20mn
C.-x2-y2 D.-x2+9
当堂练习
D
2.分解因式(2x+3)2 -x2的结果是( )
A.3(x2+4x+3) B.3(x2+2x+3)
C.(3x+3)(x+3) D.3(x+1)(x+3)
D
3.若a+b=3,a-b=7,则b2-a2的值为( )
A.-21 B.21 C.-10 D.10
A
4.把下列各式分解因式:
(1) 16a2-9b2=_________________;
(2) (a+b)2-(a-b)2=_________________;
(3) 9xy3-36x3y=_________________;
(4) -a4+16=_________________.
(4a+3b)(4a-3b)
4ab
9xy(y+2x)(y-2x)
(4+a2)(2+a)(2-a)
5.若将(2x)n-81分解成(4x2+9)(2x+3)(2x-3),则n的值是_____________.
4
6.已知4m+n=40,2m-3n=5.求(m+2n)2-(3m-n)2的值.
原式=-40×5=-200.
解:原式=(m+2n+3m-n)(m+2n-3m+n)
=(4m+n)(3n-2m)
=-(4m+n)(2m-3n),
当4m+n=40,2m-3n=5时,
2、分解因式的步骤:
(1)、优先考虑提公因式法
(2)、其次看是否能用公式
(3)、两者都不行,综合运用两种方法
(4)、务必检查是否分解到底了
1、分解因式的方法
(1)提公因式法
(2)公式法:平方差公式
知识梳理
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
谢谢指导
