湘教版数学七年级下册3.2 提公因式 第一课时 公因式为单项式的提公因式法 课件(共22张PPT)
文档属性
| 名称 | 湘教版数学七年级下册3.2 提公因式 第一课时 公因式为单项式的提公因式法 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-23 12:02:17 | ||
图片预览







文档简介
(共22张PPT)
3.2 提公因式
第1课时 公因式为单项式的提公因式法
湘教版 七年级下册
学习目标
1.理解公因式及提公因式法的概念.(重点)
2.能运用提公因式法分解因式.(难点)
一、因式分解 :
像这样:ma+mb+mc=m(a+b+c)把一个多项式化成几个整式的积的形式,叫做因式分解
二、因式分解与整式乘法的关系:
(1)式:m(a+b+c)=ma+mb+mc是整式乘法
(2)式:ma+mb+mc=m(a+b+c)是因式分解
知识回顾
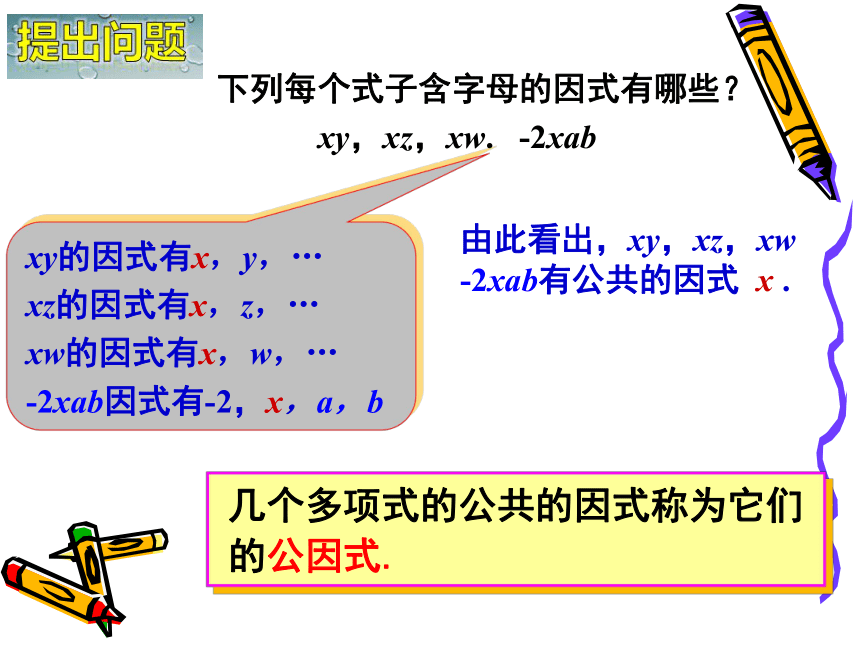
下列每个式子含字母的因式有哪些?
xy,xz,xw. -2xab
xy的因式有x,y,…
xz的因式有x,z,…
xw的因式有x,w,…
-2xab因式有-2,x,a,b
由此看出,xy,xz,xw
-2xab有公共的因式 x .
几个多项式的公共的因式称为它们的公因式.
找一找: 下列各多项式的公因式是什么?
3
a
a2
3mn
-2xy
(1) 3x+6y
(2)ab-2ac
(3) a 2 - a 3
(4)9 m 2n-6mn
(5)-6 x 2 y-8 xy 2
如何把多项式 xy+xz+xw 因式分解?
把乘法分配律从右到左地使用,便得出
xy+xz+xw=x(y+z+w).
像上面那样,如果一个多项式的各项有公因式,可以把这个公因式提到括号外面,这种把多项式因式分解的方法叫做提公因式法.
思考
提公因式法分解因式的理论依据是什么?
当多项式的某一项和公因式相同时,提公因式后剩余的项是1.
错误
注意:某项提出莫漏1.
解:原式 =x(3x-6y).
把3x2 - 6xy+x分解因式.
正确解:原式=3x·x-6y·x+1·x
=x(3x-6y+1)
小亮的解法有误吗?
把12x2y+18xy2分解因式.
解:原式 =3xy(4x + 6y).
错误
公因式没有提尽,还可以提出公因式2
注意:公因式要提尽.
正解:原式=6xy(2x+3y).
小明的解法有误吗?
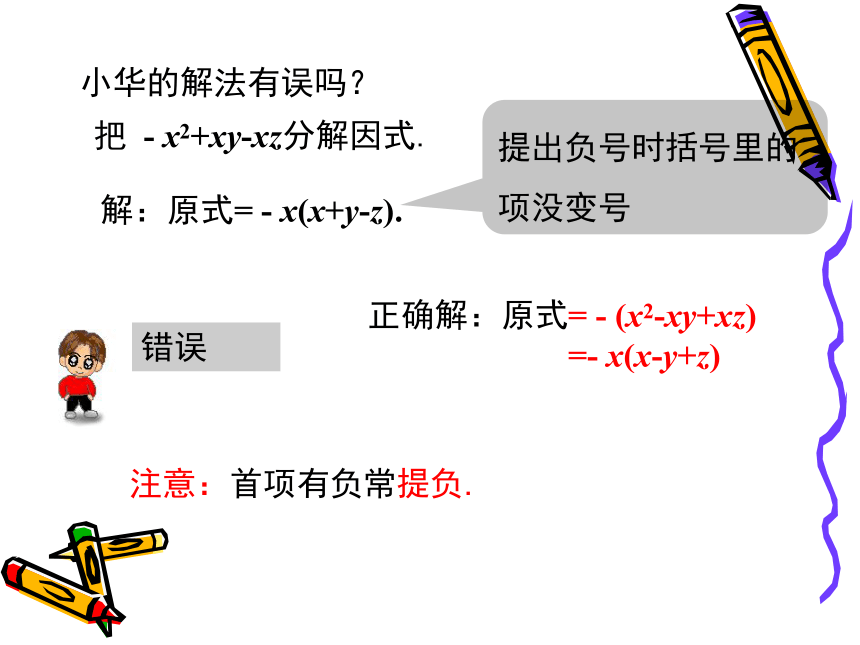
提出负号时括号里的项没变号
错误
把 - x2+xy-xz分解因式.
解:原式= - x(x+y-z).
注意:首项有负常提负.
正确解:原式= - (x2-xy+xz)
=- x(x-y+z)
小华的解法有误吗?
找多项式的公因式的方法
(1)系数——各项系数的最大公因数;
(2)字母——各项相同字母;
(3)指数——各项相同字母的最低次幂.
一看系数 二看字母 三看指数
归纳总结
解
注意例1中括号内的第3项为1
把 因式分解.
由于x = x · 1,因此x是x的因式.
由此看出,x是这个多项式各项的公因式.
分析 第3项的因式有哪些?
随堂演练
把 因式分解.
公因式里含字母吗?
公因式里含有字母x
例2
取各项系数的绝对值4,6的最大公因数2
第1项的系数为负,最好把负号提出,使括号内的第1项的系数为正.
分析: 公因式的系数如何确定?
由此看出,-2x是这个多项式的各项的公因式,把-2x提出后,括号内各项的系数如何计算?
解
注意同号两数相除得正数,异号两数相除得负数,因此把负号提出后,括号内的各项要变号.
用公因式的系数-2去除原来多项式的各项系数,所得的商就是括号内的各项系数.
把 因式分解.
公因式中含有哪些字母?它们的指数取多少?
4xy2 是公因式,把 4xy2 提出后,括号内的各项是什么样子?
公因式含的字母是各项中相同的字母x,y,它们的指数应当取它们在各项中次数最低的.
分析 公因式的系数如何确定?
是8与12的最大公因数4
由于第1项可以写成
因此括号内的第1项为 2xy2
解
由于第2项可以写成
因此括号内的第2项为 -3z
1. 说出下列多项式中各项的公因式:
公因式是3y.
(1)-12x2y+18xy-15y;
公因式是πr2.
公因式是 .
2. 在下列括号内填写适当的多项式:
(1)3x3-2x2+x= x( );
(2)-30x3y2+48x2yz = -6x2y ( ).
3x2-2x+1
5xy-8z
3. 把下列多项式因式分解:
y(3x-5y+1)
(1)3xy-5y2+y;
(4)-6m3n2-4m2n3+10m2n2.
-2m2n2(3m+2n-5)
4x2yz2 (x-2z2 +3x2yz)
(2) 8a 2c+ 2b c
(3)3 x3 -3x2 –9x
(5)-4a 3b3 +6 a2 b-2ab
(6) -2x2 –12xy2 +8xy3
2c(4a2+b)
3x(x2-x-3)
2ab(-2a2b2+3a-1)
2x(-x-6y2+4y3)
或-2ab(2a2b2-3a+1)
或-2x(x+6y2-4y3)
还有别的结果吗?
还有别的结果吗?
5.简便计算:
(1) 1.992+1.99×0.01 ;
(2)20132+2013-20142;
(3)(-2)101+(-2)100.
(2) 原式=2013(2013+1)-20142
=2013×2014-20142=2014×(2013-2014)
=-2014.
解:(1) 原式=1.99(1.99+0.01)=3.98;
(3)原式=(-2)100 ×(-2+1) =2100 ×(-1)=-2100.
6.已知: 2x+y=4,xy=3,求代数式2x2y+xy2的值.
解:2x2y+xy2=xy(2x+y)=3 ×4=12.
小结
几个多项式的公共的因式称为它们的公因式.
如果一个多项式的各项有公因式,可以把这个公因式提到括号外面,这种方法叫做提公因式法.
两步:第一步,找出公因式;第二步,提公因式.
注意:确定公因式的方法.
注意:
1、多项式是几项,提公因式后也剩几项.
2、当多项式的某一项和公因式相同时提公因式后剩余的项是1.
3、当多项式第一项系数是负数,通常先提出“-”号,使括号内第一项系数变为正数,注意括号内各项都要变号.
见《课堂内外》本课时练习
课后作业
谢谢,请提出宝贵意见!
3.2 提公因式
第1课时 公因式为单项式的提公因式法
湘教版 七年级下册
学习目标
1.理解公因式及提公因式法的概念.(重点)
2.能运用提公因式法分解因式.(难点)
一、因式分解 :
像这样:ma+mb+mc=m(a+b+c)把一个多项式化成几个整式的积的形式,叫做因式分解
二、因式分解与整式乘法的关系:
(1)式:m(a+b+c)=ma+mb+mc是整式乘法
(2)式:ma+mb+mc=m(a+b+c)是因式分解
知识回顾
下列每个式子含字母的因式有哪些?
xy,xz,xw. -2xab
xy的因式有x,y,…
xz的因式有x,z,…
xw的因式有x,w,…
-2xab因式有-2,x,a,b
由此看出,xy,xz,xw
-2xab有公共的因式 x .
几个多项式的公共的因式称为它们的公因式.
找一找: 下列各多项式的公因式是什么?
3
a
a2
3mn
-2xy
(1) 3x+6y
(2)ab-2ac
(3) a 2 - a 3
(4)9 m 2n-6mn
(5)-6 x 2 y-8 xy 2
如何把多项式 xy+xz+xw 因式分解?
把乘法分配律从右到左地使用,便得出
xy+xz+xw=x(y+z+w).
像上面那样,如果一个多项式的各项有公因式,可以把这个公因式提到括号外面,这种把多项式因式分解的方法叫做提公因式法.
思考
提公因式法分解因式的理论依据是什么?
当多项式的某一项和公因式相同时,提公因式后剩余的项是1.
错误
注意:某项提出莫漏1.
解:原式 =x(3x-6y).
把3x2 - 6xy+x分解因式.
正确解:原式=3x·x-6y·x+1·x
=x(3x-6y+1)
小亮的解法有误吗?
把12x2y+18xy2分解因式.
解:原式 =3xy(4x + 6y).
错误
公因式没有提尽,还可以提出公因式2
注意:公因式要提尽.
正解:原式=6xy(2x+3y).
小明的解法有误吗?
提出负号时括号里的项没变号
错误
把 - x2+xy-xz分解因式.
解:原式= - x(x+y-z).
注意:首项有负常提负.
正确解:原式= - (x2-xy+xz)
=- x(x-y+z)
小华的解法有误吗?
找多项式的公因式的方法
(1)系数——各项系数的最大公因数;
(2)字母——各项相同字母;
(3)指数——各项相同字母的最低次幂.
一看系数 二看字母 三看指数
归纳总结
解
注意例1中括号内的第3项为1
把 因式分解.
由于x = x · 1,因此x是x的因式.
由此看出,x是这个多项式各项的公因式.
分析 第3项的因式有哪些?
随堂演练
把 因式分解.
公因式里含字母吗?
公因式里含有字母x
例2
取各项系数的绝对值4,6的最大公因数2
第1项的系数为负,最好把负号提出,使括号内的第1项的系数为正.
分析: 公因式的系数如何确定?
由此看出,-2x是这个多项式的各项的公因式,把-2x提出后,括号内各项的系数如何计算?
解
注意同号两数相除得正数,异号两数相除得负数,因此把负号提出后,括号内的各项要变号.
用公因式的系数-2去除原来多项式的各项系数,所得的商就是括号内的各项系数.
把 因式分解.
公因式中含有哪些字母?它们的指数取多少?
4xy2 是公因式,把 4xy2 提出后,括号内的各项是什么样子?
公因式含的字母是各项中相同的字母x,y,它们的指数应当取它们在各项中次数最低的.
分析 公因式的系数如何确定?
是8与12的最大公因数4
由于第1项可以写成
因此括号内的第1项为 2xy2
解
由于第2项可以写成
因此括号内的第2项为 -3z
1. 说出下列多项式中各项的公因式:
公因式是3y.
(1)-12x2y+18xy-15y;
公因式是πr2.
公因式是 .
2. 在下列括号内填写适当的多项式:
(1)3x3-2x2+x= x( );
(2)-30x3y2+48x2yz = -6x2y ( ).
3x2-2x+1
5xy-8z
3. 把下列多项式因式分解:
y(3x-5y+1)
(1)3xy-5y2+y;
(4)-6m3n2-4m2n3+10m2n2.
-2m2n2(3m+2n-5)
4x2yz2 (x-2z2 +3x2yz)
(2) 8a 2c+ 2b c
(3)3 x3 -3x2 –9x
(5)-4a 3b3 +6 a2 b-2ab
(6) -2x2 –12xy2 +8xy3
2c(4a2+b)
3x(x2-x-3)
2ab(-2a2b2+3a-1)
2x(-x-6y2+4y3)
或-2ab(2a2b2-3a+1)
或-2x(x+6y2-4y3)
还有别的结果吗?
还有别的结果吗?
5.简便计算:
(1) 1.992+1.99×0.01 ;
(2)20132+2013-20142;
(3)(-2)101+(-2)100.
(2) 原式=2013(2013+1)-20142
=2013×2014-20142=2014×(2013-2014)
=-2014.
解:(1) 原式=1.99(1.99+0.01)=3.98;
(3)原式=(-2)100 ×(-2+1) =2100 ×(-1)=-2100.
6.已知: 2x+y=4,xy=3,求代数式2x2y+xy2的值.
解:2x2y+xy2=xy(2x+y)=3 ×4=12.
小结
几个多项式的公共的因式称为它们的公因式.
如果一个多项式的各项有公因式,可以把这个公因式提到括号外面,这种方法叫做提公因式法.
两步:第一步,找出公因式;第二步,提公因式.
注意:确定公因式的方法.
注意:
1、多项式是几项,提公因式后也剩几项.
2、当多项式的某一项和公因式相同时提公因式后剩余的项是1.
3、当多项式第一项系数是负数,通常先提出“-”号,使括号内第一项系数变为正数,注意括号内各项都要变号.
见《课堂内外》本课时练习
课后作业
谢谢,请提出宝贵意见!
