苏科版七年级数学下7.5多边形的内角和、外角和课件(3)(18张PPT)
文档属性
| 名称 | 苏科版七年级数学下7.5多边形的内角和、外角和课件(3)(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-23 00:00:00 | ||
图片预览


文档简介
(共18张PPT)
2020
§7.5多边形的内角和与外角和(3)
苏科版七年级下册 数学
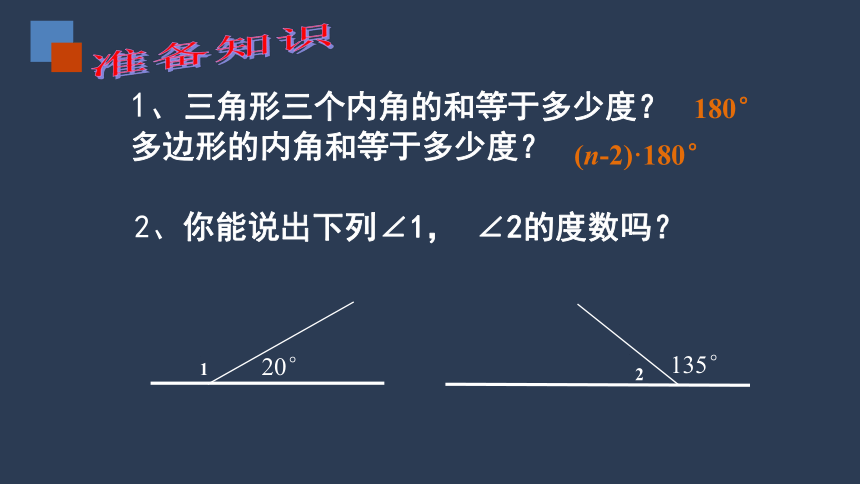
1、三角形三个内角的和等于多少度?多边形的内角和等于多少度?
2、你能说出下列∠1, ∠2的度数吗?
180°
(n-2)·180°
1
2
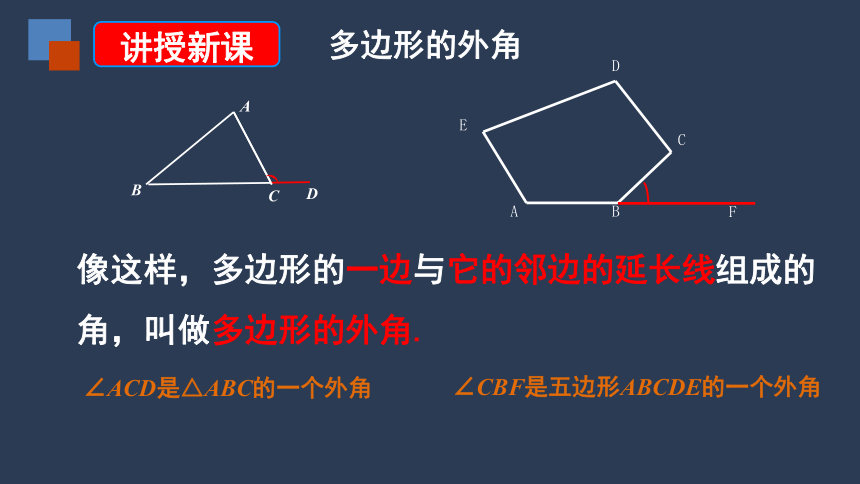
像这样,多边形的一边与它的邻边的延长线组成的角,叫做多边形的外角.
∠ACD是△ABC的一个外角
讲授新课
∠CBF是五边形ABCDE的一个外角
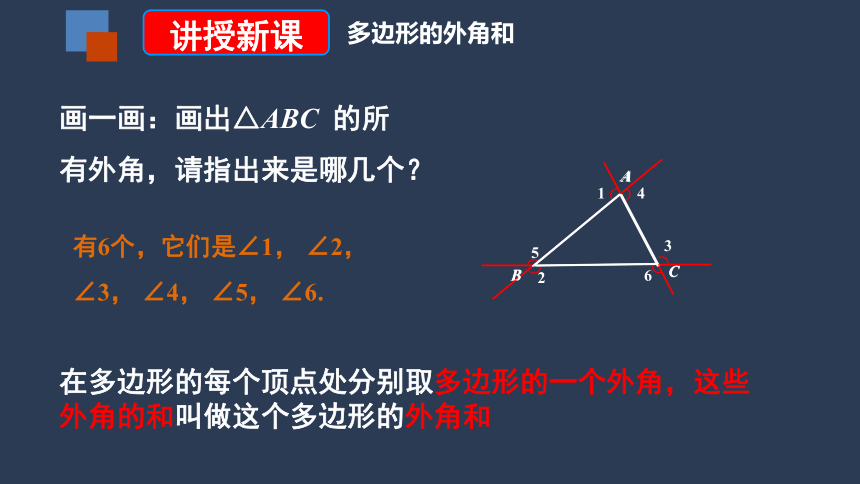
画一画:画出△ABC 的所有外角,请指出来是哪几个?
有6个,它们是∠1, ∠2, ∠3, ∠4, ∠5, ∠6.
在多边形的每个顶点处分别取多边形的一个外角,这些外角的和叫做这个多边形的外角和
讲授新课
多边形的外角和
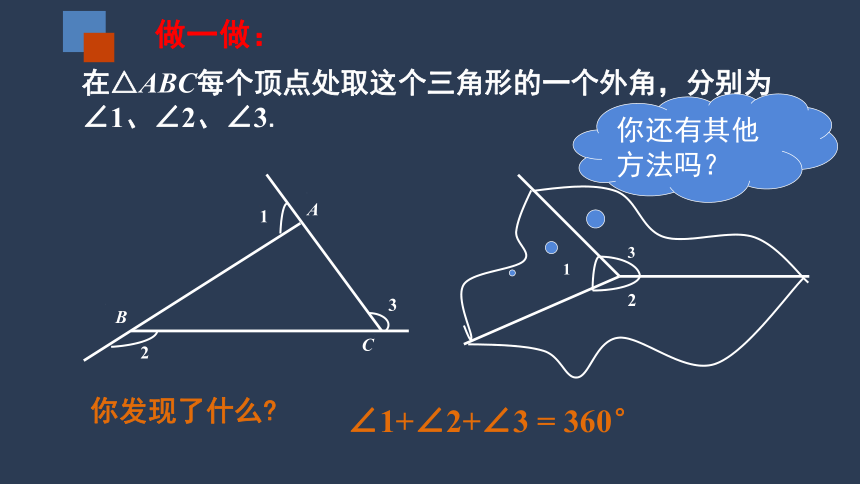
在△ABC每个顶点处取这个三角形的一个外角,分别为∠1、∠2、∠3.
做一做:
你发现了什么?
∠1+∠2+∠3 = 360°
你还有其他方法吗?
1
2
3
1
2
3
A
B
C
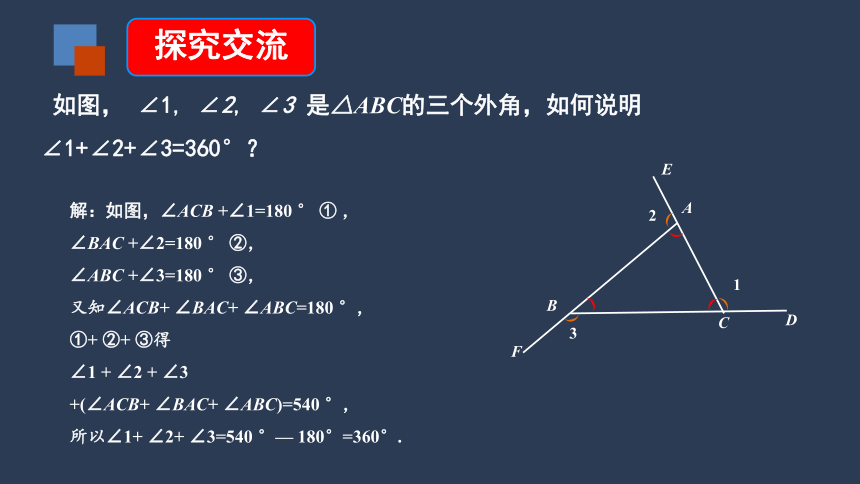
如图, ∠1, ∠2, ∠3 是△ABC的三个外角,如何说明∠1+∠2+∠3=360°?
探究交流
解:如图,∠ACB +∠1=180 ° ① ,
∠BAC +∠2=180 ° ②,
∠ABC +∠3=180 ° ③,
又知∠ACB+ ∠BAC+ ∠ABC=180 °,
①+ ②+ ③得
∠1 + ∠2 + ∠3
+(∠ACB+ ∠BAC+ ∠ABC)=540 °,
所以∠1+ ∠2+ ∠3=540 °— 180°=360°.
四边形的外角和等于多少度?
∵∠5+∠1=180°,
∠6+∠2=180°,
∠7+∠3=180°,
∠8+∠4=180°,
又∵∠1+∠2+∠3+ ∠4 = 180°×2
则∠5+∠6+∠7+∠8 =
360°
你能用上面的方法求出五边形的外角和吗?
猜想:n边形的外角和等于多少度?
结论:任意多边形的外角和都等于360°.
多边形外角和:
n·180°- (n-2)·180°=
n·180°- n·180°+360°=360°
∠1+∠2+∠3+∠4+∠5=360°
试一试:
1. 如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____.
12
2. 已知一个多边形,它的内角和等于外角和的2倍,则这个多边形的边数为 .
6
3. 多边形边数增加一条,则它的内角和增加
度,外角和 .
180
不变
360°÷30°=12
(n-2)·180°=n·150°
(n-2)·180°=360°×2
例1:求出下列图形中∠1和∠2的度数:
∵△ABC中 ,∠A+∠B+∠1=180°
又∵∠A=80°,∠B=60°
∴∠1=40°
∵∠1+∠2=180°
∴∠2=140 °
∠2=130 °,∠1=18 °
D
例2、如图,小明从点A出发沿直线前进10m到达点B,向左转30°后又沿直线前进10m到达点C,再向左转30°后沿直线前进10m到达点D……照这样走下去,
小明第一次回到出发点A,一
共走了多少米?
B
A
C
D
解:360°÷30°=12
12×10=120米
答:小明一共走了120米。
1.一个多边形,它的外角最多有几个是钝角?说说你的理由.
拓展提升:
分析:钝角是大于90?的角,若是4个钝角,则外角和就超过360?.
2一个多边形,小于108?的内角最多有几个?说说你的理由.
分析:因为内角若小于108?,则相应的外角就大于72?,在多边形中,大于72?的外角最多有4个.
(若是5个大于72?的外角,则外角和超过360?)
最多有3个.
最多有4个.
从四边形纸片中剪去一个三角形,剩余的部分是几边形?此时,多边形的内角和与外角和分别是多少?
剪去一个三角形后,剩下的多边形分3种情况:
五边形
四边形
三角形
议一议:
变式:从五边形纸片中剪去一个三角形,剩余的部分是几边形?此时,多边形的内角和与外角和分别是多少?
剪去一个三角形后,剩下的多边形分3种情况:
六边形
五边形
四边形
结论:n边形减去一个三角形后,剩余部分得到的是:
①(n-1)边形、②n 边形、 ③(n+1)边形
课堂小结
多边形的外角
多边形的外角和
三角形的外角和等于360 °
多边形的外角和等于360°
由特殊到一般
类比思想
方法归纳
多边形的一边与它的邻边的延长线组成的角,叫做多边形的外角.
布置作业:
1. 一个五边形五个外角的比是2:3:4:5:6,则这个五边形五个外角的度数分别是 .
2.一个多边形的每一个外角都是72?,则这个多边形的内角和是 .
3.一个多边形的每一个内角都是150?,则这个多边形是
几边形?你有几种不同的思考方法?(请写出过程)
4.一个多边形的内角和与外角和的总和为1800°,求这个多边形的边数.
5.如果一个多边形的内角和与外角和之比是13:2,求这个多边形的边数.
6.如图,D是△ABC的边BC上一点,∠B=∠BAD,
∠C=∠ADC , ∠DAC=40?. 求:∠B的度数
A
B
C
D
40 ?
A
B
C
D
谢谢
祝好!
2020
§7.5多边形的内角和与外角和(3)
苏科版七年级下册 数学
1、三角形三个内角的和等于多少度?多边形的内角和等于多少度?
2、你能说出下列∠1, ∠2的度数吗?
180°
(n-2)·180°
1
2
像这样,多边形的一边与它的邻边的延长线组成的角,叫做多边形的外角.
∠ACD是△ABC的一个外角
讲授新课
∠CBF是五边形ABCDE的一个外角
画一画:画出△ABC 的所有外角,请指出来是哪几个?
有6个,它们是∠1, ∠2, ∠3, ∠4, ∠5, ∠6.
在多边形的每个顶点处分别取多边形的一个外角,这些外角的和叫做这个多边形的外角和
讲授新课
多边形的外角和
在△ABC每个顶点处取这个三角形的一个外角,分别为∠1、∠2、∠3.
做一做:
你发现了什么?
∠1+∠2+∠3 = 360°
你还有其他方法吗?
1
2
3
1
2
3
A
B
C
如图, ∠1, ∠2, ∠3 是△ABC的三个外角,如何说明∠1+∠2+∠3=360°?
探究交流
解:如图,∠ACB +∠1=180 ° ① ,
∠BAC +∠2=180 ° ②,
∠ABC +∠3=180 ° ③,
又知∠ACB+ ∠BAC+ ∠ABC=180 °,
①+ ②+ ③得
∠1 + ∠2 + ∠3
+(∠ACB+ ∠BAC+ ∠ABC)=540 °,
所以∠1+ ∠2+ ∠3=540 °— 180°=360°.
四边形的外角和等于多少度?
∵∠5+∠1=180°,
∠6+∠2=180°,
∠7+∠3=180°,
∠8+∠4=180°,
又∵∠1+∠2+∠3+ ∠4 = 180°×2
则∠5+∠6+∠7+∠8 =
360°
你能用上面的方法求出五边形的外角和吗?
猜想:n边形的外角和等于多少度?
结论:任意多边形的外角和都等于360°.
多边形外角和:
n·180°- (n-2)·180°=
n·180°- n·180°+360°=360°
∠1+∠2+∠3+∠4+∠5=360°
试一试:
1. 如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____.
12
2. 已知一个多边形,它的内角和等于外角和的2倍,则这个多边形的边数为 .
6
3. 多边形边数增加一条,则它的内角和增加
度,外角和 .
180
不变
360°÷30°=12
(n-2)·180°=n·150°
(n-2)·180°=360°×2
例1:求出下列图形中∠1和∠2的度数:
∵△ABC中 ,∠A+∠B+∠1=180°
又∵∠A=80°,∠B=60°
∴∠1=40°
∵∠1+∠2=180°
∴∠2=140 °
∠2=130 °,∠1=18 °
D
例2、如图,小明从点A出发沿直线前进10m到达点B,向左转30°后又沿直线前进10m到达点C,再向左转30°后沿直线前进10m到达点D……照这样走下去,
小明第一次回到出发点A,一
共走了多少米?
B
A
C
D
解:360°÷30°=12
12×10=120米
答:小明一共走了120米。
1.一个多边形,它的外角最多有几个是钝角?说说你的理由.
拓展提升:
分析:钝角是大于90?的角,若是4个钝角,则外角和就超过360?.
2一个多边形,小于108?的内角最多有几个?说说你的理由.
分析:因为内角若小于108?,则相应的外角就大于72?,在多边形中,大于72?的外角最多有4个.
(若是5个大于72?的外角,则外角和超过360?)
最多有3个.
最多有4个.
从四边形纸片中剪去一个三角形,剩余的部分是几边形?此时,多边形的内角和与外角和分别是多少?
剪去一个三角形后,剩下的多边形分3种情况:
五边形
四边形
三角形
议一议:
变式:从五边形纸片中剪去一个三角形,剩余的部分是几边形?此时,多边形的内角和与外角和分别是多少?
剪去一个三角形后,剩下的多边形分3种情况:
六边形
五边形
四边形
结论:n边形减去一个三角形后,剩余部分得到的是:
①(n-1)边形、②n 边形、 ③(n+1)边形
课堂小结
多边形的外角
多边形的外角和
三角形的外角和等于360 °
多边形的外角和等于360°
由特殊到一般
类比思想
方法归纳
多边形的一边与它的邻边的延长线组成的角,叫做多边形的外角.
布置作业:
1. 一个五边形五个外角的比是2:3:4:5:6,则这个五边形五个外角的度数分别是 .
2.一个多边形的每一个外角都是72?,则这个多边形的内角和是 .
3.一个多边形的每一个内角都是150?,则这个多边形是
几边形?你有几种不同的思考方法?(请写出过程)
4.一个多边形的内角和与外角和的总和为1800°,求这个多边形的边数.
5.如果一个多边形的内角和与外角和之比是13:2,求这个多边形的边数.
6.如图,D是△ABC的边BC上一点,∠B=∠BAD,
∠C=∠ADC , ∠DAC=40?. 求:∠B的度数
A
B
C
D
40 ?
A
B
C
D
谢谢
祝好!
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
