北师大版 数学九年级上册 1.2矩形的性质与判定(1)课件 (共29张PPT)
文档属性
| 名称 | 北师大版 数学九年级上册 1.2矩形的性质与判定(1)课件 (共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-23 07:04:31 | ||
图片预览






文档简介
(共29张PPT)
1.2矩形的性质与判定(1)
第一章
教学目标
理解矩形的概念,了解它与平行四边形之间的关系;
01
02
经历矩形性质定理的探索与证明过程,进一步发展合情推理能力;探索并掌握直角三角形的性质定理;
03
体会探索与证明过程中所蕴含的抽象、推理等数学思想.
下面几幅图片中都含有一些平行四边形,观察这些平行四边形,你能发现它们有什么样的共同特征?
一、欣赏观察
有一个角是直角.
一、欣赏观察
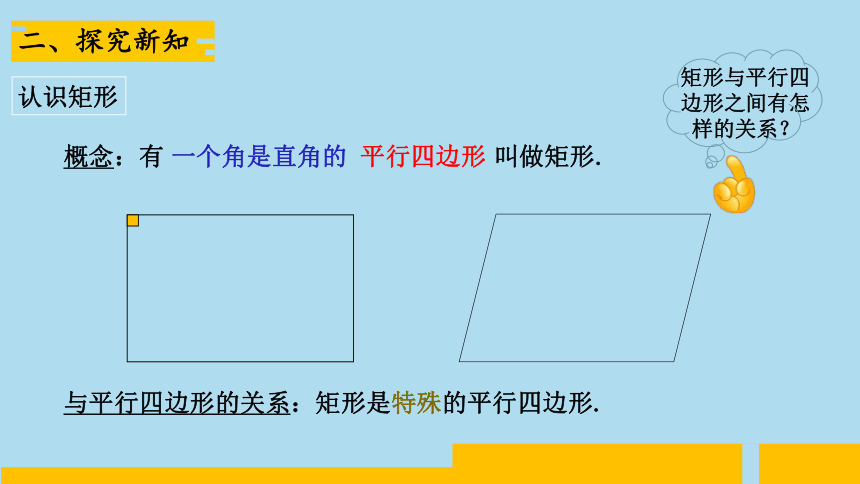
概念:有 叫做矩形.
认识矩形
与平行四边形的关系:矩形是特殊的平行四边形.
一个角是直角的
平行四边形
二、探究新知
矩形与平行四边形之间有怎样的关系?
二、探究新知
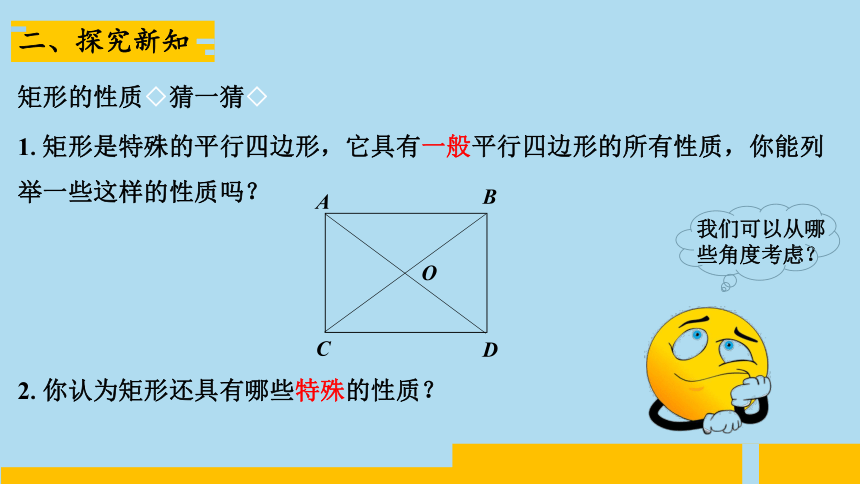
矩形的性质◇猜一猜◇
1.矩形是特殊的平行四边形,它具有一般平行四边形的所有性质,你能列举一些这样的性质吗?
2.你认为矩形还具有哪些特殊的性质?
我们可以从哪些角度考虑?
A
D
B
C
O
二、探究新知
矩形的性质◇做一做◇
用矩形纸片折一折,回答下列问题:
1.矩形是轴对称图形吗?如果是,它有几条对称轴?
矩形是轴对称图形.
二、探究新知
矩形的性质◇猜一猜◇
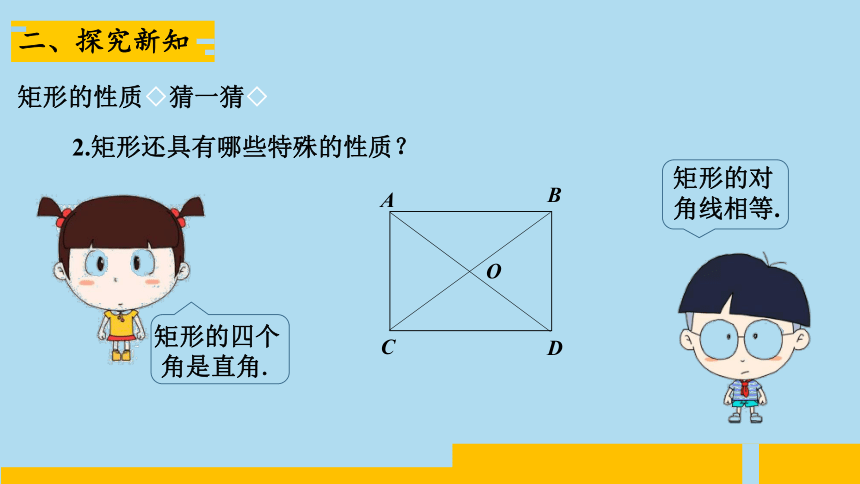
2.矩形还具有哪些特殊的性质?
A
D
B
C
O
矩形的四个角是直角.
矩形的对角线相等.
二、探究新知
矩形的性质◇证一证◇
已知:如图1-8,四边形ABCD是矩形,∠ABC=90°,对角线AC与BD相交
于点O.
(1)矩形的四个角是直角;(2)矩形的对角线相等.
证明:(1)∵四边形ABCD是矩形,
∴∠ABC=∠ADC,∠BCD=∠DAB(矩形的对角相等),
AB∥DC(矩形的对边平行).
求证:(1)∠ABC=∠BCD=∠CDA=∠DAB=90°;
图1-8
A
D
B
C
O
二、探究新知
矩形的性质◇证一证◇
证明:(1)∵四边形ABCD是矩形,
∴∠ABC=∠ADC,∠BCD=∠DAB(矩形的对角相等),
AB∥DC(矩形的对边平行).
图1-8
A
D
B
C
O
∴∠ABC+∠BCD=180°.
又∵∠ABC=90°,
∴∠BCD=90°.
∴∠ABC=∠BCD=∠CDA=∠DAB=90°.
二、探究新知
证明:(2)∵四边形ABCD是矩形,
∴AB=CD(矩形的对边相等).
求证:(2)AC=BD.
矩形的性质◇证一证◇
(1)矩形的四个角是直角;(2)矩形的对角线相等.
已知:如图1-8,四边形ABCD是矩形,∠ABC=90°,对角线AC与BD相交
于点O.
图1-8
A
D
B
C
O
二、探究新知
证明:(2)∵四边形ABCD是矩形,
∴AB=CD(矩形的对边相等).
求证:(2)AC=BD.
矩形的性质◇证一证◇
图1-8
A
D
B
C
O
在△ABC与△BCD中,
AB=CD,∠ABC=∠BCD,BC=BC,
∴△ABC≌△DCB.
∴AC=BD.
二、探究新知
矩形的性质◇结论◇
定理:矩形的四个角是直角;
定理:矩形的对角线相等.
∵四边形ABCD是矩形,
∴∠ABC=∠BCD=∠CDA=∠DAB=90°(矩形的四个角是直角).
AC=BD(矩形的对角线相等).
文字语言:
符号语言:
A
D
B
C
O
图1-8
三、深入探究
如图1-9,矩形ABCD的对角线AC与BD相交于点E,那么BE是Rt△ABC中一条怎样的线段?它与AC有什么大小关系?由此你能得到怎样的结论?
A
D
B
C
E
图1-9
直角三角形斜边上的中线 等于 斜边的一半.
Rt△ABC斜边上的中线
斜边AC的一半
你能进行证明吗?
三、深入探究
直角三角形斜边上的中线等于斜边的一半.
证明:延长BE到D,使BE=ED,连接AD,CD.
已知:如图,在Rt△ABC中,∠ABC=90°,BE是AC上的中线.
A
B
C
E
D
求证:
在四边形ABCD中,
∵AE=CE,BE=DE,
∴四边形ABCD是平行四边形.
三、深入探究
证明:延长BE到D,使BE=ED,连接AD,CD.
在四边形ABCD中,
∵AE=CE,BE=DE,
∴四边形ABCD是平行四边形.
A
B
C
E
D
∴AC=BD(矩形的对角线相等).
∴
∵∠ABC=90°,
∴四边形ABCD是矩形(矩形的定义).
三、深入探究
A
B
C
E
定理:直角三角形斜边上的中线等于斜边的一半.
文字语言:
符号语言:
◇直角三角形的性质◇
在Rt△ABC,AE=EC.
∴ (直角三角形斜边上的中线等于斜边的一半).
解:∵四边形ABCD是矩形,
∴∠DAB=90?(矩形的四个角都是直角),
AC=BD(矩形的对角线相等),
OA=OC= AC,OB=OD= BD(矩形的对角线互相平分),
∴OA=OD.
∵∠AOD=120?,
∴∠ODA=∠OAD=
∴BD=2AB=2×2.5=5.
四、典例分析
例1.如图1-10,在矩形ABCD中,两条对角线相交于点O,∠AOD=120?,AB=2.5,求这个矩形对角线的长.
A
D
B
C
O
图1-10
你还有其他方法吗?
四、典例分析
例1.如图1-10,在矩形ABCD中,两条对角线相交于点O,∠AOD=120?,AB=2.5,求这个矩形对角线的长.
A
D
B
C
O
图1-10
解:∵四边形ABCD是矩形,
∴AC=BD(矩形的对角线相等),
OA=OC= AC,OB=OD= BD(矩形的对角线互相平分),
∴OA=OB.
∵∠AOD=120?,
∴∠AOB=60?.
∴△AOB是等边三角形.
∴BD=2OB=2AB=2×2.5=5.
四、典例分析
A
D
B
C
O
图1-10
A
D
B
C
O
图1-10
转
化
五、随堂练习
1.一个矩形的对角线长为6,对角线与一边的夹角是45?,求这个矩形的各边长.
A
D
B
C
解:如图所示:∵四边形ABCD是矩形,
∴AB=CD, BC=AD, AC=BD=6,
∠BAD=90?(矩形的四个角是直角),
∵∠ABD=45?,
∴△ABD是等腰直角三角形,
∴AB=AD=
∴AB=BC=CD=AD
五、随堂练习
2.一个矩形的两条对角线的一个夹角为60?,对角线长15,求这个矩形较短边的长.
A
D
B
C
O
解:如图,∵四边形ABCD是矩形,
∴AC=BD=15(矩形的对角线相等),
OA=OC= AC, OB=OD= BD(矩形的对角线互相平分).
∴OA=OB=7.5.
∵∠AOB=60?,
∴△AOB是等边三角形,
∴AB=OA=7.5,即较短的边长为7.5.
五、随堂练习
3.如图,在Rt△ABC中,∠ACB=90?,D为AB中点,AE∥CD,CE∥AB.试判断四边形ADCE的形状,并证明你的结论.
解:四边形ADCE为菱形.
∵AE∥CD, CE∥AB,
∴四边形ADCE是平行四边形,
∵∠ACB=90?,D为AB的中点,
∴CD= AB(直角三角形斜边上的中线等于斜边的一半),
∴CD=AD
∴四边形ADCE为菱形.
五、随堂练习
4.证明:如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.
证明:∵CD是AB上的中线,
∴
∵
∴AD=BD=CD.
∴∠1=∠A,∠2=∠B.
已知:如图,在△ABC中,CD是AB上的中线,
求证:△ABC是直角三角形.
A
B
C
D
1
2
五、随堂练习
证明:∵CD是AB上的中线,
∴
∵
∴AD=BD=CD.
∴∠1=∠A,∠2=∠B.
A
B
C
D
1
2
∵∠1+∠A+∠2+∠B=180°.
∴2∠1+2∠2=180°.
∴∠ACB=∠1+∠2=90°
∴△ABC是直角三角形.
得到两个等腰三角形.
五、随堂练习
三角形一边上的中线等于这边的一半.
这个三角形是直角三角形.
斜边上的中线等于斜边的一半.
这个三角形是直角三角形.
◇直角三角形◇
性质
判定
六、课堂小结
矩形具有对称性;
性质:矩形的四个角是直角;
矩形的对角线相等.
概念:有一个角是直角的平行四边
形叫做矩形.
概念
性质
判定
应用
七、作业布置
完成练习册上习题.
同学们,再见!
1.2矩形的性质与判定(1)
第一章
教学目标
理解矩形的概念,了解它与平行四边形之间的关系;
01
02
经历矩形性质定理的探索与证明过程,进一步发展合情推理能力;探索并掌握直角三角形的性质定理;
03
体会探索与证明过程中所蕴含的抽象、推理等数学思想.
下面几幅图片中都含有一些平行四边形,观察这些平行四边形,你能发现它们有什么样的共同特征?
一、欣赏观察
有一个角是直角.
一、欣赏观察
概念:有 叫做矩形.
认识矩形
与平行四边形的关系:矩形是特殊的平行四边形.
一个角是直角的
平行四边形
二、探究新知
矩形与平行四边形之间有怎样的关系?
二、探究新知
矩形的性质◇猜一猜◇
1.矩形是特殊的平行四边形,它具有一般平行四边形的所有性质,你能列举一些这样的性质吗?
2.你认为矩形还具有哪些特殊的性质?
我们可以从哪些角度考虑?
A
D
B
C
O
二、探究新知
矩形的性质◇做一做◇
用矩形纸片折一折,回答下列问题:
1.矩形是轴对称图形吗?如果是,它有几条对称轴?
矩形是轴对称图形.
二、探究新知
矩形的性质◇猜一猜◇
2.矩形还具有哪些特殊的性质?
A
D
B
C
O
矩形的四个角是直角.
矩形的对角线相等.
二、探究新知
矩形的性质◇证一证◇
已知:如图1-8,四边形ABCD是矩形,∠ABC=90°,对角线AC与BD相交
于点O.
(1)矩形的四个角是直角;(2)矩形的对角线相等.
证明:(1)∵四边形ABCD是矩形,
∴∠ABC=∠ADC,∠BCD=∠DAB(矩形的对角相等),
AB∥DC(矩形的对边平行).
求证:(1)∠ABC=∠BCD=∠CDA=∠DAB=90°;
图1-8
A
D
B
C
O
二、探究新知
矩形的性质◇证一证◇
证明:(1)∵四边形ABCD是矩形,
∴∠ABC=∠ADC,∠BCD=∠DAB(矩形的对角相等),
AB∥DC(矩形的对边平行).
图1-8
A
D
B
C
O
∴∠ABC+∠BCD=180°.
又∵∠ABC=90°,
∴∠BCD=90°.
∴∠ABC=∠BCD=∠CDA=∠DAB=90°.
二、探究新知
证明:(2)∵四边形ABCD是矩形,
∴AB=CD(矩形的对边相等).
求证:(2)AC=BD.
矩形的性质◇证一证◇
(1)矩形的四个角是直角;(2)矩形的对角线相等.
已知:如图1-8,四边形ABCD是矩形,∠ABC=90°,对角线AC与BD相交
于点O.
图1-8
A
D
B
C
O
二、探究新知
证明:(2)∵四边形ABCD是矩形,
∴AB=CD(矩形的对边相等).
求证:(2)AC=BD.
矩形的性质◇证一证◇
图1-8
A
D
B
C
O
在△ABC与△BCD中,
AB=CD,∠ABC=∠BCD,BC=BC,
∴△ABC≌△DCB.
∴AC=BD.
二、探究新知
矩形的性质◇结论◇
定理:矩形的四个角是直角;
定理:矩形的对角线相等.
∵四边形ABCD是矩形,
∴∠ABC=∠BCD=∠CDA=∠DAB=90°(矩形的四个角是直角).
AC=BD(矩形的对角线相等).
文字语言:
符号语言:
A
D
B
C
O
图1-8
三、深入探究
如图1-9,矩形ABCD的对角线AC与BD相交于点E,那么BE是Rt△ABC中一条怎样的线段?它与AC有什么大小关系?由此你能得到怎样的结论?
A
D
B
C
E
图1-9
直角三角形斜边上的中线 等于 斜边的一半.
Rt△ABC斜边上的中线
斜边AC的一半
你能进行证明吗?
三、深入探究
直角三角形斜边上的中线等于斜边的一半.
证明:延长BE到D,使BE=ED,连接AD,CD.
已知:如图,在Rt△ABC中,∠ABC=90°,BE是AC上的中线.
A
B
C
E
D
求证:
在四边形ABCD中,
∵AE=CE,BE=DE,
∴四边形ABCD是平行四边形.
三、深入探究
证明:延长BE到D,使BE=ED,连接AD,CD.
在四边形ABCD中,
∵AE=CE,BE=DE,
∴四边形ABCD是平行四边形.
A
B
C
E
D
∴AC=BD(矩形的对角线相等).
∴
∵∠ABC=90°,
∴四边形ABCD是矩形(矩形的定义).
三、深入探究
A
B
C
E
定理:直角三角形斜边上的中线等于斜边的一半.
文字语言:
符号语言:
◇直角三角形的性质◇
在Rt△ABC,AE=EC.
∴ (直角三角形斜边上的中线等于斜边的一半).
解:∵四边形ABCD是矩形,
∴∠DAB=90?(矩形的四个角都是直角),
AC=BD(矩形的对角线相等),
OA=OC= AC,OB=OD= BD(矩形的对角线互相平分),
∴OA=OD.
∵∠AOD=120?,
∴∠ODA=∠OAD=
∴BD=2AB=2×2.5=5.
四、典例分析
例1.如图1-10,在矩形ABCD中,两条对角线相交于点O,∠AOD=120?,AB=2.5,求这个矩形对角线的长.
A
D
B
C
O
图1-10
你还有其他方法吗?
四、典例分析
例1.如图1-10,在矩形ABCD中,两条对角线相交于点O,∠AOD=120?,AB=2.5,求这个矩形对角线的长.
A
D
B
C
O
图1-10
解:∵四边形ABCD是矩形,
∴AC=BD(矩形的对角线相等),
OA=OC= AC,OB=OD= BD(矩形的对角线互相平分),
∴OA=OB.
∵∠AOD=120?,
∴∠AOB=60?.
∴△AOB是等边三角形.
∴BD=2OB=2AB=2×2.5=5.
四、典例分析
A
D
B
C
O
图1-10
A
D
B
C
O
图1-10
转
化
五、随堂练习
1.一个矩形的对角线长为6,对角线与一边的夹角是45?,求这个矩形的各边长.
A
D
B
C
解:如图所示:∵四边形ABCD是矩形,
∴AB=CD, BC=AD, AC=BD=6,
∠BAD=90?(矩形的四个角是直角),
∵∠ABD=45?,
∴△ABD是等腰直角三角形,
∴AB=AD=
∴AB=BC=CD=AD
五、随堂练习
2.一个矩形的两条对角线的一个夹角为60?,对角线长15,求这个矩形较短边的长.
A
D
B
C
O
解:如图,∵四边形ABCD是矩形,
∴AC=BD=15(矩形的对角线相等),
OA=OC= AC, OB=OD= BD(矩形的对角线互相平分).
∴OA=OB=7.5.
∵∠AOB=60?,
∴△AOB是等边三角形,
∴AB=OA=7.5,即较短的边长为7.5.
五、随堂练习
3.如图,在Rt△ABC中,∠ACB=90?,D为AB中点,AE∥CD,CE∥AB.试判断四边形ADCE的形状,并证明你的结论.
解:四边形ADCE为菱形.
∵AE∥CD, CE∥AB,
∴四边形ADCE是平行四边形,
∵∠ACB=90?,D为AB的中点,
∴CD= AB(直角三角形斜边上的中线等于斜边的一半),
∴CD=AD
∴四边形ADCE为菱形.
五、随堂练习
4.证明:如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.
证明:∵CD是AB上的中线,
∴
∵
∴AD=BD=CD.
∴∠1=∠A,∠2=∠B.
已知:如图,在△ABC中,CD是AB上的中线,
求证:△ABC是直角三角形.
A
B
C
D
1
2
五、随堂练习
证明:∵CD是AB上的中线,
∴
∵
∴AD=BD=CD.
∴∠1=∠A,∠2=∠B.
A
B
C
D
1
2
∵∠1+∠A+∠2+∠B=180°.
∴2∠1+2∠2=180°.
∴∠ACB=∠1+∠2=90°
∴△ABC是直角三角形.
得到两个等腰三角形.
五、随堂练习
三角形一边上的中线等于这边的一半.
这个三角形是直角三角形.
斜边上的中线等于斜边的一半.
这个三角形是直角三角形.
◇直角三角形◇
性质
判定
六、课堂小结
矩形具有对称性;
性质:矩形的四个角是直角;
矩形的对角线相等.
概念:有一个角是直角的平行四边
形叫做矩形.
概念
性质
判定
应用
七、作业布置
完成练习册上习题.
同学们,再见!
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
