2019-2020学年第二学期湘教版 八年级数学下册第2章四边形同步优化训练( 答案不全)
文档属性
| 名称 | 2019-2020学年第二学期湘教版 八年级数学下册第2章四边形同步优化训练( 答案不全) |  | |
| 格式 | zip | ||
| 文件大小 | 326.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-23 13:12:29 | ||
图片预览


文档简介
湘教版2019-2020年第二学期八年级数学四边形同步优化训练
一、单选题
1.如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是( ??)
A.6??????????? B.7??????????? C.8???????????? D.9
【答案】C
2.下列命题中,假命题是( )
A.顺次联结任意四边形四边中点所得的四边形是平行四边形
B.顺次联结对角线相等的四边形四边中点所得的四边形是菱形
C.顺次联结对角线互相垂直的四边形四边中点所得的四边形是矩形
D.顺次联结两组邻边互相垂直的四边形四边中点所得的四边形是矩形
【答案】D
3.如果一个多边形的内角和是外角和的5倍,那么这个多边形的边数是( )
A.10 B.11 C.12 D.13
【答案】C
4.如图,在中,将沿AC折叠后,点D恰好落在DC的延长线上的点E处.若,,则的周长为( )
A.12 B.15 C.18 D.21
【答案】C
5.如图,在Rt△ABC中,∠BAC=90°,AB=5,AC=12,P为边BC上一动点(P不与B、C重合),PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的取值范围是( )
A.≤AM<6 B.5≤AM<12
C.≤AM<12 D.≤AM<6
【答案】A
6.如图,由两个长为8,宽为4的全等矩形叠合而得到四边形ABCD,则四边形ABCD面积的最大值是( )
A.15 B.16 C.19 D.20
【答案】D
7.如图,在正方形ABCD外侧,作等边三角形ADE,AC、BE相交于点F,则∠CFE为()
A.150° B.145° C.135° D.120°
【答案】D
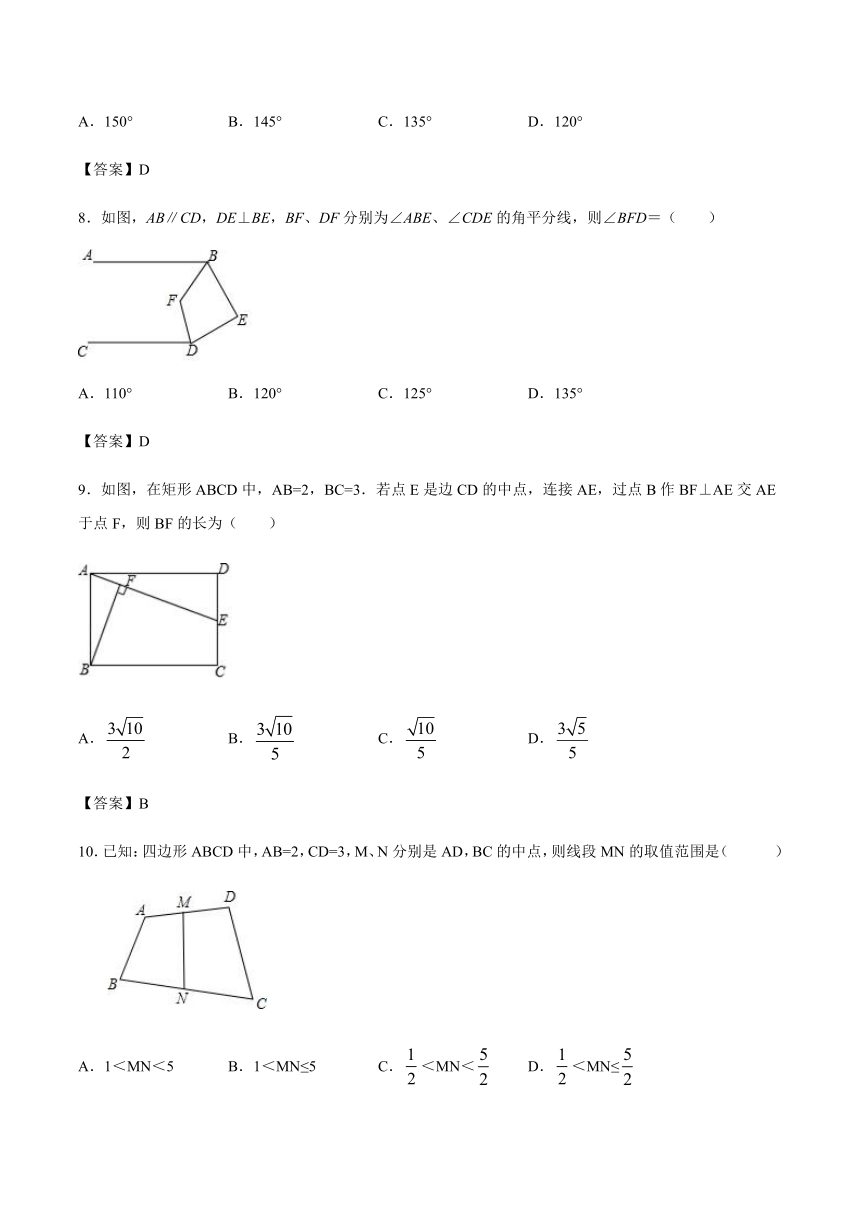
8.如图,AB∥CD,DE⊥BE,BF、DF分别为∠ABE、∠CDE的角平分线,则∠BFD=( )
A.110° B.120° C.125° D.135°
【答案】D
9.如图,在矩形ABCD中,AB=2,BC=3.若点E是边CD的中点,连接AE,过点B作BF⊥AE交AE于点F,则BF的长为( )
A. B. C. D.
【答案】B
10.已知:四边形ABCD中,AB=2,CD=3,M、N分别是AD,BC的中点,则线段MN的取值范围是( )
A.1<MN<5 B.1<MN≤5 C.<MN< D.<MN≤
【答案】D
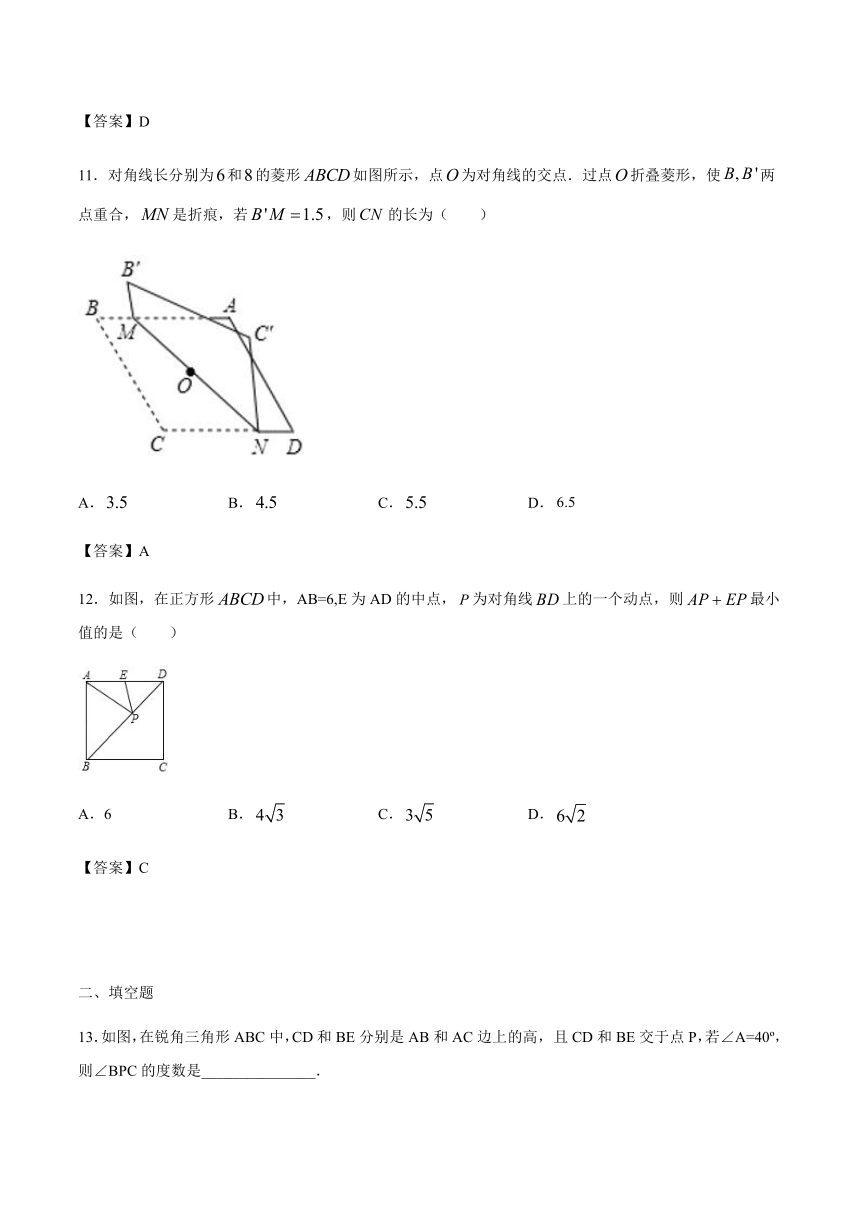
11.对角线长分别为和的菱形如图所示,点为对角线的交点.过点折叠菱形,使两点重合,是折痕,若,则的长为( )
A. B. C. D.
【答案】A
12.如图,在正方形中,AB=6,E为AD的中点,为对角线上的一个动点,则最小值的是( )
A.6 B. C. D.
【答案】C
二、填空题
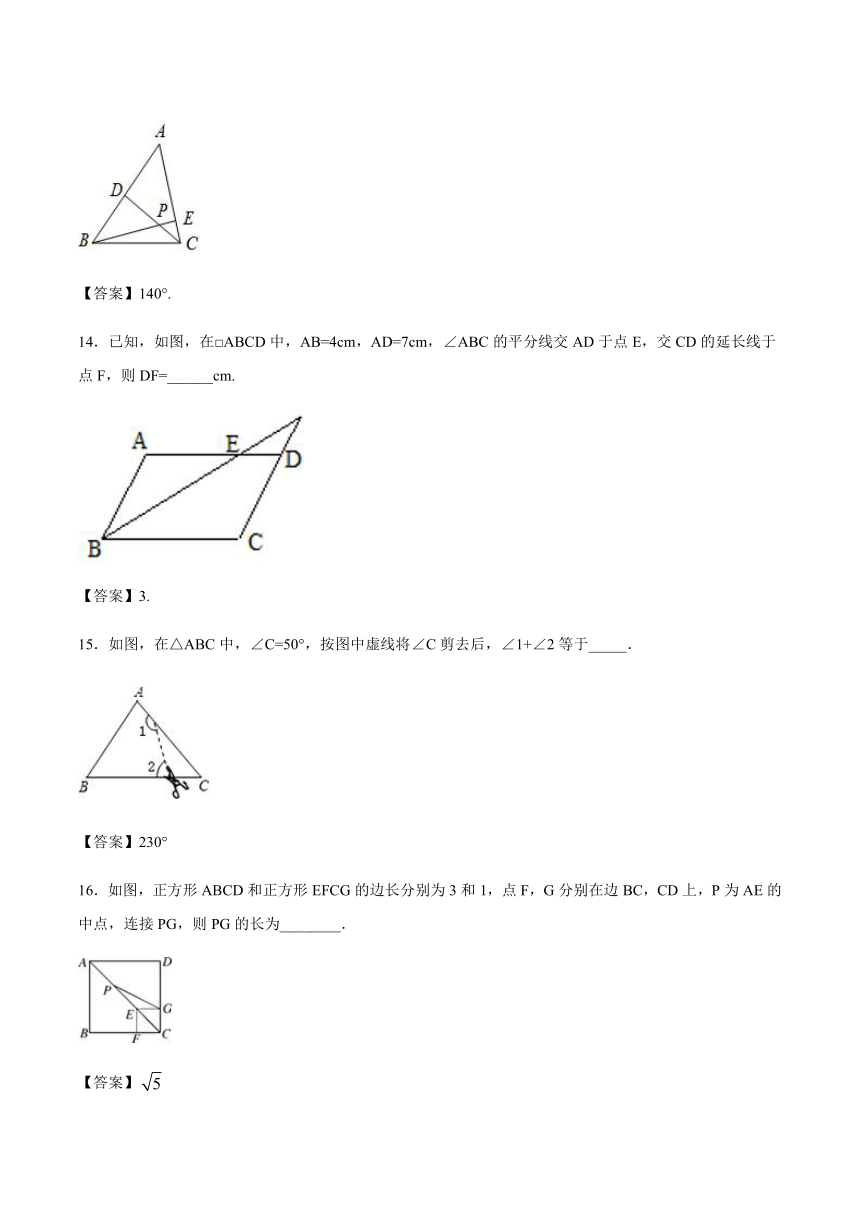
13.如图,在锐角三角形ABC中,CD和BE分别是AB和AC边上的高, 且CD和BE交于点P,若∠A=40?,则∠BPC的度数是_______________.
【答案】140°.
14.已知,如图,在□ABCD中,AB=4cm,AD=7cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF=______cm.
【答案】3.
15.如图,在△ABC中,∠C=50°,按图中虚线将∠C剪去后,∠1+∠2等于_____.
【答案】230°
16.如图,正方形ABCD和正方形EFCG的边长分别为3和1,点F,G分别在边BC,CD上,P为AE的中点,连接PG,则PG的长为________.
【答案】
17.如图,正方形ABCD的面积为1,则以相邻两边中点的连线EF为边的正方形EFGH的周长为________.
【答案】2
18.如图,在菱形中,是边上一点,且,有下列结论:①;②是等边三角形;③是等腰三角形;④,其中结论正确的有_______.
【答案】①②④
19.如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则S△ECF的值为____.
【答案】
20.如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为_____.
【答案】2 +2
三、解答题
21.如图,在矩形ABCD中,对角线AC,BD相交于点O,点O关于直线CD的对称点为E,连接DE,CE.
(1)求证:四边形ODEC为菱形;
(2)连接OE,若BC=2,求OE的长.
【答案】(1)略;(2)
22.如图,平行四边形ABCD中,对角线AC、BD相交于点O,若E、F是AC上两动点,分别从A、C两点以相同的速度1cm/s向C、A运动.
(1)四边形DEBF是平行四边形吗?请说明理由;
(2)若BD=12cm,AC=16cm,当运动时间t为何值时,四边形DEBF是矩形.
【答案】(1)是;(2)t=2或14.
23.如图,已知AC是矩形ABCD的对角线,AC的垂直平分线EF分别交BC、AD于点E和F,EF交AC于点O.
(1)求证:四边形AECF是菱形;(2)若AB=6,AD=8,求四边形AECF的周长.
【答案】(1)略(2)25
24.已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.
【答案】(1)证明略;(2)结论:四边形ACDF是矩形.
25.如图,已知四边形ABDE是平行四边形,C为边B D延长线上一点,连结AC、CE,使AB=AC.
(1)求证:△BAD≌△AEC;
(2)若∠B=30°,∠ADC=45°,BD=10,求平行四边形ABDE的面积.
【答案】(1)证明略;(2).
26.在?ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F
(1)在图1中证明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.
【答案】(1)略;(2)45°;(3)略.
27.如图,矩形ABCD中,AB=8,AD=10.
(1)E是CD上的点,将△ADE沿折痕AE折叠,使点D落在BC边上点F处.求DE的长;
(2)点P是线段CB延长线上的点,连接PA,若△PAF是等腰三角形,求PB的长;
(3)M是AD上的动点,在DC?上存在点N,使△MDN沿折痕MN折叠,点D落在BC边上点T处,请直接写出线段CT长度的最大值与最小值.
【答案】(1)5;(2)6或4或;(3)12.
28.操作体验:如图,在矩形ABCD中,点E、F分别在边AD、BC上,将矩形ABCD沿直线EF折叠,使点D恰好与点B重合,点C落在点C'处.点P为直线EF上一动点(不与E、F重合),过点P分别作直线BE、BF的垂线,垂足分别为点M和N,以PM、PN为邻边构造平行四边形PMQN.
(1)如图1,求证:BE=BF;
(2)特例感知:如图2,若DE=5,CF=3,当点P在线段EF上运动时,求平行四边形PMQN的周长;
(3)类比探究:如图3,当点P在线段EF的延长线上运动时,若DE=a,CF=b.请直接用含a、b的式子表示QM与QN之间的数量关系.(不要求写证明过程)
【答案】(1)证明略;(2)8;(3)QN﹣QM=.
一、单选题
1.如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是( ??)
A.6??????????? B.7??????????? C.8???????????? D.9
【答案】C
2.下列命题中,假命题是( )
A.顺次联结任意四边形四边中点所得的四边形是平行四边形
B.顺次联结对角线相等的四边形四边中点所得的四边形是菱形
C.顺次联结对角线互相垂直的四边形四边中点所得的四边形是矩形
D.顺次联结两组邻边互相垂直的四边形四边中点所得的四边形是矩形
【答案】D
3.如果一个多边形的内角和是外角和的5倍,那么这个多边形的边数是( )
A.10 B.11 C.12 D.13
【答案】C
4.如图,在中,将沿AC折叠后,点D恰好落在DC的延长线上的点E处.若,,则的周长为( )
A.12 B.15 C.18 D.21
【答案】C
5.如图,在Rt△ABC中,∠BAC=90°,AB=5,AC=12,P为边BC上一动点(P不与B、C重合),PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的取值范围是( )
A.≤AM<6 B.5≤AM<12
C.≤AM<12 D.≤AM<6
【答案】A
6.如图,由两个长为8,宽为4的全等矩形叠合而得到四边形ABCD,则四边形ABCD面积的最大值是( )
A.15 B.16 C.19 D.20
【答案】D
7.如图,在正方形ABCD外侧,作等边三角形ADE,AC、BE相交于点F,则∠CFE为()
A.150° B.145° C.135° D.120°
【答案】D
8.如图,AB∥CD,DE⊥BE,BF、DF分别为∠ABE、∠CDE的角平分线,则∠BFD=( )
A.110° B.120° C.125° D.135°
【答案】D
9.如图,在矩形ABCD中,AB=2,BC=3.若点E是边CD的中点,连接AE,过点B作BF⊥AE交AE于点F,则BF的长为( )
A. B. C. D.
【答案】B
10.已知:四边形ABCD中,AB=2,CD=3,M、N分别是AD,BC的中点,则线段MN的取值范围是( )
A.1<MN<5 B.1<MN≤5 C.<MN< D.<MN≤
【答案】D
11.对角线长分别为和的菱形如图所示,点为对角线的交点.过点折叠菱形,使两点重合,是折痕,若,则的长为( )
A. B. C. D.
【答案】A
12.如图,在正方形中,AB=6,E为AD的中点,为对角线上的一个动点,则最小值的是( )
A.6 B. C. D.
【答案】C
二、填空题
13.如图,在锐角三角形ABC中,CD和BE分别是AB和AC边上的高, 且CD和BE交于点P,若∠A=40?,则∠BPC的度数是_______________.
【答案】140°.
14.已知,如图,在□ABCD中,AB=4cm,AD=7cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF=______cm.
【答案】3.
15.如图,在△ABC中,∠C=50°,按图中虚线将∠C剪去后,∠1+∠2等于_____.
【答案】230°
16.如图,正方形ABCD和正方形EFCG的边长分别为3和1,点F,G分别在边BC,CD上,P为AE的中点,连接PG,则PG的长为________.
【答案】
17.如图,正方形ABCD的面积为1,则以相邻两边中点的连线EF为边的正方形EFGH的周长为________.
【答案】2
18.如图,在菱形中,是边上一点,且,有下列结论:①;②是等边三角形;③是等腰三角形;④,其中结论正确的有_______.
【答案】①②④
19.如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则S△ECF的值为____.
【答案】
20.如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为_____.
【答案】2 +2
三、解答题
21.如图,在矩形ABCD中,对角线AC,BD相交于点O,点O关于直线CD的对称点为E,连接DE,CE.
(1)求证:四边形ODEC为菱形;
(2)连接OE,若BC=2,求OE的长.
【答案】(1)略;(2)
22.如图,平行四边形ABCD中,对角线AC、BD相交于点O,若E、F是AC上两动点,分别从A、C两点以相同的速度1cm/s向C、A运动.
(1)四边形DEBF是平行四边形吗?请说明理由;
(2)若BD=12cm,AC=16cm,当运动时间t为何值时,四边形DEBF是矩形.
【答案】(1)是;(2)t=2或14.
23.如图,已知AC是矩形ABCD的对角线,AC的垂直平分线EF分别交BC、AD于点E和F,EF交AC于点O.
(1)求证:四边形AECF是菱形;(2)若AB=6,AD=8,求四边形AECF的周长.
【答案】(1)略(2)25
24.已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.
【答案】(1)证明略;(2)结论:四边形ACDF是矩形.
25.如图,已知四边形ABDE是平行四边形,C为边B D延长线上一点,连结AC、CE,使AB=AC.
(1)求证:△BAD≌△AEC;
(2)若∠B=30°,∠ADC=45°,BD=10,求平行四边形ABDE的面积.
【答案】(1)证明略;(2).
26.在?ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F
(1)在图1中证明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.
【答案】(1)略;(2)45°;(3)略.
27.如图,矩形ABCD中,AB=8,AD=10.
(1)E是CD上的点,将△ADE沿折痕AE折叠,使点D落在BC边上点F处.求DE的长;
(2)点P是线段CB延长线上的点,连接PA,若△PAF是等腰三角形,求PB的长;
(3)M是AD上的动点,在DC?上存在点N,使△MDN沿折痕MN折叠,点D落在BC边上点T处,请直接写出线段CT长度的最大值与最小值.
【答案】(1)5;(2)6或4或;(3)12.
28.操作体验:如图,在矩形ABCD中,点E、F分别在边AD、BC上,将矩形ABCD沿直线EF折叠,使点D恰好与点B重合,点C落在点C'处.点P为直线EF上一动点(不与E、F重合),过点P分别作直线BE、BF的垂线,垂足分别为点M和N,以PM、PN为邻边构造平行四边形PMQN.
(1)如图1,求证:BE=BF;
(2)特例感知:如图2,若DE=5,CF=3,当点P在线段EF上运动时,求平行四边形PMQN的周长;
(3)类比探究:如图3,当点P在线段EF的延长线上运动时,若DE=a,CF=b.请直接用含a、b的式子表示QM与QN之间的数量关系.(不要求写证明过程)
【答案】(1)证明略;(2)8;(3)QN﹣QM=.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
