五年级下册数学课件-6.5 总复习:图形与几何(立体图形的认识)▏沪教版 (共22张PPT)
文档属性
| 名称 | 五年级下册数学课件-6.5 总复习:图形与几何(立体图形的认识)▏沪教版 (共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 158.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-24 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
立体图形的复习
立体图形
长方体
正方体
圆锥体
圆柱体
立体图形
长方体
正方体
圆锥体
圆柱体
(特殊的长方体)
立体图形
长方体
正方体
圆锥体
圆柱体
都是平面围成的
有曲面
长方体和正方体的特点
6个面,至少有4个面是长方形。
6个面都是正方形。
12条棱,相对的棱长相等。
12条棱都相等。
8个顶点。
8个顶点。
形体名称 面 棱 顶点
长方体
正方体
圆柱体和圆锥体的特点
侧面是一个曲面,展开后可能是长方形或正方形……。
侧面也是一个曲面,展开后是一个扇形。
上、下两个相等的圆是上、下底面。
底面是一个圆。
形体名称 面
侧面 底面
圆柱体
圆锥体
练一练1:
1、填空
1、把圆柱的侧面沿高展开,一般可以得到 ( )形,这个长方形的长相当于( ),宽相当于( )。
2、用一根铁丝焊接成一个长10厘米、宽3厘米、高2厘米的长方体框架,至少需要铁丝( )厘米。
3、一个长方体最多可以有( )个面是正方形。
2、判断题
(1)长方体和正方体都有六个面,而且六个面都相等…( ) (2)圆锥体的高有一条;圆柱体的高有两条…………… ( ) (3)圆柱的侧面展开后是一个正方形,那么它的底面周长和高一定相等………………………( )
(4)正方体的棱长总和是48厘米,它的每条棱长是8厘米。
立体图形
长方体
正方体
圆锥体
圆柱体
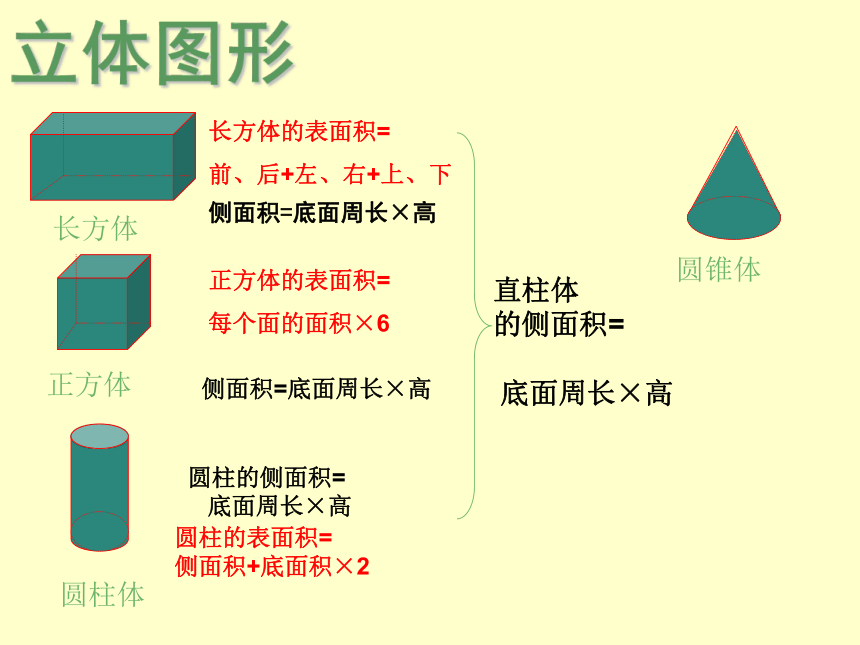
长方体的表面积=
前、后+左、右+上、下
正方体的表面积=
每个面的面积×6
圆柱的侧面积=
底面周长×高
圆柱的表面积=
侧面积+底面积×2
直柱体 的侧面积=
底面周长×高
侧面积=底面周长×高
侧面积=底面周长×高
练一练2:
1、填空
(1)做一个圆柱形铁皮罐头盒,求需要多少铁皮,是求它的( ),罐头盒周围贴商标纸, 求商标纸的面积是求它的( ) 。
(2)做一只圆柱形通风管要用多少铁皮,是求它的( )。
(3)下雨时,给打谷场上的圆锥形谷堆盖上塑料防雨布,所需防雨布的最小面积是指圆锥的( )。
表面积
侧面积
侧面积
侧面积
应用练习:
1、计算下列立体图形的表面积和侧面积;
10
5
4
5
5
5
2
10
单位:厘米
2、应用和计算 (1)用铁丝做一个长10厘米,宽5厘米,高4厘米的长方体柜架;至少需要多少长的铁丝?
在这个柜架外面糊一层纸,至少需要多少平方厘米的纸?
10
5
4
(2)把一根长3米,底面积直径2分米的圆柱形钢管截成3段,表面积增加了多少?
1
2
4
3
(3)一个圆柱形的水池,直径是20米,深2米 ①这个水池占地多少米?
③在池的侧面和池底贴磁砖,磁砖的面积是多少?
1.甲乙两人分别利用一张长20厘米, 宽15厘米的纸用两种不同的方法围成一个圆柱体(接头处不重叠),那么围成的圆柱( )。
A高一定相等 B侧面积一定相等C侧面积和高都相等
D侧面积和高都不相等
B
选择:
2.把一个棱长是2分米的正方体削成一个最大的圆柱体,它的侧面积是( )平方厘米。 A.6.28 B.12.56 C.18.84 D. 25.12
2
2
2
2×3.14×2
B
思考题.把一个圆柱形木材对半锯开,求半根木材的表面积(单位:厘米,得数保留整数。)
转化
实验、转化
推导体积计算公式
推导体积计算公式
立体图形体积计算
长方体
正方体
圆锥体
圆柱体
球
长方体的体积=
长×宽×高
正方体的体积=
棱长×棱长×棱长
圆柱的体积=底面积×高
圆锥体积=
×底面积×高
长方体、
正方体、
圆柱体的体积=
底面积×高
a
b
h
a
a
a
s
h
V=abh
V=sh
s
3
V=a
V=sh
V=sh
o
r
V= sh
V=sh
应用练习:
1、计算下列立体图形的表面积和体积;
10
5
4
5
5
5
2
10
单位:厘米
2、填空;
1、一个 正方体的底面周长是4分米,它的表面积是( ),体积是 ( )。
2、一个圆柱和圆锥的体积相等,底面积也相等。圆柱和圆锥的高的比是( )
把圆柱的侧面展开得一个长62.8厘米,宽31.4厘米的长方形。这个圆柱的体积可能是( )立方厘米,也可以是( )立方厘米。
思考题
立体图形的复习
立体图形
长方体
正方体
圆锥体
圆柱体
立体图形
长方体
正方体
圆锥体
圆柱体
(特殊的长方体)
立体图形
长方体
正方体
圆锥体
圆柱体
都是平面围成的
有曲面
长方体和正方体的特点
6个面,至少有4个面是长方形。
6个面都是正方形。
12条棱,相对的棱长相等。
12条棱都相等。
8个顶点。
8个顶点。
形体名称 面 棱 顶点
长方体
正方体
圆柱体和圆锥体的特点
侧面是一个曲面,展开后可能是长方形或正方形……。
侧面也是一个曲面,展开后是一个扇形。
上、下两个相等的圆是上、下底面。
底面是一个圆。
形体名称 面
侧面 底面
圆柱体
圆锥体
练一练1:
1、填空
1、把圆柱的侧面沿高展开,一般可以得到 ( )形,这个长方形的长相当于( ),宽相当于( )。
2、用一根铁丝焊接成一个长10厘米、宽3厘米、高2厘米的长方体框架,至少需要铁丝( )厘米。
3、一个长方体最多可以有( )个面是正方形。
2、判断题
(1)长方体和正方体都有六个面,而且六个面都相等…( ) (2)圆锥体的高有一条;圆柱体的高有两条…………… ( ) (3)圆柱的侧面展开后是一个正方形,那么它的底面周长和高一定相等………………………( )
(4)正方体的棱长总和是48厘米,它的每条棱长是8厘米。
立体图形
长方体
正方体
圆锥体
圆柱体
长方体的表面积=
前、后+左、右+上、下
正方体的表面积=
每个面的面积×6
圆柱的侧面积=
底面周长×高
圆柱的表面积=
侧面积+底面积×2
直柱体 的侧面积=
底面周长×高
侧面积=底面周长×高
侧面积=底面周长×高
练一练2:
1、填空
(1)做一个圆柱形铁皮罐头盒,求需要多少铁皮,是求它的( ),罐头盒周围贴商标纸, 求商标纸的面积是求它的( ) 。
(2)做一只圆柱形通风管要用多少铁皮,是求它的( )。
(3)下雨时,给打谷场上的圆锥形谷堆盖上塑料防雨布,所需防雨布的最小面积是指圆锥的( )。
表面积
侧面积
侧面积
侧面积
应用练习:
1、计算下列立体图形的表面积和侧面积;
10
5
4
5
5
5
2
10
单位:厘米
2、应用和计算 (1)用铁丝做一个长10厘米,宽5厘米,高4厘米的长方体柜架;至少需要多少长的铁丝?
在这个柜架外面糊一层纸,至少需要多少平方厘米的纸?
10
5
4
(2)把一根长3米,底面积直径2分米的圆柱形钢管截成3段,表面积增加了多少?
1
2
4
3
(3)一个圆柱形的水池,直径是20米,深2米 ①这个水池占地多少米?
③在池的侧面和池底贴磁砖,磁砖的面积是多少?
1.甲乙两人分别利用一张长20厘米, 宽15厘米的纸用两种不同的方法围成一个圆柱体(接头处不重叠),那么围成的圆柱( )。
A高一定相等 B侧面积一定相等C侧面积和高都相等
D侧面积和高都不相等
B
选择:
2.把一个棱长是2分米的正方体削成一个最大的圆柱体,它的侧面积是( )平方厘米。 A.6.28 B.12.56 C.18.84 D. 25.12
2
2
2
2×3.14×2
B
思考题.把一个圆柱形木材对半锯开,求半根木材的表面积(单位:厘米,得数保留整数。)
转化
实验、转化
推导体积计算公式
推导体积计算公式
立体图形体积计算
长方体
正方体
圆锥体
圆柱体
球
长方体的体积=
长×宽×高
正方体的体积=
棱长×棱长×棱长
圆柱的体积=底面积×高
圆锥体积=
×底面积×高
长方体、
正方体、
圆柱体的体积=
底面积×高
a
b
h
a
a
a
s
h
V=abh
V=sh
s
3
V=a
V=sh
V=sh
o
r
V= sh
V=sh
应用练习:
1、计算下列立体图形的表面积和体积;
10
5
4
5
5
5
2
10
单位:厘米
2、填空;
1、一个 正方体的底面周长是4分米,它的表面积是( ),体积是 ( )。
2、一个圆柱和圆锥的体积相等,底面积也相等。圆柱和圆锥的高的比是( )
把圆柱的侧面展开得一个长62.8厘米,宽31.4厘米的长方形。这个圆柱的体积可能是( )立方厘米,也可以是( )立方厘米。
思考题
