五年级下册数学课件-6.5 总复习:图形与几何(立体图形的认识)沪教版 (共18张PPT) (1)
文档属性
| 名称 | 五年级下册数学课件-6.5 总复习:图形与几何(立体图形的认识)沪教版 (共18张PPT) (1) |

|
|
| 格式 | zip | ||
| 文件大小 | 915.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-24 10:11:55 | ||
图片预览




文档简介
(共18张PPT)
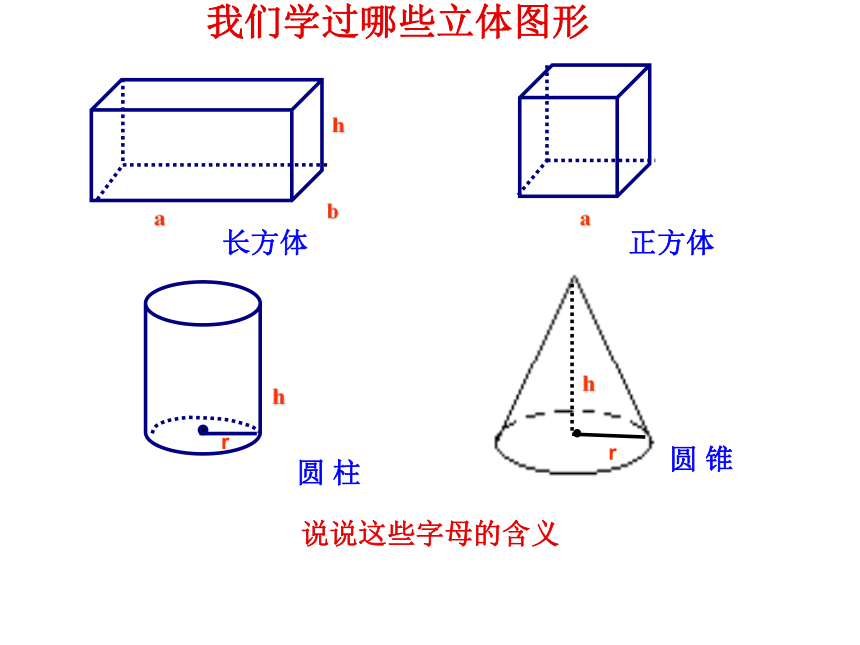
长方体
正方体
圆 锥
圆 柱
我们学过哪些立体图形
说说这些字母的含义
长方体
正方体
圆 锥
圆 柱
如果把这四种立体图形进行分类,你觉得应该怎么分?
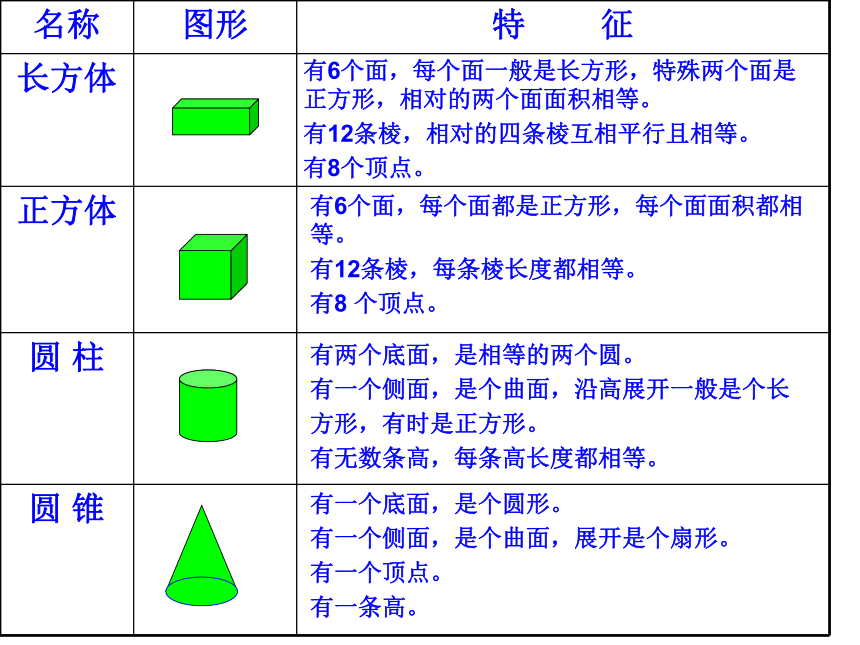
有6个面,每个面一般是长方形,特殊两个面是正方形,相对的两个面面积相等。
有12条棱,相对的四条棱互相平行且相等。
有8个顶点。
有6个面,每个面都是正方形,每个面面积都相等。
有12条棱,每条棱长度都相等。
有8 个顶点。
有两个底面,是相等的两个圆。
有一个侧面,是个曲面,沿高展开一般是个长
方形,有时是正方形。
有无数条高,每条高长度都相等。
有一个底面,是个圆形。
有一个侧面,是个曲面,展开是个扇形。
有一个顶点。
有一条高。
名称 图形 特 征
长方体
正方体
圆 柱
圆 锥
长方体和正方体有什么关系?
长方体 正方体
相同点 6个面,8个顶点,12条棱。
不
同
点 相对的四条棱的
长度相等 12条棱的长度
都相等
六个面都是长方形(有时相对的两个面都是正方形),每相对的两个面面积相等 有六个面都是正方形,并且每个面的面积都相等
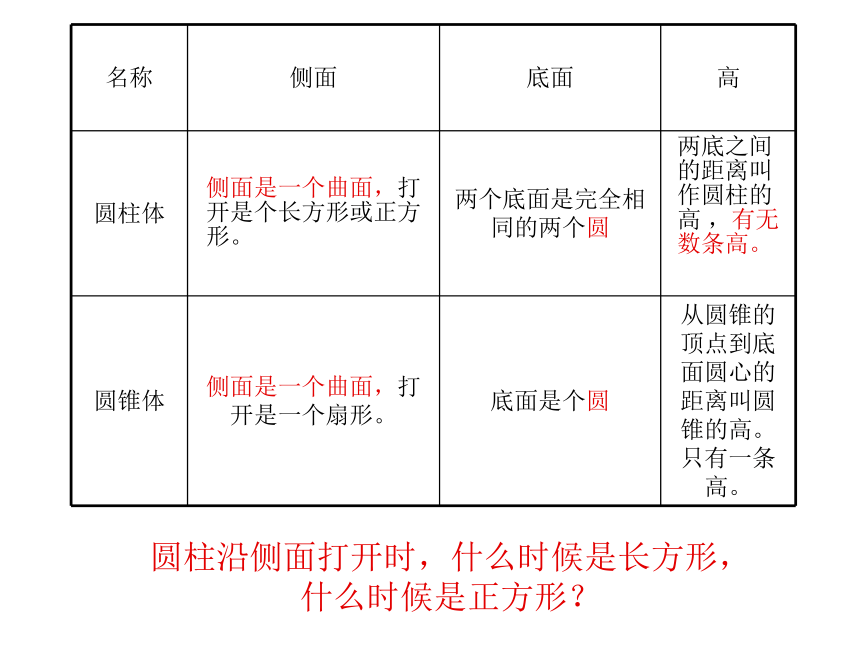
圆柱沿侧面打开时,什么时候是长方形,什么时候是正方形?
名称
侧面
底面 高
圆柱体 侧面是一个曲面,打开是个长方形或正方形。 两个底面是完全相同的两个圆 两底之间的距离叫作圆柱的高 ,有无数条高。
圆锥体 侧面是一个曲面,打开是一个扇形。 底面是个圆 从圆锥的顶点到底面圆心的距离叫圆锥的高。只有一条高。
长方体
正方体
圆 锥
圆 柱
分别从前面、上面、右面观察这四种立体图形,你分别看到了什么图形?
小学阶段我们不但学习了这些立体图形的特征,还学习这些立体图形的什么知识?
什么叫表面积?
物体所有面的总面积,叫作物体的表面积。
什么叫体积?
物体所占空间的大小叫作物体的体积。
长方体的表面积=
(长×宽+长×高×+宽×高)× 2
正方体的表面积=
棱长×棱长× 6
圆柱的表面积=
侧面积+底面积×2
圆柱的侧面积怎么算?为什么是底面周长×高?
长方体的体积=
长×宽×高
正方体的体积=
棱长×棱长×棱长
圆柱的体积=
底面积×高
圆锥的体积=
体积=底面积×高
回忆一下:圆柱的体积公式是什么?我们是如何推导的?
转化
怎么比较这三个立体图形的体积呢?谁会列式计算?
(1)5×2×3=30(立方厘米)
(2)3×3×3=27(立方厘米)
(3)3.14×2×2×3
=3.14×12
=37.68(立方厘米)
如果不计算体积结果,能比较出这三个立体图形体积的大小吗?
圆锥的体积公式是由什么推导出来的?
所选圆柱和圆锥要等底等高
实验
圆柱的体积是与它等底等高的圆锥体积的3倍
1、测测你的判断力
(1)体积单位比面积单位大。( )
(2)把一个圆柱削成一个最大的圆锥,削去部分的体积与圆锥的体积的比是2:1。( )
(3)把一个长方体铁块熔铸成一个圆柱体,形状虽然变了,但它们所占空间的大小没有变。( )
(4)一个圆柱的底面直径是4厘米,高是4 厘米,将这个圆柱的侧面展开后一定是一个正方形( )
×
√
√
×
2、填空。
(1)一个长方体的棱长总和是40厘米,其中长5厘米,宽3厘米,高是( )厘米。
(2)把两个棱长是3厘米的正方体木块拼成一个长方体,拼成的这个长方体的表面积是( ), 体积是( )。
(3)一个圆柱的底面积是1.5平方分米,那么与它体积和高都相等的圆锥的底面积应是( )平方分米。
(4)圆柱和圆锥等底等高,它们的体积之和是36立方厘米,那么圆柱的体积是( )立方厘米,圆锥的体积是( )立方厘米。
2
90平方厘米
54立方厘米
4.5
9
27
3、只列式,不计算
一个圆柱形的木桶,底面直径4分米,高50厘米。
①给木桶打两道铁箍,至少需要多长的铁丝?
②给木桶配上盖子,至少需要多少木板?
③在木桶外面涂油漆,油漆面的大小是多少平方厘米?
④ 这个木桶同能装多少水?
3.14 ×4 ×2
和同学们分享你的收获吧!
长方体
正方体
圆 锥
圆 柱
我们学过哪些立体图形
说说这些字母的含义
长方体
正方体
圆 锥
圆 柱
如果把这四种立体图形进行分类,你觉得应该怎么分?
有6个面,每个面一般是长方形,特殊两个面是正方形,相对的两个面面积相等。
有12条棱,相对的四条棱互相平行且相等。
有8个顶点。
有6个面,每个面都是正方形,每个面面积都相等。
有12条棱,每条棱长度都相等。
有8 个顶点。
有两个底面,是相等的两个圆。
有一个侧面,是个曲面,沿高展开一般是个长
方形,有时是正方形。
有无数条高,每条高长度都相等。
有一个底面,是个圆形。
有一个侧面,是个曲面,展开是个扇形。
有一个顶点。
有一条高。
名称 图形 特 征
长方体
正方体
圆 柱
圆 锥
长方体和正方体有什么关系?
长方体 正方体
相同点 6个面,8个顶点,12条棱。
不
同
点 相对的四条棱的
长度相等 12条棱的长度
都相等
六个面都是长方形(有时相对的两个面都是正方形),每相对的两个面面积相等 有六个面都是正方形,并且每个面的面积都相等
圆柱沿侧面打开时,什么时候是长方形,什么时候是正方形?
名称
侧面
底面 高
圆柱体 侧面是一个曲面,打开是个长方形或正方形。 两个底面是完全相同的两个圆 两底之间的距离叫作圆柱的高 ,有无数条高。
圆锥体 侧面是一个曲面,打开是一个扇形。 底面是个圆 从圆锥的顶点到底面圆心的距离叫圆锥的高。只有一条高。
长方体
正方体
圆 锥
圆 柱
分别从前面、上面、右面观察这四种立体图形,你分别看到了什么图形?
小学阶段我们不但学习了这些立体图形的特征,还学习这些立体图形的什么知识?
什么叫表面积?
物体所有面的总面积,叫作物体的表面积。
什么叫体积?
物体所占空间的大小叫作物体的体积。
长方体的表面积=
(长×宽+长×高×+宽×高)× 2
正方体的表面积=
棱长×棱长× 6
圆柱的表面积=
侧面积+底面积×2
圆柱的侧面积怎么算?为什么是底面周长×高?
长方体的体积=
长×宽×高
正方体的体积=
棱长×棱长×棱长
圆柱的体积=
底面积×高
圆锥的体积=
体积=底面积×高
回忆一下:圆柱的体积公式是什么?我们是如何推导的?
转化
怎么比较这三个立体图形的体积呢?谁会列式计算?
(1)5×2×3=30(立方厘米)
(2)3×3×3=27(立方厘米)
(3)3.14×2×2×3
=3.14×12
=37.68(立方厘米)
如果不计算体积结果,能比较出这三个立体图形体积的大小吗?
圆锥的体积公式是由什么推导出来的?
所选圆柱和圆锥要等底等高
实验
圆柱的体积是与它等底等高的圆锥体积的3倍
1、测测你的判断力
(1)体积单位比面积单位大。( )
(2)把一个圆柱削成一个最大的圆锥,削去部分的体积与圆锥的体积的比是2:1。( )
(3)把一个长方体铁块熔铸成一个圆柱体,形状虽然变了,但它们所占空间的大小没有变。( )
(4)一个圆柱的底面直径是4厘米,高是4 厘米,将这个圆柱的侧面展开后一定是一个正方形( )
×
√
√
×
2、填空。
(1)一个长方体的棱长总和是40厘米,其中长5厘米,宽3厘米,高是( )厘米。
(2)把两个棱长是3厘米的正方体木块拼成一个长方体,拼成的这个长方体的表面积是( ), 体积是( )。
(3)一个圆柱的底面积是1.5平方分米,那么与它体积和高都相等的圆锥的底面积应是( )平方分米。
(4)圆柱和圆锥等底等高,它们的体积之和是36立方厘米,那么圆柱的体积是( )立方厘米,圆锥的体积是( )立方厘米。
2
90平方厘米
54立方厘米
4.5
9
27
3、只列式,不计算
一个圆柱形的木桶,底面直径4分米,高50厘米。
①给木桶打两道铁箍,至少需要多长的铁丝?
②给木桶配上盖子,至少需要多少木板?
③在木桶外面涂油漆,油漆面的大小是多少平方厘米?
④ 这个木桶同能装多少水?
3.14 ×4 ×2
和同学们分享你的收获吧!
