人教版七年级下册数学课件 6. 2 立方根的概念课件(共53张PPT)
文档属性
| 名称 | 人教版七年级下册数学课件 6. 2 立方根的概念课件(共53张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-24 00:00:00 | ||
图片预览











文档简介
(共53张PPT)
初一年级 数学
立方根的概念
知识回顾
1.平方根的定义
一般地,如果一个数的平方等于a ,那么这个数叫做 a 的平方根或二次方根.这就是说 ,如果 x?=a ,那么 x 叫做 a 的平方根.即 a 的平方根可以用符号“ ”表示.
2.开平方
求一个数a的平方根的运算,叫做开平方.
平方与开平方互为逆运算.根据这种关系可以求一个数的平方根.
知识回顾
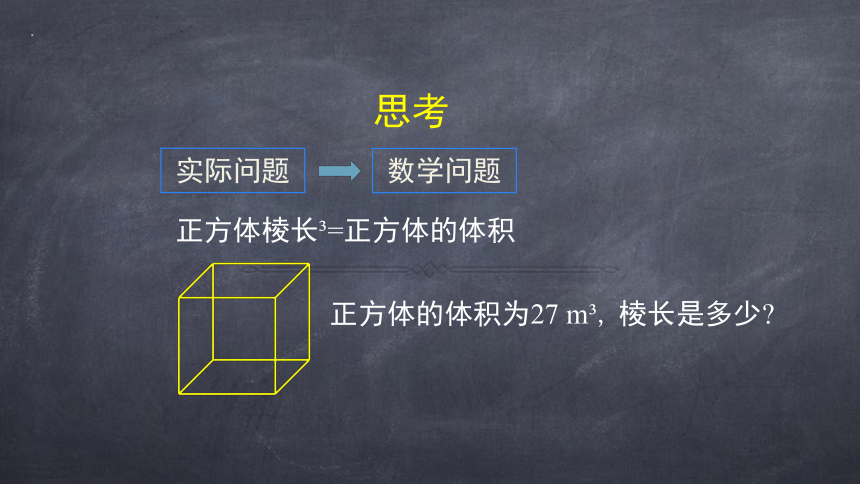
思考
要制作一种容积为 27 m? 的正方体形状的包装箱的棱长应该是多少呢?
思考
要制作一种容积为 27 m? 的正方体形状的包装箱的棱长应该是多少呢?
正方体棱长?=正方体的体积
思考
正方体棱长?=正方体的体积
正方体的体积为27 m?, 棱长是多少?
实际问题
数学问题
思考
正方体棱长? = 正方体的体积
正方体的体积为27 m?, 棱长是多少?
设正方体的棱长为 x m , 则
x? = 27
思考
正方体棱长? = 正方体的体积
设正方体的棱长为 x m , 则
x? = 27
已知幂和指数,求底数.
正方体的体积为27 m?, 棱长是多少?
思考
正方体棱长? = 正方体的体积
设正方体的棱长为 x m , 则
x? = 27
因为 3? = 27, 所以 x = 3.因此棱长为3 m.
正方体的体积为27 m?, 棱长是多少?
正方体的体积/ m? 1 8 27 64
正方体的棱长/ m
思考
x? = a .
设正方体的棱长为 x m , 则
1
2
3
4
a (a>0)
?
立方根的定义
一般地,如果一个数的立方等于a,那么这个数叫做 a 的立方根或三次方根.这就是说,如果 x?=a , 那么 x 叫做 a 的立方根.用符号“ ”表示,读作“三次根号a”,其中a是被开方数,3是根指数.
立方根的定义
一般地,如果一个数的立方等于a,那么这个数叫做 a 的立方根或三次方根.这就是说,如果 x?=a , 那么 x 叫做 a 的立方根.用符号“ ”表示,读作“三次根号a”,其中a是被开方数,3是根指数.
根指数3不能省略.
立方根的定义
中的根指数3为什么不能省略?
算术平方根的符号 ,实质上省略了 中的根指数 2 .
因此 也可读作“二次根号 a ”.
立方根的定义
一般地,如果一个数的立方等于a,那么这个数叫做 a 的立方根或三次方根.这就是说,如果 x?=a , 那么 x 叫做 a 的立方根.用符号“ ”表示,读作“三次根号a”,其中a是被开方数,3是根指数.
例如, 2?=8 , 2叫做8的立方根.
符号表示为 .
正方体的体积/ m? 1 8 27 64
正方体的棱长/ m
思考
x? = a .
设正方体的棱长为 x m , 则
1
2
3
4
a (a>0)
因此棱长为 m.
定义 表示法
平方根 如果x2=a,那么x叫做a的平方根.
(a ≥ 0)
立方根 如果x?=a,那么x叫做a的立方根.
小结归纳
平方根与立方根定义对比
判断下列说法是否正确:
(1) 5是125的立方根;
典型例题
(3) 7是21的立方根;
(2) 是64的立方根;
(4) 0.1是0.01的立方根;
(5) 是 的立方根.
根据立方根的定义进行判断.
正确
错误
改正:4是64的立方根.
错误
错误
正确
改正:7是343的立方根.
改正:0.1是0.001的立方根.
求下列各数的立方根:
(1) 1000 ; (2) ; (3) 0.729; (4) .
典型例题
求下列各数的立方根:
(1) 1000 ; (2) ; (3) 0.729; (4) .
典型例题
分析: 根据立方根的定义求解各数立方根 .
求下列各数的立方根:
典型例题
解:(1) 因为10?=1000 ,
所以1000的立方根是10 ,
即 .
(1) 1000 ; (2) ; (3) 0.729; (4) .
求下列各数的立方根:
典型例题
解 :(2) 因为 ,所以 的立方根是 ,
即 .
(1) 1000 ; (2) ; (3) 0.729; (4) .
求下列各数的立方根:
典型例题
解 :(3) 因为 ,
所以0.729的立方根是0.9 ,
即 .
(1) 1000 ; (2) ; (3) 0.729; (4) .
求下列各数的立方根:
方法2 : (3) 由于 ,
只需求 的立方根即可.
典型例题
(1) 1000 ; (2) ; (3) 0.729; (4) .
求下列各数的立方根:
解 :(4) 因为 , ,所以 的
典型例题
立方根是 ,即 .
(1) 1000 ; (2) ; (3) 0.729; (4) .
求下列各数的立方根:
巩固练习
(1) 216 ; (2) ; (3) 0.343 .
求下列各数的立方根:
巩固练习
解: (1) 因为 6? = 216 ,
所以 216 的立方根是6 ,
即
(1) 216 ; (2) ; (3) 0.343 .
求下列各数的立方根:
巩固练习
解: (2) 因为 ,所以 的立方根是 ,
即
(1) 216 ; (2) ; (3) 0.343 .
求下列各数的立方根:
巩固练习
解: (3) 因为 ,所以 0.343的立方根是 0.7 ,
即
(1) 216 ; (2) ; (3) 0.343 .
开立方
求一个数的立方根的运算,叫做开立方.
-2
-1
0
1
2
-8
-1
0
1
8
-2
-1
0
1
2
-8
-1
0
1
8
立方
开立方
求一个数的立方根的运算,叫做开立方.
开立方与立方互为逆运算.
开立方
定义 表示方法
立方根 一般地,如果一个数的立方等于a,那么这个数叫做a的立方根或三次方根. 一个数a的立方根,用“ ”表示,读作“三次根号a”,其中a是被开方数,3是根指数.
开立方
求一个数的立方根的运算叫做开立方.
立方根与开立方
求下列各式的值:
(1) ; (2) ; (3) ; (4) .
典型例题
求下列各式的值:
(1) ; (2) ; (3) ; (4) .
典型例题
解: (1) 表示64的立方根 ,
因为4?=64 , 所以 =4 ;
求下列各式的值:
(1) ; (2) ; (3) ; (4) .
典型例题
解 : (2) 表示0.027的立方根 ,
因为 0.3?=0.027,所以 = 0.3 ;
求下列各式的值:
典型例题
(1) ; (2) ; (3) ; (4) .
解 : (3) 表示 的立方根的相反数 ,又 ,
则 ,所以 ;
求下列各式的值:
(1) ; (2) ; (3) ; (4) .
典型例题
解 : (4) 表示 的立方根 ,
因为 , 所以 .
求下列各式的值:
巩固练习
(1) ; (2) ; (3) .
求下列各式的值:
巩固练习
(1) ; (2) ; (3) .
解 : (1) 因为 , 所以 .
又因为 , 所以 .
求下列各式的值:
巩固练习
(1) ; (2) ; (3) .
解 : (2) 因为 , 所以 .
又因为 , 所以 .
求下列各式的值:
巩固练习
(1) ; (2) ; (3) .
解 : (3) 因为2?-35 = -27, 所以 .
又因为 , 所以 .
小结
求一个数的立方根的方法:
根据开立方与立方互为逆运算求一个数的立方根.
求下列各式中x的值:
典型例题
(1) ; (2) ; (3) .
求下列各式中x的值:
分析: 根据立方根的定义求 x 的值 .
典型例题
(1) ; (2) ; (3) .
求下列各式中x的值:
(1) ; (2) ; (3) .
解 : (1)
典型例题
.
.
.
求下列各式中x的值:
解: (2) .
.
典型例题
(1) ; (2) ; (3) .
求下列各式中x的值:
解: (3)
典型例题
(1) ; (2) ; (3) .
.
.
.
.
求下列各式中 x 的值:
巩固练习
(1) ; (2) .
求下列各式中 x 的值:
巩固练习
(1) ; (2) .
解 : (1) .
.
.
求下列各式中 x 的值:
巩固练习
(1) ; (2) .
解 : (2) . .
. .
.
课堂小结
(1)立方根的概念及符号表示 ;
(2)开立方
.
一般地,如果一个数的立方等于a,那么这个数叫做 a 的立方根或三次方根.这就是说,如果 x?=a , 那么 x 叫做 a 的立方根.用符号“ ”表示,读作“三次根号a”,其中a是被开方数,3是根指数.
课后作业
教材51页练习1 .
求下列各式的值:
(1) ; (2) ; (3) ; (4)
.
希望同学们能够进一步理解、掌握并能够灵活运用本节课所学的内容.也期待和同学们共同学习下一节,同学下次再见!
初一年级 数学
立方根的概念
知识回顾
1.平方根的定义
一般地,如果一个数的平方等于a ,那么这个数叫做 a 的平方根或二次方根.这就是说 ,如果 x?=a ,那么 x 叫做 a 的平方根.即 a 的平方根可以用符号“ ”表示.
2.开平方
求一个数a的平方根的运算,叫做开平方.
平方与开平方互为逆运算.根据这种关系可以求一个数的平方根.
知识回顾
思考
要制作一种容积为 27 m? 的正方体形状的包装箱的棱长应该是多少呢?
思考
要制作一种容积为 27 m? 的正方体形状的包装箱的棱长应该是多少呢?
正方体棱长?=正方体的体积
思考
正方体棱长?=正方体的体积
正方体的体积为27 m?, 棱长是多少?
实际问题
数学问题
思考
正方体棱长? = 正方体的体积
正方体的体积为27 m?, 棱长是多少?
设正方体的棱长为 x m , 则
x? = 27
思考
正方体棱长? = 正方体的体积
设正方体的棱长为 x m , 则
x? = 27
已知幂和指数,求底数.
正方体的体积为27 m?, 棱长是多少?
思考
正方体棱长? = 正方体的体积
设正方体的棱长为 x m , 则
x? = 27
因为 3? = 27, 所以 x = 3.因此棱长为3 m.
正方体的体积为27 m?, 棱长是多少?
正方体的体积/ m? 1 8 27 64
正方体的棱长/ m
思考
x? = a .
设正方体的棱长为 x m , 则
1
2
3
4
a (a>0)
?
立方根的定义
一般地,如果一个数的立方等于a,那么这个数叫做 a 的立方根或三次方根.这就是说,如果 x?=a , 那么 x 叫做 a 的立方根.用符号“ ”表示,读作“三次根号a”,其中a是被开方数,3是根指数.
立方根的定义
一般地,如果一个数的立方等于a,那么这个数叫做 a 的立方根或三次方根.这就是说,如果 x?=a , 那么 x 叫做 a 的立方根.用符号“ ”表示,读作“三次根号a”,其中a是被开方数,3是根指数.
根指数3不能省略.
立方根的定义
中的根指数3为什么不能省略?
算术平方根的符号 ,实质上省略了 中的根指数 2 .
因此 也可读作“二次根号 a ”.
立方根的定义
一般地,如果一个数的立方等于a,那么这个数叫做 a 的立方根或三次方根.这就是说,如果 x?=a , 那么 x 叫做 a 的立方根.用符号“ ”表示,读作“三次根号a”,其中a是被开方数,3是根指数.
例如, 2?=8 , 2叫做8的立方根.
符号表示为 .
正方体的体积/ m? 1 8 27 64
正方体的棱长/ m
思考
x? = a .
设正方体的棱长为 x m , 则
1
2
3
4
a (a>0)
因此棱长为 m.
定义 表示法
平方根 如果x2=a,那么x叫做a的平方根.
(a ≥ 0)
立方根 如果x?=a,那么x叫做a的立方根.
小结归纳
平方根与立方根定义对比
判断下列说法是否正确:
(1) 5是125的立方根;
典型例题
(3) 7是21的立方根;
(2) 是64的立方根;
(4) 0.1是0.01的立方根;
(5) 是 的立方根.
根据立方根的定义进行判断.
正确
错误
改正:4是64的立方根.
错误
错误
正确
改正:7是343的立方根.
改正:0.1是0.001的立方根.
求下列各数的立方根:
(1) 1000 ; (2) ; (3) 0.729; (4) .
典型例题
求下列各数的立方根:
(1) 1000 ; (2) ; (3) 0.729; (4) .
典型例题
分析: 根据立方根的定义求解各数立方根 .
求下列各数的立方根:
典型例题
解:(1) 因为10?=1000 ,
所以1000的立方根是10 ,
即 .
(1) 1000 ; (2) ; (3) 0.729; (4) .
求下列各数的立方根:
典型例题
解 :(2) 因为 ,所以 的立方根是 ,
即 .
(1) 1000 ; (2) ; (3) 0.729; (4) .
求下列各数的立方根:
典型例题
解 :(3) 因为 ,
所以0.729的立方根是0.9 ,
即 .
(1) 1000 ; (2) ; (3) 0.729; (4) .
求下列各数的立方根:
方法2 : (3) 由于 ,
只需求 的立方根即可.
典型例题
(1) 1000 ; (2) ; (3) 0.729; (4) .
求下列各数的立方根:
解 :(4) 因为 , ,所以 的
典型例题
立方根是 ,即 .
(1) 1000 ; (2) ; (3) 0.729; (4) .
求下列各数的立方根:
巩固练习
(1) 216 ; (2) ; (3) 0.343 .
求下列各数的立方根:
巩固练习
解: (1) 因为 6? = 216 ,
所以 216 的立方根是6 ,
即
(1) 216 ; (2) ; (3) 0.343 .
求下列各数的立方根:
巩固练习
解: (2) 因为 ,所以 的立方根是 ,
即
(1) 216 ; (2) ; (3) 0.343 .
求下列各数的立方根:
巩固练习
解: (3) 因为 ,所以 0.343的立方根是 0.7 ,
即
(1) 216 ; (2) ; (3) 0.343 .
开立方
求一个数的立方根的运算,叫做开立方.
-2
-1
0
1
2
-8
-1
0
1
8
-2
-1
0
1
2
-8
-1
0
1
8
立方
开立方
求一个数的立方根的运算,叫做开立方.
开立方与立方互为逆运算.
开立方
定义 表示方法
立方根 一般地,如果一个数的立方等于a,那么这个数叫做a的立方根或三次方根. 一个数a的立方根,用“ ”表示,读作“三次根号a”,其中a是被开方数,3是根指数.
开立方
求一个数的立方根的运算叫做开立方.
立方根与开立方
求下列各式的值:
(1) ; (2) ; (3) ; (4) .
典型例题
求下列各式的值:
(1) ; (2) ; (3) ; (4) .
典型例题
解: (1) 表示64的立方根 ,
因为4?=64 , 所以 =4 ;
求下列各式的值:
(1) ; (2) ; (3) ; (4) .
典型例题
解 : (2) 表示0.027的立方根 ,
因为 0.3?=0.027,所以 = 0.3 ;
求下列各式的值:
典型例题
(1) ; (2) ; (3) ; (4) .
解 : (3) 表示 的立方根的相反数 ,又 ,
则 ,所以 ;
求下列各式的值:
(1) ; (2) ; (3) ; (4) .
典型例题
解 : (4) 表示 的立方根 ,
因为 , 所以 .
求下列各式的值:
巩固练习
(1) ; (2) ; (3) .
求下列各式的值:
巩固练习
(1) ; (2) ; (3) .
解 : (1) 因为 , 所以 .
又因为 , 所以 .
求下列各式的值:
巩固练习
(1) ; (2) ; (3) .
解 : (2) 因为 , 所以 .
又因为 , 所以 .
求下列各式的值:
巩固练习
(1) ; (2) ; (3) .
解 : (3) 因为2?-35 = -27, 所以 .
又因为 , 所以 .
小结
求一个数的立方根的方法:
根据开立方与立方互为逆运算求一个数的立方根.
求下列各式中x的值:
典型例题
(1) ; (2) ; (3) .
求下列各式中x的值:
分析: 根据立方根的定义求 x 的值 .
典型例题
(1) ; (2) ; (3) .
求下列各式中x的值:
(1) ; (2) ; (3) .
解 : (1)
典型例题
.
.
.
求下列各式中x的值:
解: (2) .
.
典型例题
(1) ; (2) ; (3) .
求下列各式中x的值:
解: (3)
典型例题
(1) ; (2) ; (3) .
.
.
.
.
求下列各式中 x 的值:
巩固练习
(1) ; (2) .
求下列各式中 x 的值:
巩固练习
(1) ; (2) .
解 : (1) .
.
.
求下列各式中 x 的值:
巩固练习
(1) ; (2) .
解 : (2) . .
. .
.
课堂小结
(1)立方根的概念及符号表示 ;
(2)开立方
.
一般地,如果一个数的立方等于a,那么这个数叫做 a 的立方根或三次方根.这就是说,如果 x?=a , 那么 x 叫做 a 的立方根.用符号“ ”表示,读作“三次根号a”,其中a是被开方数,3是根指数.
课后作业
教材51页练习1 .
求下列各式的值:
(1) ; (2) ; (3) ; (4)
.
希望同学们能够进一步理解、掌握并能够灵活运用本节课所学的内容.也期待和同学们共同学习下一节,同学下次再见!
