10.2.2 平行线的判定(一)(要点测评+课后集训+答案)
文档属性
| 名称 | 10.2.2 平行线的判定(一)(要点测评+课后集训+答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-24 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
沪科版数学七年级下册同步课时训练
第10章 相交线、平行线与平移
10.2 平行线的判定
第2课时 平行线的判定(一)
要点测评 基础达标
要点1 同位角相等两直线平行
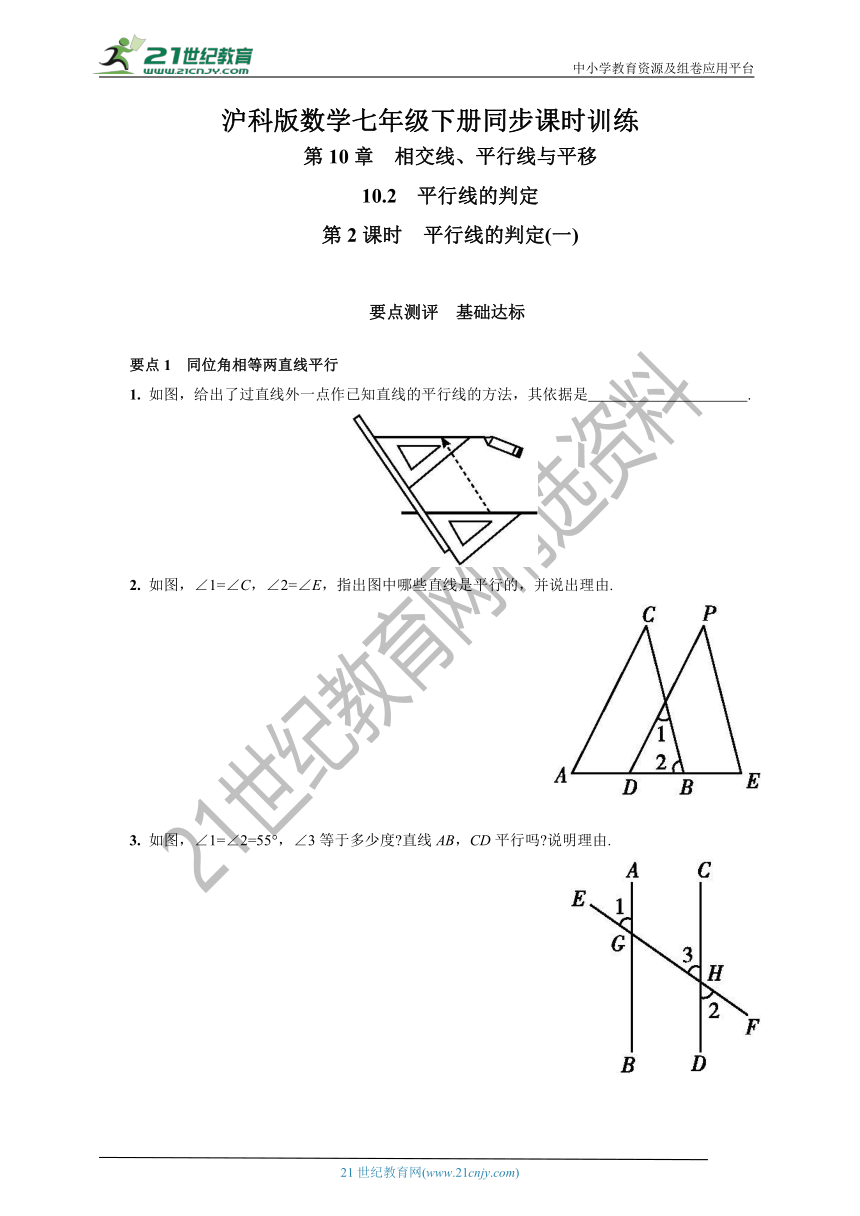
1. 如图,给出了过直线外一点作已知直线的平行线的方法,其依据是 .
2. 如图,∠1=∠C,∠2=∠E,指出图中哪些直线是平行的,并说出理由.
3. 如图,∠1=∠2=55°,∠3等于多少度?直线AB,CD平行吗?说明理由.
要点2 在同一平面内垂直于同一直线的两直线平行
4. 同一平面内的四条直线若满足a⊥b,b⊥c,c⊥d,则下列式子成立的是( )
A. a∥d B. b⊥d C. a⊥d D. b∥c
5. 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线 .?
图1 图2
(1)它的理由如下:(如图1)
因为b⊥a,c⊥a,所以∠1=∠2=90°,
所以b∥c( )?
(2)如图2是木工师傅使用角尺画平行线,有什么道理?
.?
课后集训 巩固提升
6. 如图,直线a,b被直线c所截,下列条件能判断a∥b的是( )
A. ∠1=∠2 B. ∠1=∠4
C. ∠3+∠4=180° D. ∠2=30°,∠4=35°
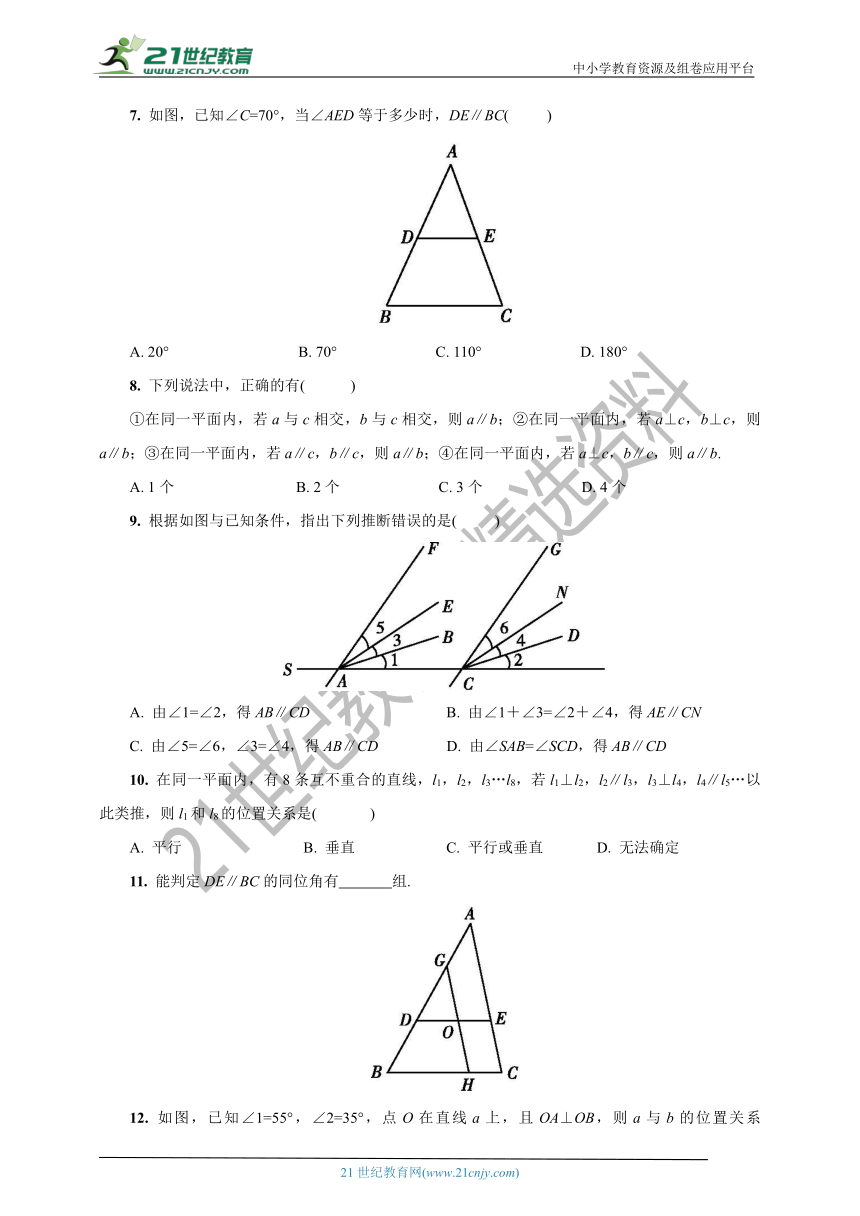
7. 如图,已知∠C=70°,当∠AED等于多少时,DE∥BC( )
A. 20° B. 70° C. 110° D. 180°
8. 下列说法中,正确的有( )
①在同一平面内,若a与c相交,b与c相交,则a∥b;②在同一平面内,若a⊥c,b⊥c,则a∥b;③在同一平面内,若a∥c,b∥c,则a∥b;④在同一平面内,若a⊥c,b∥c,则a∥b.
A. 1个 B. 2个 C. 3个 D. 4个
9. 根据如图与已知条件,指出下列推断错误的是( )
A. 由∠1=∠2,得AB∥CD B. 由∠1+∠3=∠2+∠4,得AE∥CN
C. 由∠5=∠6,∠3=∠4,得AB∥CD D. 由∠SAB=∠SCD,得AB∥CD
10. 在同一平面内,有8条互不重合的直线,l1,l2,l3…l8,若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5…以此类推,则l1和l8的位置关系是( )
A. 平行 B. 垂直 C. 平行或垂直 D. 无法确定
11. 能判定DE∥BC的同位角有 组.?
12. 如图,已知∠1=55°,∠2=35°,点O在直线a上,且OA⊥OB,则a与b的位置关系是 .?
13. 设a,b,l为平面内三条不同直线.①若a∥b,l⊥a,则l与b的位置关系是 ;②若l⊥a,l⊥b,则a与b的位置关系是 ;③若a∥b,l∥a,则l与b的位置关系是 .?
14. 我们已经掌握“在同一平面内,垂直于同一条直线的两条直线互相平行”这一判定两直线平行的方法.如图,已知直线AB和直线外一点C,请按照上述方法利用三角尺过点C画AB的平行线.(保留作图痕迹,不用写作法)
15. 如图,已知∠ABC=∠ACB,∠1=∠2,∠3=∠F,试判断EC与DF是否平行,并说明理由.
16. 学习了平行线后,小敏想出了过已知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如图(1)~(4)).从图中操作过程你知道小敏画平行线的依据吗?请把你的想法写出来.
参 考 答 案
1. 同位角相等,两直线平行
2. 解:AC∥DP,BC∥PE,理由是:因为∠1=∠C,所以AC∥DP(同位角相等,两直线平行),因为∠2=∠E,所以BC∥PE(同位角相等,两直线平行).
3. 解:∠3=55°,AB∥CD,理由:因为∠3=∠2,∠1=∠2=55°,所以∠1=∠3=55°,所以AB∥CD.
4. C
5. 平行 (1)同位角相等,两条直线平行 (2)在同一平面内,垂直于同一条直线的两条直线平行
6. B 7. B 8. B 9. C 10. A
11. 4
12. 平行
13. 垂直 平行 平行
14. 解:如图所示. EF为所求作的图形.
15. 解:EC∥DF. 理由:因为∠ABC=∠ACB,∠1=∠2,所以∠3=∠ECB. 因为∠3=∠F,所以∠ECB=∠F,所以EC∥DF.
16. 解:由图(1)可知,
因为AB⊥PE,CD⊥PE,所以AB∥CD(即同一平面内垂直于同一条直线的两条直线互相平行).
由图(2)可知,因为AB⊥PE,CD⊥PE,所以∠1=∠2=90°,所以AB∥CD(即同位角相等,两直线平行).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
沪科版数学七年级下册同步课时训练
第10章 相交线、平行线与平移
10.2 平行线的判定
第2课时 平行线的判定(一)
要点测评 基础达标
要点1 同位角相等两直线平行
1. 如图,给出了过直线外一点作已知直线的平行线的方法,其依据是 .
2. 如图,∠1=∠C,∠2=∠E,指出图中哪些直线是平行的,并说出理由.
3. 如图,∠1=∠2=55°,∠3等于多少度?直线AB,CD平行吗?说明理由.
要点2 在同一平面内垂直于同一直线的两直线平行
4. 同一平面内的四条直线若满足a⊥b,b⊥c,c⊥d,则下列式子成立的是( )
A. a∥d B. b⊥d C. a⊥d D. b∥c
5. 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线 .?
图1 图2
(1)它的理由如下:(如图1)
因为b⊥a,c⊥a,所以∠1=∠2=90°,
所以b∥c( )?
(2)如图2是木工师傅使用角尺画平行线,有什么道理?
.?
课后集训 巩固提升
6. 如图,直线a,b被直线c所截,下列条件能判断a∥b的是( )
A. ∠1=∠2 B. ∠1=∠4
C. ∠3+∠4=180° D. ∠2=30°,∠4=35°
7. 如图,已知∠C=70°,当∠AED等于多少时,DE∥BC( )
A. 20° B. 70° C. 110° D. 180°
8. 下列说法中,正确的有( )
①在同一平面内,若a与c相交,b与c相交,则a∥b;②在同一平面内,若a⊥c,b⊥c,则a∥b;③在同一平面内,若a∥c,b∥c,则a∥b;④在同一平面内,若a⊥c,b∥c,则a∥b.
A. 1个 B. 2个 C. 3个 D. 4个
9. 根据如图与已知条件,指出下列推断错误的是( )
A. 由∠1=∠2,得AB∥CD B. 由∠1+∠3=∠2+∠4,得AE∥CN
C. 由∠5=∠6,∠3=∠4,得AB∥CD D. 由∠SAB=∠SCD,得AB∥CD
10. 在同一平面内,有8条互不重合的直线,l1,l2,l3…l8,若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5…以此类推,则l1和l8的位置关系是( )
A. 平行 B. 垂直 C. 平行或垂直 D. 无法确定
11. 能判定DE∥BC的同位角有 组.?
12. 如图,已知∠1=55°,∠2=35°,点O在直线a上,且OA⊥OB,则a与b的位置关系是 .?
13. 设a,b,l为平面内三条不同直线.①若a∥b,l⊥a,则l与b的位置关系是 ;②若l⊥a,l⊥b,则a与b的位置关系是 ;③若a∥b,l∥a,则l与b的位置关系是 .?
14. 我们已经掌握“在同一平面内,垂直于同一条直线的两条直线互相平行”这一判定两直线平行的方法.如图,已知直线AB和直线外一点C,请按照上述方法利用三角尺过点C画AB的平行线.(保留作图痕迹,不用写作法)
15. 如图,已知∠ABC=∠ACB,∠1=∠2,∠3=∠F,试判断EC与DF是否平行,并说明理由.
16. 学习了平行线后,小敏想出了过已知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如图(1)~(4)).从图中操作过程你知道小敏画平行线的依据吗?请把你的想法写出来.
参 考 答 案
1. 同位角相等,两直线平行
2. 解:AC∥DP,BC∥PE,理由是:因为∠1=∠C,所以AC∥DP(同位角相等,两直线平行),因为∠2=∠E,所以BC∥PE(同位角相等,两直线平行).
3. 解:∠3=55°,AB∥CD,理由:因为∠3=∠2,∠1=∠2=55°,所以∠1=∠3=55°,所以AB∥CD.
4. C
5. 平行 (1)同位角相等,两条直线平行 (2)在同一平面内,垂直于同一条直线的两条直线平行
6. B 7. B 8. B 9. C 10. A
11. 4
12. 平行
13. 垂直 平行 平行
14. 解:如图所示. EF为所求作的图形.
15. 解:EC∥DF. 理由:因为∠ABC=∠ACB,∠1=∠2,所以∠3=∠ECB. 因为∠3=∠F,所以∠ECB=∠F,所以EC∥DF.
16. 解:由图(1)可知,
因为AB⊥PE,CD⊥PE,所以AB∥CD(即同一平面内垂直于同一条直线的两条直线互相平行).
由图(2)可知,因为AB⊥PE,CD⊥PE,所以∠1=∠2=90°,所以AB∥CD(即同位角相等,两直线平行).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
