10.2.1 平行线的概念及基本性质(要点测评+课后集训+答案)
文档属性
| 名称 | 10.2.1 平行线的概念及基本性质(要点测评+课后集训+答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-24 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
沪科版数学七年级下册同步课时训练
第10章 相交线、平行线与平移
10.2 平行线的判定
第1课时 平行线的概念及基本性质
要点测评 基础达标
要点1 平行线的概念
1. 下列说法正确的是( )
A. 同一个平面内,不相交的两条线段是平行线
B. 同一个平面内,两条直线不相交就重合
C. 同一个平面内,没有公共点的两条直线是平行线
D. 不相交的两条直线是平行线
2. 在同一平面内,两条不重合直线的位置关系可能是( )
A. 垂直或平行 B. 垂直或相交
C. 平行或相交 D. 平行、垂直或相交
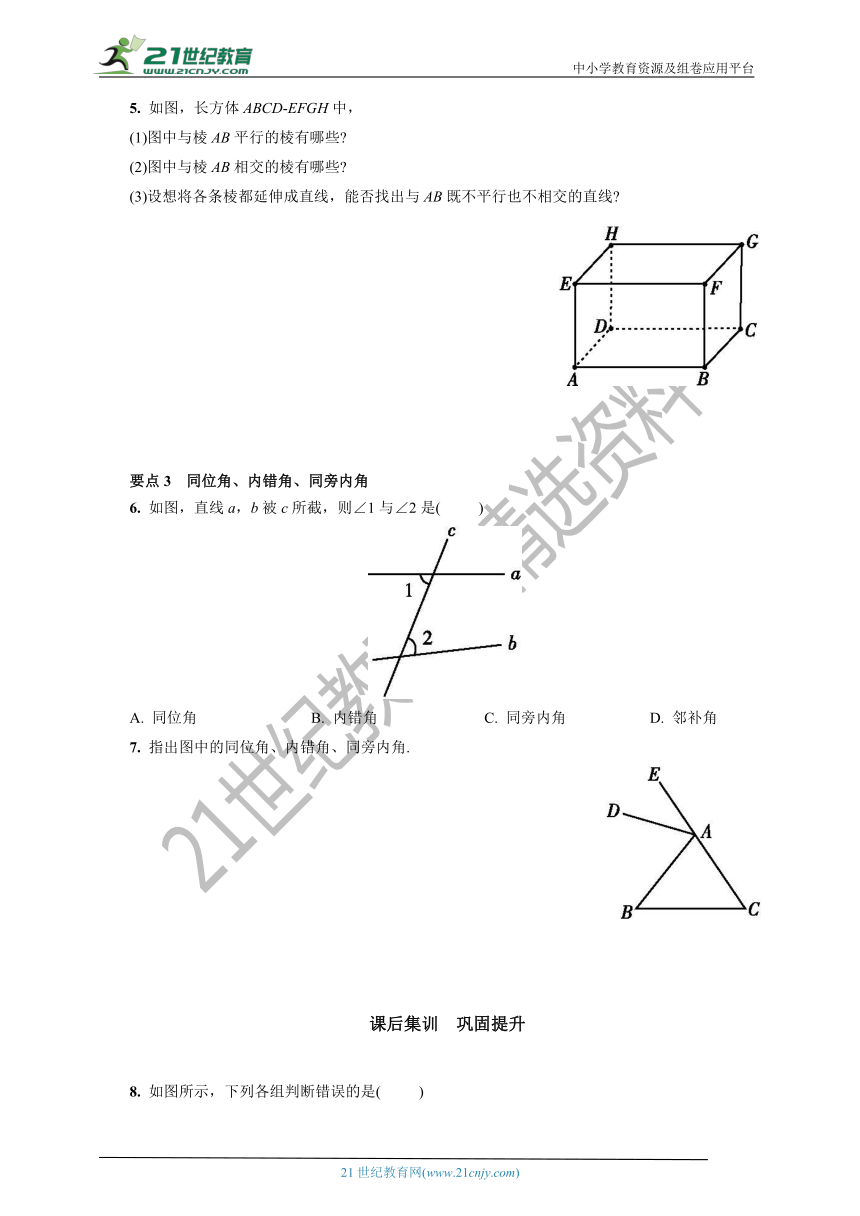
3. 根据下列要求画图.
(1)如图①所示,过点A画MN∥BC;
(2)如图②所示,过点C画CE∥DA,与AB交于点E,过点C画CF∥DB,与AB的延长线交于点F.
要点2 平行线的基本性质
4. 现有下列语句:①过一点有且只有一条直线与已知直线平行;②若直线a∥b,b∥c,则a∥c;③过两条直线a,b外一点P,可画出直线c,使c∥a且c∥b.其中正确的有( )
A. 0个 B. 1个 C. 2个 D. 3个
5. 如图,长方体ABCD-EFGH中,
(1)图中与棱AB平行的棱有哪些?
(2)图中与棱AB相交的棱有哪些?
(3)设想将各条棱都延伸成直线,能否找出与AB既不平行也不相交的直线?
要点3 同位角、内错角、同旁内角
6. 如图,直线a,b被c所截,则∠1与∠2是( )
A. 同位角 B. 内错角 C. 同旁内角 D. 邻补角
7. 指出图中的同位角、内错角、同旁内角.
课后集训 巩固提升
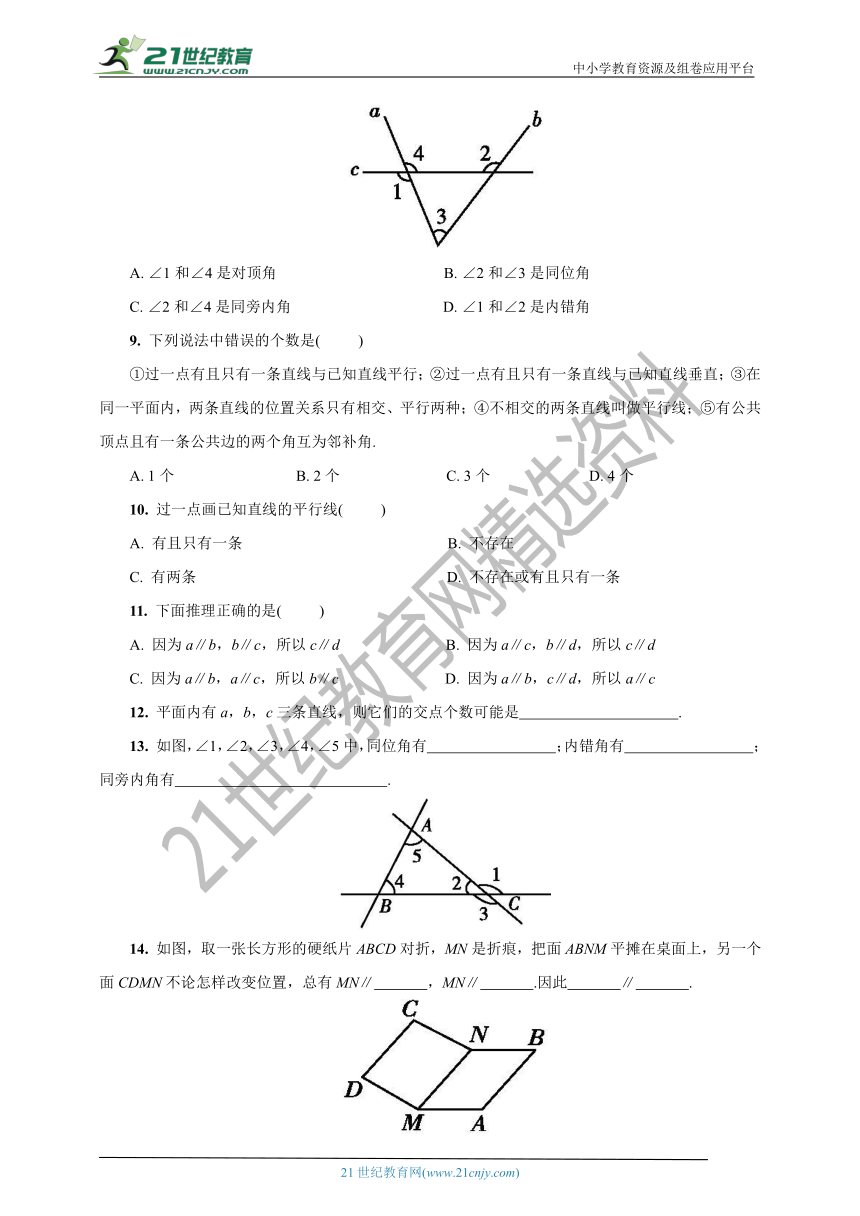
8. 如图所示,下列各组判断错误的是( )
A. ∠1和∠4是对顶角 B. ∠2和∠3是同位角
C. ∠2和∠4是同旁内角 D. ∠1和∠2是内错角
9. 下列说法中错误的个数是( )
①过一点有且只有一条直线与已知直线平行;②过一点有且只有一条直线与已知直线垂直;③在同一平面内,两条直线的位置关系只有相交、平行两种;④不相交的两条直线叫做平行线;⑤有公共顶点且有一条公共边的两个角互为邻补角.
A. 1个 B. 2个 C. 3个 D. 4个
10. 过一点画已知直线的平行线( )
A. 有且只有一条 B. 不存在
C. 有两条 D. 不存在或有且只有一条
11. 下面推理正确的是( )
A. 因为a∥b,b∥c,所以c∥d B. 因为a∥c,b∥d,所以c∥d
C. 因为a∥b,a∥c,所以b∥c D. 因为a∥b,c∥d,所以a∥c
12. 平面内有a,b,c三条直线,则它们的交点个数可能是 .?
13. 如图,∠1,∠2,∠3,∠4,∠5中,同位角有 ;内错角有 ;同旁内角有 .?
14. 如图,取一张长方形的硬纸片ABCD对折,MN是折痕,把面ABNM平摊在桌面上,另一个面CDMN不论怎样改变位置,总有MN∥ ,MN∥ .因此 ∥ .?
15. 如图所示,如果内错角∠1与∠5相等,那么与∠1相等的角还有吗?与∠1互补的角有吗?如果有,请写出来,并说明你的理由.
16. 过点M,N分别画直线AB的平行线,判断所画的两条直线的位置关系.
17. 如图,三条直线两两相交,形成12个角,其中同位角共有几对?内错角共有几对?同旁内角共有几对?
18. 如图所示,在∠AOB内有一点P.
(1)过P画l1∥OA;
(2)过P画l2∥OB;
(3)用量角器量一量l1与l2相交的角与∠O的大小有怎样关系?
参 考 答 案
1. C 2. C
3. 解:如图所示:
4. B
5. 解:(1)与棱AB平行的棱有CD,EF,HG;
(2)与棱AB相交的棱有AD,BC,AE,BF;
(3)能,EH和FG还有HD和CG都是与AB既不平行也不相交的直线.
6. B
7. 解:2对内错角:∠DAB和∠B,∠B和∠BAE;2对同位角:∠DAE和∠C,∠BAE和∠C;4对同旁内角:∠CAD和∠C,∠B和∠C,∠B和∠BAC,∠C和∠BAC.
8. D 9. D 10. D 11. C
12. 0或1个或2个或3个
13. ∠1与∠4,∠5与∠3 ∠3与∠4,∠1与∠5 ∠2与∠4,∠2与∠5,∠4与∠5
14. DC AB DC AB
15. 解:∠1=∠2,∠1+∠3=∠1+∠4=180°. 理由如下:因为∠1=∠5,∠5=∠2,所以∠1=∠2. 因为∠1=∠5,且∠5与∠3或∠4互补,所以与∠1互补的角还有∠3和∠4.
16. 解:作图如图CD,EF.
CD∥EF.理由如下:因为AB∥CD,AB∥EF,所以CD∥EF(如果两条直线都和第三条直线平行,那么这两条直线平行).
17. 解:同位角共有12对,内错角共有6对,同旁内角共有6对.
18. 解:(1)(2)如图所示.
(3)l1与l2夹角有两个:∠1,∠2;∠1=∠O,∠2+∠O=180°,所以l1和l2的夹角与∠O相等或互补.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
沪科版数学七年级下册同步课时训练
第10章 相交线、平行线与平移
10.2 平行线的判定
第1课时 平行线的概念及基本性质
要点测评 基础达标
要点1 平行线的概念
1. 下列说法正确的是( )
A. 同一个平面内,不相交的两条线段是平行线
B. 同一个平面内,两条直线不相交就重合
C. 同一个平面内,没有公共点的两条直线是平行线
D. 不相交的两条直线是平行线
2. 在同一平面内,两条不重合直线的位置关系可能是( )
A. 垂直或平行 B. 垂直或相交
C. 平行或相交 D. 平行、垂直或相交
3. 根据下列要求画图.
(1)如图①所示,过点A画MN∥BC;
(2)如图②所示,过点C画CE∥DA,与AB交于点E,过点C画CF∥DB,与AB的延长线交于点F.
要点2 平行线的基本性质
4. 现有下列语句:①过一点有且只有一条直线与已知直线平行;②若直线a∥b,b∥c,则a∥c;③过两条直线a,b外一点P,可画出直线c,使c∥a且c∥b.其中正确的有( )
A. 0个 B. 1个 C. 2个 D. 3个
5. 如图,长方体ABCD-EFGH中,
(1)图中与棱AB平行的棱有哪些?
(2)图中与棱AB相交的棱有哪些?
(3)设想将各条棱都延伸成直线,能否找出与AB既不平行也不相交的直线?
要点3 同位角、内错角、同旁内角
6. 如图,直线a,b被c所截,则∠1与∠2是( )
A. 同位角 B. 内错角 C. 同旁内角 D. 邻补角
7. 指出图中的同位角、内错角、同旁内角.
课后集训 巩固提升
8. 如图所示,下列各组判断错误的是( )
A. ∠1和∠4是对顶角 B. ∠2和∠3是同位角
C. ∠2和∠4是同旁内角 D. ∠1和∠2是内错角
9. 下列说法中错误的个数是( )
①过一点有且只有一条直线与已知直线平行;②过一点有且只有一条直线与已知直线垂直;③在同一平面内,两条直线的位置关系只有相交、平行两种;④不相交的两条直线叫做平行线;⑤有公共顶点且有一条公共边的两个角互为邻补角.
A. 1个 B. 2个 C. 3个 D. 4个
10. 过一点画已知直线的平行线( )
A. 有且只有一条 B. 不存在
C. 有两条 D. 不存在或有且只有一条
11. 下面推理正确的是( )
A. 因为a∥b,b∥c,所以c∥d B. 因为a∥c,b∥d,所以c∥d
C. 因为a∥b,a∥c,所以b∥c D. 因为a∥b,c∥d,所以a∥c
12. 平面内有a,b,c三条直线,则它们的交点个数可能是 .?
13. 如图,∠1,∠2,∠3,∠4,∠5中,同位角有 ;内错角有 ;同旁内角有 .?
14. 如图,取一张长方形的硬纸片ABCD对折,MN是折痕,把面ABNM平摊在桌面上,另一个面CDMN不论怎样改变位置,总有MN∥ ,MN∥ .因此 ∥ .?
15. 如图所示,如果内错角∠1与∠5相等,那么与∠1相等的角还有吗?与∠1互补的角有吗?如果有,请写出来,并说明你的理由.
16. 过点M,N分别画直线AB的平行线,判断所画的两条直线的位置关系.
17. 如图,三条直线两两相交,形成12个角,其中同位角共有几对?内错角共有几对?同旁内角共有几对?
18. 如图所示,在∠AOB内有一点P.
(1)过P画l1∥OA;
(2)过P画l2∥OB;
(3)用量角器量一量l1与l2相交的角与∠O的大小有怎样关系?
参 考 答 案
1. C 2. C
3. 解:如图所示:
4. B
5. 解:(1)与棱AB平行的棱有CD,EF,HG;
(2)与棱AB相交的棱有AD,BC,AE,BF;
(3)能,EH和FG还有HD和CG都是与AB既不平行也不相交的直线.
6. B
7. 解:2对内错角:∠DAB和∠B,∠B和∠BAE;2对同位角:∠DAE和∠C,∠BAE和∠C;4对同旁内角:∠CAD和∠C,∠B和∠C,∠B和∠BAC,∠C和∠BAC.
8. D 9. D 10. D 11. C
12. 0或1个或2个或3个
13. ∠1与∠4,∠5与∠3 ∠3与∠4,∠1与∠5 ∠2与∠4,∠2与∠5,∠4与∠5
14. DC AB DC AB
15. 解:∠1=∠2,∠1+∠3=∠1+∠4=180°. 理由如下:因为∠1=∠5,∠5=∠2,所以∠1=∠2. 因为∠1=∠5,且∠5与∠3或∠4互补,所以与∠1互补的角还有∠3和∠4.
16. 解:作图如图CD,EF.
CD∥EF.理由如下:因为AB∥CD,AB∥EF,所以CD∥EF(如果两条直线都和第三条直线平行,那么这两条直线平行).
17. 解:同位角共有12对,内错角共有6对,同旁内角共有6对.
18. 解:(1)(2)如图所示.
(3)l1与l2夹角有两个:∠1,∠2;∠1=∠O,∠2+∠O=180°,所以l1和l2的夹角与∠O相等或互补.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
