人教版数学必修三第二章2.2.1 用样本的频率分布估计总体分布课件(共34张PPT)
文档属性
| 名称 | 人教版数学必修三第二章2.2.1 用样本的频率分布估计总体分布课件(共34张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 310.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-25 22:41:54 | ||
图片预览








文档简介
(共34张PPT)
用样本的频率分布估计总体分布
统计的基本思想方法
用样本估计总体,即通常不直接去研究总体,而是通过从总体中抽取一个样本,根据样本的情况去估计总体的相应情况.
统计的核心问题
如何根据样本的情况对总体的情况作出推断.这里包括两类问题:
一类是如何从总体中抽取样本?
另一类是如何根据对样本的整理、计算、分析, 对总体的情况作出推断.
用样本的有关情况去估计总体的相应情况,
大体分为两类:
一类是用样本频率分布估计总体分布;
一类是用样本的某种数字特征(例如平均数、方差等)去估计总体的相应数字特征。
整体介绍
用样本频率分布估计总体分布
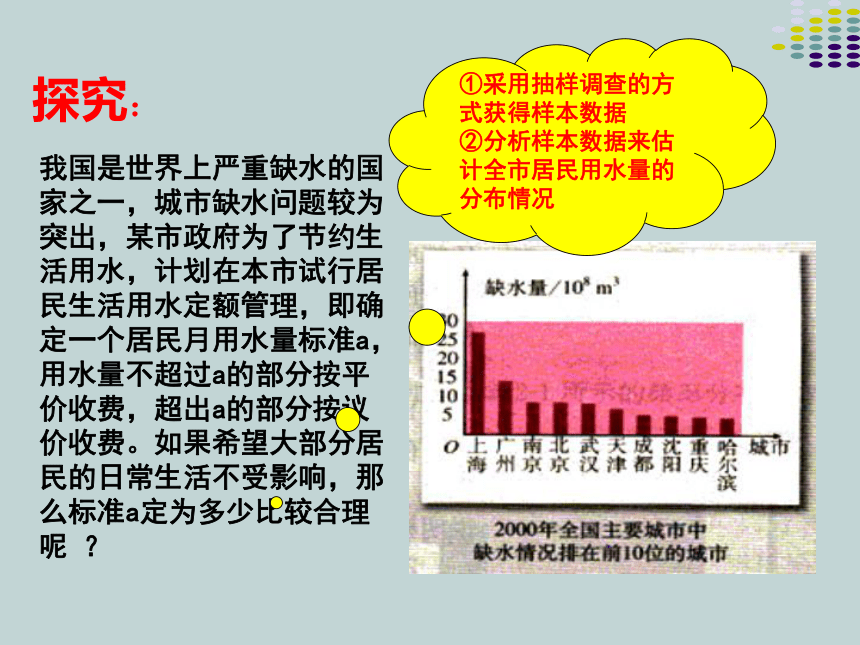
我国是世界上严重缺水的国家之一,城市缺水问题较为突出,某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a,用水量不超过a的部分按平价收费,超出a的部分按议价收费。如果希望大部分居民的日常生活不受影响,那么标准a定为多少比较合理呢 ?
探究:
你认为,为了较为合理地确定出这个标准,需要做哪些工作?
我国是世界上严重缺水的国家之一,城市缺水问题较为突出,某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a,用水量不超过a的部分按平价收费,超出a的部分按议价收费。如果希望大部分居民的日常生活不受影响,那么标准a定为多少比较合理呢 ?
探究:
①采用抽样调查的方式获得样本数据
②分析样本数据来估计全市居民用水量的分布情况
下表给出100位居民的月均用水量表
分析数据的一种基本方法是用图将它们画出来,或者用紧凑的表格改变数据的排列方式,作图可以达到两个目的,一是从数据中提取信息,二是利用图形传递信息。表格则是通过改变数据的构成形式,为我们提供解释数据的新方式
讨论:如何分析数据?
根据这些数据你能得出用水量其他信息吗?
为此我们要对这些数据进行整理与分析
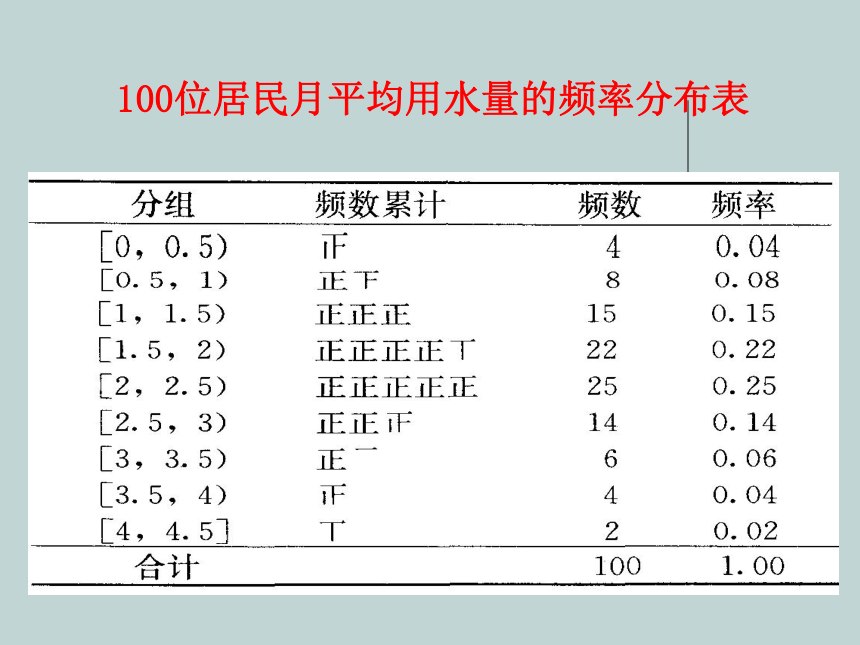
100位居民月平均用水量的频率分布表
〈一〉频率分布的概念:
频率分布是指一个样本数据在各个小范围内所占比例的大小。一般用频率分布直方图反映样本的频率分布
〈二〉画频率分布直方图其一般步骤为
(1)计算一组数据中最大值与最小值的差,即求极差
(2)决定组距与组数
(3)将数据分组
(4)列频率分布表
(5)画频率分布直方图
第一步: 求极差: (数据组中最大值与最小值的差距)
最大值= 4.3 最小值= 0.2
所以极差= 4.3-0.2 = 4.1
第二步: 决定组距与组数: (强调取整)
当样本容量不超过100时, 按照数据的多少, 常分成5~12组.
为方便组距的选择应力求”取整”.
本题如果组距为0.5(t). 则
第三步: 将数据分组:( 给出组的界限)
所以将数据分成9组较合适.
[0, 0.5), [0.5, 1), [1, 1.5),……[4, 4.5) 共9组.
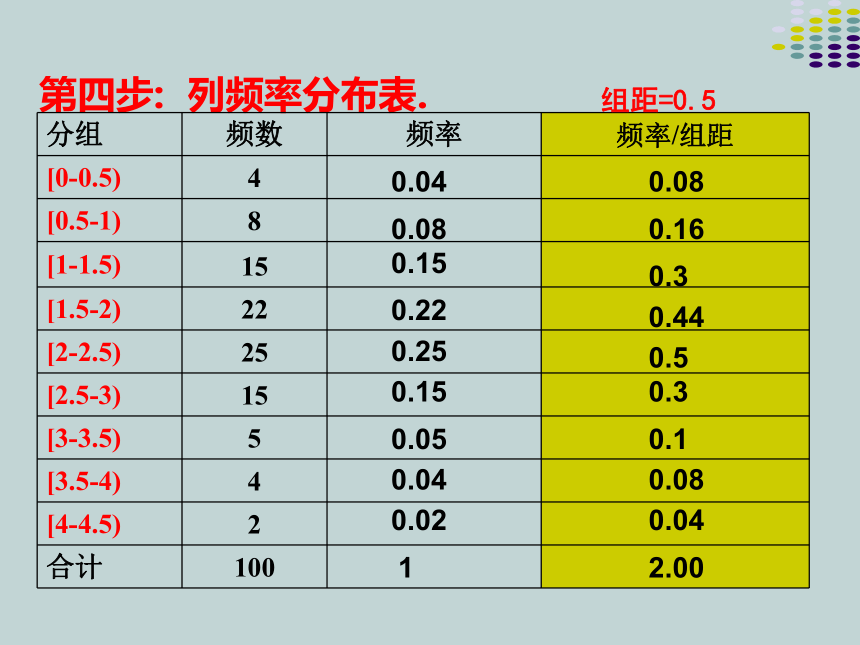
第四步: 列频率分布表.
分组 频数 频率 频率/组距
[0-0.5) 4
[0.5-1) 8
[1-1.5) 15
[1.5-2) 22
[2-2.5) 25
[2.5-3) 15
[3-3.5) 5
[3.5-4) 4
[4-4.5) 2
合计 100
组距=0.5
0.04
0.08
0.08
0.16
0.3
0.15
0.44
0.22
0.25
0.5
1
2.00
0.02
0.04
0.04
0.08
0.1
0.3
0.15
0.05
0
0.1
0.2
0.3
0.4
0.5
0.6
0.5 1 1.5 2 2.5 3 3.5 4 4.5
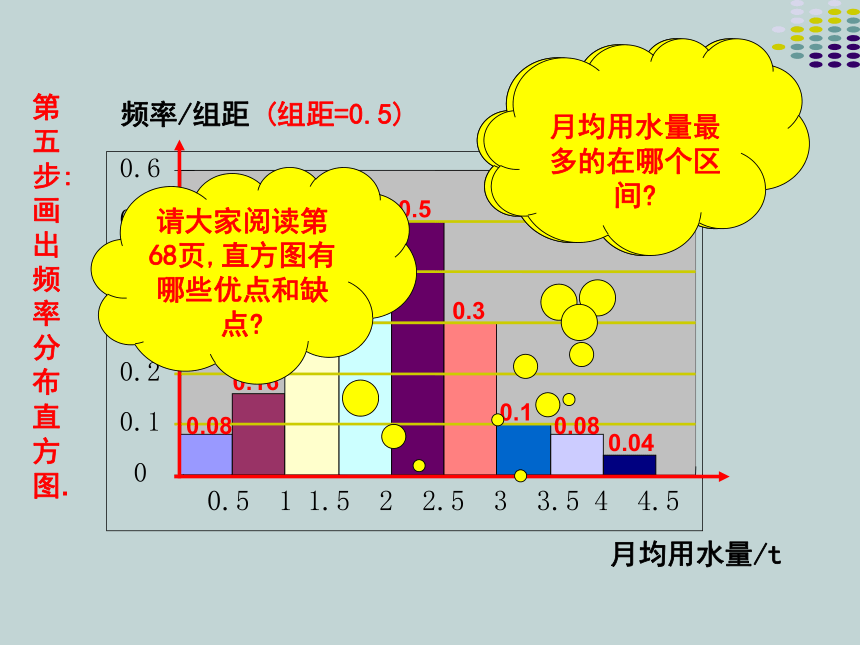
第五步: 画出频率分布直方图.
频率/组距
月均用水量/t
(组距=0.5)
0.08
0.16
0.3
0.44
0.5
0.3
0.1
0.08
0.04
小长方形的面积=?
小长方形的面积总和=?
月均用水量最多的在哪个区间?
请大家阅读第68页,直方图有哪些优点和缺点?
频率分布直方图的特征:
从频率分布直方图可以清楚的看出数据分布的总体趋势。
从频率分布直方图得不出原始的数据内容,把数据表示成直方图后,原有的具体数据信息就被抹掉了。
思考:
1.频率分布表与频率分布直方图的区别?
频率分布表列出的是在各个不同区间内取值的频率。
频率分布直方图是用小长方形面积的大小来表示在各个区间内取值的频率。
2.如果当地政府希望使85%以上的居民每月的用水量不
超出标准,根据频率分布表2-2和频率分布直方图2.2-1,
你能对制定月用水量标准提出建议吗 ?
3.将组距确定为1,作出教材P66页 居民月均用水量的频率分布直方图
4.谈谈两种组距下,你对图的印象?同一个样本数据,绘制出来的分布图是唯一的吗?
(同样一组数据,如果组距不同,横轴、纵轴的单位不同,得到的图和形状也会不同。不同的形状给人以不同的印象,这种印象有时会影响我们对总体的判断 )
(一)频率分布折线图:
画好频率分布图后,我们把频率分布直方图中各小长
方形上端连接起来,得到的图形.
0
0.1
0.2
0.3
0.4
0.5
0.6
0.5 1 1.5 2 2.5 3 3.5 4 4.5
画出频率分布折线图.
频率/组距
月均用水量/t
(取组距中点, 并连线 )
0.08
0.16
0.3
0.44
0.5
0.3
0.1
0.08
0.04
在样本频率分布直方图中,当样本容量增加,作图时所分的组数增加,组距减少,相应的频率折线图会越来越接近于一条光滑曲线,统计中称这条光滑曲线为总体密度曲线. 它能够精确地反映了总体在各个范围内取值的百分比,它能给我们提供更加精细的信息.
总体密度曲线:
月均用水量/t
频率
组距
0
a
b
月均用水量/t
频率
组距
0
a
b
1.对于任何一个总体,它的密度曲线是不是一定存在?它的密度曲线是否可以被非常准确地画出来?
思考
2.图中阴影部分的面积表示什么?
2.总体在范围(a,b)内取值的百分比
月均用水量/t
频率
组距
0
a
b
1.实际上,尽管有些总体密度曲线是客观存在的,但一般很难想函数图象那样准确地画出来,我们只能用样本的频率分布对它进行估计,一般来说,样本容量越大,这种估计就越精确
(二)茎叶图
当数据是两位有效数字时,用中间的数字表示十位数,即第一个有效数字,两边的数字表示个位数,即第二个有效数字,它的中间部分像植物的茎,两边部分像植物茎上长出来的叶子,因此通常把这样的图叫做茎叶图
例: 甲乙两人比赛得分记录如下:
甲:13, 51, 23, 8, 26, 38, 16, 33, 14, 28, 39
乙:49, 24, 12, 31, 50, 31, 44, 36, 15, 37, 25, 36, 39
用茎叶图表示两人成绩,说明哪一个成绩好.
甲 乙
0
1
2
3
4
5
2, 5
5, 4
1, 6, 1, 6, 7, 9
4, 9
0
8
4, 6, 3
3, 6, 8
3, 8, 9
1
叶 茎 叶
(二). 茎叶图 (一种被用来表示数据的图)
画茎叶图的步骤:
1.将每个数据分为茎(高位)和叶(低位)两部分,在此例中,茎为十
位上的数字,叶为个位上的数字;
2.将最小茎和最大茎之间的数按大小次序排成一列,写在左(右)
侧;
3.将各个数据的叶按大小次序
写在其茎右(左)侧.
茎 叶
0 8
1 3 4 5
2 3 6 8
3 3 8 9
4
5 1
(1)用茎叶图表示数据有两个优点:一是从统计图上没有原始数据信息的损失,所有数据信息都可以从茎叶图中得到;二是茎叶图中的数据可以随时记录,随时添加,方便记录与表示。
(2)茎叶图只便于表示两位有效数字的数据,而且茎叶图只方便记录两组的数据,两个以上的数据虽然能够记录,但是没有表示两个记录那么直观,清晰。
茎叶图的特征:
练 习:
1.有一个容量为50的样本数据的分组的频数如下:
[12.5, 15.5) 3
[15.5, 18.5) 8
[18.5, 21.5) 9
[21.5, 24.5) 11
[24.5, 27.5) 10
[27.5, 30.5) 5
[30.5, 33.5) 4
(1)列出样本的频率分布表;
(2)画出频率分布直方图;
(3)根据频率分布直方图估计,数据落在[15.5, 24.5)的百分比是多少?
解:组距为3
分组 频数 频率 频率/ 组距
[12.5, 15.5) 3
[15.5, 18.5) 8
[18.5, 21.5) 9
[21.5, 24.5) 11
[24.5, 27.5) 10
[27.5, 30.5) 5
[30.5, 33.5) 4
0.06
0.16
0.18
0.22
0.20
0.10
0.08
0.020
0.053
0.060
0.073
0.067
0.033
0.027
频率分布直方图如下:
频率
组距
0.010
0.020
0.030
0.040
0.050
12.5
15.5
0.060
0.070
练习:2 .投掷一枚均匀骰子44次的记录是:
3 2 4 1 5 1 3 4 5 6 5
4 2 5 3 1 3 4 1 4 5 1
6 3 3 1 2 4 2 6 3 4 6
6 1 6 2 2 5 2 6 5 4 3
现对这些数据进行整理,试画出频数分布直方图.
第一步:写出样本可能出现的一切数值,即:
1,2,3,4,5,6 共6个数.(数据分组)
第二步:列出频率分布表:
样本 1 2 3 4 5 6
频数 7 7 8 8 7 7
频率 0.16 0.16 0.18 0.18 0.16 0.16
组距=1
第三步: 画频率分布直方图
频数 茎 叶
2 10 7, 8
11 11 2, 7, 6, 3, 6, 8, 6, 7, 2, 2,0
13 12 6, 8, 4, 2, 7, 8, 6, 1, 0, 4, 3, 2, 0
4 13 4, 2, 3, 0
下表一组数据是某车间30名工人加工零件的个数, 设计一个
茎叶图表示这组数据,并说明这一车间的生产情况.
134 112 117 126 128 124 122 116 113 107
116 132 127 128 126 121 120 118 108 110
133 130 124 116 117 123 122 120 112 112
练习:
小结:
画频率分布直方图的步骤:
第一步: 求极差: (数据组中最大值与最小值的差距)
第二步: 决定组距与组数: (强调取整)
第三步: 将数据分组 ( 给出组的界限)
第四步: 列频率分布表. (包括分组、频数、频率、频率/组距)
第五步: 画频率分布直方图(在频率分布表的基础上绘制,横坐标为样本数据尺寸,纵坐标为频率/组距.)
组距:指每个小组的两个端点的距离,组距
组数:将数据分组,当数据在100个以内时,
按数据多少常分5-12组。
作业:P71第一题 习题2.2:2
注意
(2)纵坐标为:
再见
用样本的频率分布估计总体分布
统计的基本思想方法
用样本估计总体,即通常不直接去研究总体,而是通过从总体中抽取一个样本,根据样本的情况去估计总体的相应情况.
统计的核心问题
如何根据样本的情况对总体的情况作出推断.这里包括两类问题:
一类是如何从总体中抽取样本?
另一类是如何根据对样本的整理、计算、分析, 对总体的情况作出推断.
用样本的有关情况去估计总体的相应情况,
大体分为两类:
一类是用样本频率分布估计总体分布;
一类是用样本的某种数字特征(例如平均数、方差等)去估计总体的相应数字特征。
整体介绍
用样本频率分布估计总体分布
我国是世界上严重缺水的国家之一,城市缺水问题较为突出,某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a,用水量不超过a的部分按平价收费,超出a的部分按议价收费。如果希望大部分居民的日常生活不受影响,那么标准a定为多少比较合理呢 ?
探究:
你认为,为了较为合理地确定出这个标准,需要做哪些工作?
我国是世界上严重缺水的国家之一,城市缺水问题较为突出,某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a,用水量不超过a的部分按平价收费,超出a的部分按议价收费。如果希望大部分居民的日常生活不受影响,那么标准a定为多少比较合理呢 ?
探究:
①采用抽样调查的方式获得样本数据
②分析样本数据来估计全市居民用水量的分布情况
下表给出100位居民的月均用水量表
分析数据的一种基本方法是用图将它们画出来,或者用紧凑的表格改变数据的排列方式,作图可以达到两个目的,一是从数据中提取信息,二是利用图形传递信息。表格则是通过改变数据的构成形式,为我们提供解释数据的新方式
讨论:如何分析数据?
根据这些数据你能得出用水量其他信息吗?
为此我们要对这些数据进行整理与分析
100位居民月平均用水量的频率分布表
〈一〉频率分布的概念:
频率分布是指一个样本数据在各个小范围内所占比例的大小。一般用频率分布直方图反映样本的频率分布
〈二〉画频率分布直方图其一般步骤为
(1)计算一组数据中最大值与最小值的差,即求极差
(2)决定组距与组数
(3)将数据分组
(4)列频率分布表
(5)画频率分布直方图
第一步: 求极差: (数据组中最大值与最小值的差距)
最大值= 4.3 最小值= 0.2
所以极差= 4.3-0.2 = 4.1
第二步: 决定组距与组数: (强调取整)
当样本容量不超过100时, 按照数据的多少, 常分成5~12组.
为方便组距的选择应力求”取整”.
本题如果组距为0.5(t). 则
第三步: 将数据分组:( 给出组的界限)
所以将数据分成9组较合适.
[0, 0.5), [0.5, 1), [1, 1.5),……[4, 4.5) 共9组.
第四步: 列频率分布表.
分组 频数 频率 频率/组距
[0-0.5) 4
[0.5-1) 8
[1-1.5) 15
[1.5-2) 22
[2-2.5) 25
[2.5-3) 15
[3-3.5) 5
[3.5-4) 4
[4-4.5) 2
合计 100
组距=0.5
0.04
0.08
0.08
0.16
0.3
0.15
0.44
0.22
0.25
0.5
1
2.00
0.02
0.04
0.04
0.08
0.1
0.3
0.15
0.05
0
0.1
0.2
0.3
0.4
0.5
0.6
0.5 1 1.5 2 2.5 3 3.5 4 4.5
第五步: 画出频率分布直方图.
频率/组距
月均用水量/t
(组距=0.5)
0.08
0.16
0.3
0.44
0.5
0.3
0.1
0.08
0.04
小长方形的面积=?
小长方形的面积总和=?
月均用水量最多的在哪个区间?
请大家阅读第68页,直方图有哪些优点和缺点?
频率分布直方图的特征:
从频率分布直方图可以清楚的看出数据分布的总体趋势。
从频率分布直方图得不出原始的数据内容,把数据表示成直方图后,原有的具体数据信息就被抹掉了。
思考:
1.频率分布表与频率分布直方图的区别?
频率分布表列出的是在各个不同区间内取值的频率。
频率分布直方图是用小长方形面积的大小来表示在各个区间内取值的频率。
2.如果当地政府希望使85%以上的居民每月的用水量不
超出标准,根据频率分布表2-2和频率分布直方图2.2-1,
你能对制定月用水量标准提出建议吗 ?
3.将组距确定为1,作出教材P66页 居民月均用水量的频率分布直方图
4.谈谈两种组距下,你对图的印象?同一个样本数据,绘制出来的分布图是唯一的吗?
(同样一组数据,如果组距不同,横轴、纵轴的单位不同,得到的图和形状也会不同。不同的形状给人以不同的印象,这种印象有时会影响我们对总体的判断 )
(一)频率分布折线图:
画好频率分布图后,我们把频率分布直方图中各小长
方形上端连接起来,得到的图形.
0
0.1
0.2
0.3
0.4
0.5
0.6
0.5 1 1.5 2 2.5 3 3.5 4 4.5
画出频率分布折线图.
频率/组距
月均用水量/t
(取组距中点, 并连线 )
0.08
0.16
0.3
0.44
0.5
0.3
0.1
0.08
0.04
在样本频率分布直方图中,当样本容量增加,作图时所分的组数增加,组距减少,相应的频率折线图会越来越接近于一条光滑曲线,统计中称这条光滑曲线为总体密度曲线. 它能够精确地反映了总体在各个范围内取值的百分比,它能给我们提供更加精细的信息.
总体密度曲线:
月均用水量/t
频率
组距
0
a
b
月均用水量/t
频率
组距
0
a
b
1.对于任何一个总体,它的密度曲线是不是一定存在?它的密度曲线是否可以被非常准确地画出来?
思考
2.图中阴影部分的面积表示什么?
2.总体在范围(a,b)内取值的百分比
月均用水量/t
频率
组距
0
a
b
1.实际上,尽管有些总体密度曲线是客观存在的,但一般很难想函数图象那样准确地画出来,我们只能用样本的频率分布对它进行估计,一般来说,样本容量越大,这种估计就越精确
(二)茎叶图
当数据是两位有效数字时,用中间的数字表示十位数,即第一个有效数字,两边的数字表示个位数,即第二个有效数字,它的中间部分像植物的茎,两边部分像植物茎上长出来的叶子,因此通常把这样的图叫做茎叶图
例: 甲乙两人比赛得分记录如下:
甲:13, 51, 23, 8, 26, 38, 16, 33, 14, 28, 39
乙:49, 24, 12, 31, 50, 31, 44, 36, 15, 37, 25, 36, 39
用茎叶图表示两人成绩,说明哪一个成绩好.
甲 乙
0
1
2
3
4
5
2, 5
5, 4
1, 6, 1, 6, 7, 9
4, 9
0
8
4, 6, 3
3, 6, 8
3, 8, 9
1
叶 茎 叶
(二). 茎叶图 (一种被用来表示数据的图)
画茎叶图的步骤:
1.将每个数据分为茎(高位)和叶(低位)两部分,在此例中,茎为十
位上的数字,叶为个位上的数字;
2.将最小茎和最大茎之间的数按大小次序排成一列,写在左(右)
侧;
3.将各个数据的叶按大小次序
写在其茎右(左)侧.
茎 叶
0 8
1 3 4 5
2 3 6 8
3 3 8 9
4
5 1
(1)用茎叶图表示数据有两个优点:一是从统计图上没有原始数据信息的损失,所有数据信息都可以从茎叶图中得到;二是茎叶图中的数据可以随时记录,随时添加,方便记录与表示。
(2)茎叶图只便于表示两位有效数字的数据,而且茎叶图只方便记录两组的数据,两个以上的数据虽然能够记录,但是没有表示两个记录那么直观,清晰。
茎叶图的特征:
练 习:
1.有一个容量为50的样本数据的分组的频数如下:
[12.5, 15.5) 3
[15.5, 18.5) 8
[18.5, 21.5) 9
[21.5, 24.5) 11
[24.5, 27.5) 10
[27.5, 30.5) 5
[30.5, 33.5) 4
(1)列出样本的频率分布表;
(2)画出频率分布直方图;
(3)根据频率分布直方图估计,数据落在[15.5, 24.5)的百分比是多少?
解:组距为3
分组 频数 频率 频率/ 组距
[12.5, 15.5) 3
[15.5, 18.5) 8
[18.5, 21.5) 9
[21.5, 24.5) 11
[24.5, 27.5) 10
[27.5, 30.5) 5
[30.5, 33.5) 4
0.06
0.16
0.18
0.22
0.20
0.10
0.08
0.020
0.053
0.060
0.073
0.067
0.033
0.027
频率分布直方图如下:
频率
组距
0.010
0.020
0.030
0.040
0.050
12.5
15.5
0.060
0.070
练习:2 .投掷一枚均匀骰子44次的记录是:
3 2 4 1 5 1 3 4 5 6 5
4 2 5 3 1 3 4 1 4 5 1
6 3 3 1 2 4 2 6 3 4 6
6 1 6 2 2 5 2 6 5 4 3
现对这些数据进行整理,试画出频数分布直方图.
第一步:写出样本可能出现的一切数值,即:
1,2,3,4,5,6 共6个数.(数据分组)
第二步:列出频率分布表:
样本 1 2 3 4 5 6
频数 7 7 8 8 7 7
频率 0.16 0.16 0.18 0.18 0.16 0.16
组距=1
第三步: 画频率分布直方图
频数 茎 叶
2 10 7, 8
11 11 2, 7, 6, 3, 6, 8, 6, 7, 2, 2,0
13 12 6, 8, 4, 2, 7, 8, 6, 1, 0, 4, 3, 2, 0
4 13 4, 2, 3, 0
下表一组数据是某车间30名工人加工零件的个数, 设计一个
茎叶图表示这组数据,并说明这一车间的生产情况.
134 112 117 126 128 124 122 116 113 107
116 132 127 128 126 121 120 118 108 110
133 130 124 116 117 123 122 120 112 112
练习:
小结:
画频率分布直方图的步骤:
第一步: 求极差: (数据组中最大值与最小值的差距)
第二步: 决定组距与组数: (强调取整)
第三步: 将数据分组 ( 给出组的界限)
第四步: 列频率分布表. (包括分组、频数、频率、频率/组距)
第五步: 画频率分布直方图(在频率分布表的基础上绘制,横坐标为样本数据尺寸,纵坐标为频率/组距.)
组距:指每个小组的两个端点的距离,组距
组数:将数据分组,当数据在100个以内时,
按数据多少常分5-12组。
作业:P71第一题 习题2.2:2
注意
(2)纵坐标为:
再见
