5.5 向心加速度—课件 (共23张PPT)
文档属性
| 名称 | 5.5 向心加速度—课件 (共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 502.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-05-24 14:20:50 | ||
图片预览





文档简介
(共23张PPT)
向心加速度
人教版物理必修二第五章第五节
学习目标:
1.理解向心加速度的概念。
2.知道向心加速度和线速度、角速度的关系式。
3.能够运用向心加速度公式求解有关问题。
匀速圆周运动的实质是什么?
那么做匀速圆周运动的物体所受的合力有何特点?加速度又怎样呢?
匀速圆周运动是变速曲线运动
变速曲线运动
运动状态改变
一定受到外力
一定存在加速度
复习提问
思考讨论
一、感知加速度的方向
想一想:
地球受到什么力的作用?
这个力可能沿什么方向?
感知加速度的方向
应该受到指向太阳的引力作用
一、感知加速度的方向
想一想:小球受到几个力的作用?
这几个力的合力沿什么方向?
感知加速度的方向
一、感知加速度的方向
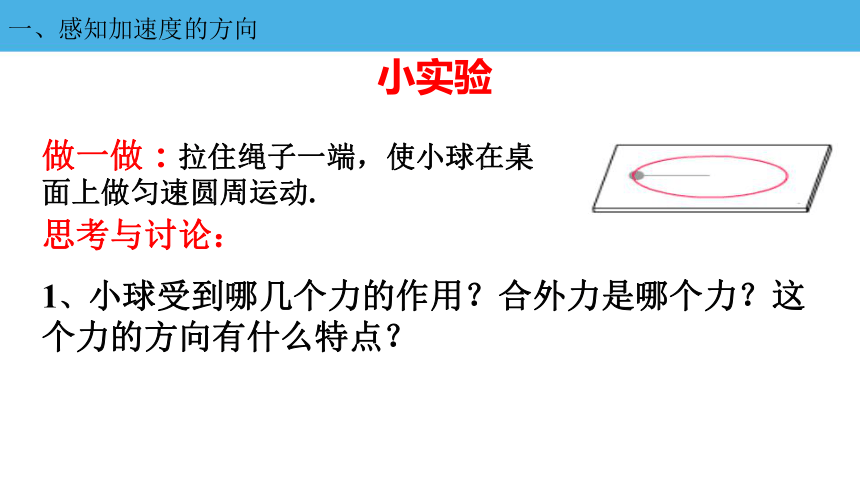
小实验
做一做:拉住绳子一端,使小球在桌面上做匀速圆周运动.
思考与讨论:
1、小球受到哪几个力的作用?合外力是哪个力?这个力的方向有什么特点?
一、感知加速度的方向
O
G
N
F
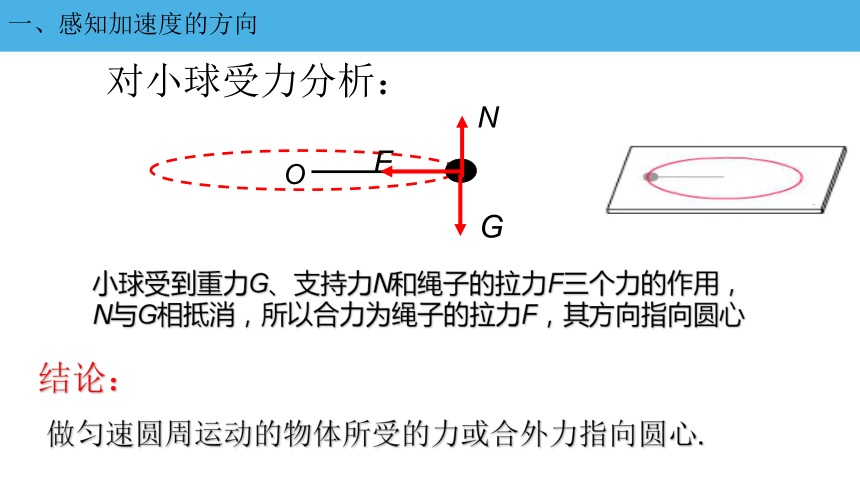
对小球受力分析:
小球受到重力G、支持力N和绳子的拉力F三个力的作用,N与G相抵消,所以合力为绳子的拉力F,其方向指向圆心
结论:
做匀速圆周运动的物体所受的力或合外力指向圆心.
N
一、感知加速度的方向
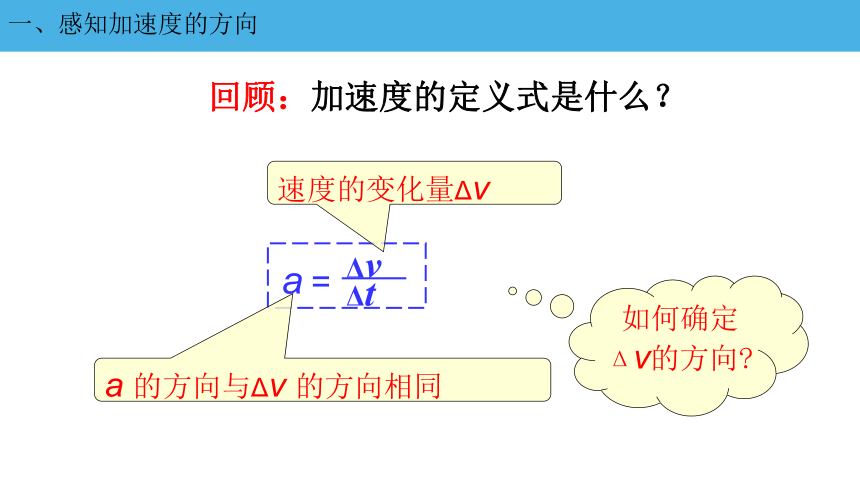
回顾:加速度的定义式是什么?
a =
Δt
Δv
a 的方向与Δv 的方向相同
如何确定Δv的方向?
速度的变化量Δv
一、感知加速度的方向
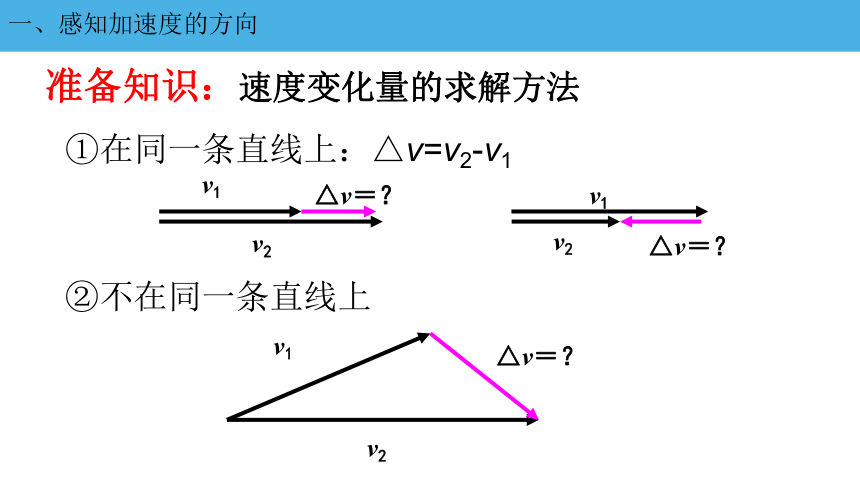
①在同一条直线上:△v=v2-v1
准备知识:速度变化量的求解方法
v1
v2
△v=?
v1
v2
△v=?
v1
v2
△v=?
②不在同一条直线上
一、感知加速度的方向
速度的变化量△v与初速度v1和末速度v2的关系:从同一点作出物体在一段时间的始末两个速度的矢量v1和v 2,从初速度矢量v1的末端作一个矢量△v至末速度矢量v2的末端,矢量△v就等于速度的变化量.
速度的变化量
探究:设质点沿半径为r的圆周运动,某时刻位于A点,速度为vA,经过时间后位于B点,速度为vB,质点速度的变化量沿什么方向?
一、感知加速度的方向
设质点沿半径为r 的圆做匀速圆周运动,某时刻位于A点,速度为vA ,经过时间△t 后位于B点,速度为vB .
vA
Δv
O
A
B
vB
vA
Δv
B
vB
vA
Δv
B
vB
vA
vA
Δv
vB
一、感知加速度的方向
注意:
1、 vA 、vB的长度是否一样?
2、vA平移时注意什么?
3、△v/△t表示什么?
4、△v与圆的半径平行吗?在什么条件下,△v与圆的半径平行?
结论:当△t很小很小时,△v指向圆心.
一、感知加速度的方向
一、感知加速度的方向
一、感知加速度的方向
向心加速度
1、定义:做匀速圆周运动的物体加速度指向圆心,这个加速度称为向心加速度
3、表达式:an=?
指向圆心
设做匀速圆周运动的物体的线速度的大小为v ,轨迹半径为r。经过时间△t,物体从A点运动到B点。尝试用v 、r 写出向心加速度的表达式.
2、方向:时刻变化,始终指向圆心
二、向心加加速度
二、向心加加速度
1、定义:做匀速圆周运动的物体加速度指向圆心,这个加速度称为向心加速度
4、物理意义:描述速度方向变化的快慢
2、符号:an
3、方向:始终指向圆心
5、说明:匀速圆周运动加速度的大小不变,方向时刻改变,所以匀速圆周运动不是匀变速运动,是变加速运动
指向圆心
向心加速度的表达式:
an =
v2
r
an = rω2
an = r
4π2
T 2
从公式 看,向心加速度与半径成反比;从公式 看,向心加速度与半径成正比;这两个结论是否矛盾?
an =
v2
r
an = rω2
v不变时,an与r 成反比
ω不变时,an与r 成正比
二、向心加加速度
思考讨论
下列关于向心加速度的说法中正确的是( )
A.向心加速度表示做圆周运动的物体速率改变的快慢
B.向心加速度的方向不一定指向圆心
C.向心加速度描述线速度方向变化的快慢
D.匀速圆周运动的向心加速度不变
例题
如图所示,一球体绕轴O1O2以角速度ω匀速旋转,A、B为球体表面上两点,下列几种说法中正确的是( )
A.A、B两点具有相同的角速度
B.A、B两点具有相同的线速度
C.A、B两点的向心加速度的方向都指向球心
D.A、B两点的向心加速度大小之比为2∶1
例题
如图所示的皮带传动装置中,甲轮的轴和乙、丙轮的轴均为水平轴,其中,甲、丙两轮半径相等,乙轮半径是丙轮半径的一半.A、B、C三点分别是甲、乙、丙三轮边缘上的点,若传动中皮带不打滑,则( )
A.A、B两点的线速度大小之比为2∶1
B.B、C两点的角速度之比为1∶2
C.A、B两点的向心加速度大小之比为2∶1
D.A、C两点的向心加速度大小之比为1∶4
例题
an =
v2
r
an = rω2
1.定义:匀速圆周运动的加速度
2.意义:描述速度方向变化的快慢
3.大小:
4.方向:始终指向圆心(时刻改变)
匀速圆周运动是变加速运动
向心加速度
小结
作业
同步练习
T
谢谢观看
HANK YOU!
向心加速度
人教版物理必修二第五章第五节
学习目标:
1.理解向心加速度的概念。
2.知道向心加速度和线速度、角速度的关系式。
3.能够运用向心加速度公式求解有关问题。
匀速圆周运动的实质是什么?
那么做匀速圆周运动的物体所受的合力有何特点?加速度又怎样呢?
匀速圆周运动是变速曲线运动
变速曲线运动
运动状态改变
一定受到外力
一定存在加速度
复习提问
思考讨论
一、感知加速度的方向
想一想:
地球受到什么力的作用?
这个力可能沿什么方向?
感知加速度的方向
应该受到指向太阳的引力作用
一、感知加速度的方向
想一想:小球受到几个力的作用?
这几个力的合力沿什么方向?
感知加速度的方向
一、感知加速度的方向
小实验
做一做:拉住绳子一端,使小球在桌面上做匀速圆周运动.
思考与讨论:
1、小球受到哪几个力的作用?合外力是哪个力?这个力的方向有什么特点?
一、感知加速度的方向
O
G
N
F
对小球受力分析:
小球受到重力G、支持力N和绳子的拉力F三个力的作用,N与G相抵消,所以合力为绳子的拉力F,其方向指向圆心
结论:
做匀速圆周运动的物体所受的力或合外力指向圆心.
N
一、感知加速度的方向
回顾:加速度的定义式是什么?
a =
Δt
Δv
a 的方向与Δv 的方向相同
如何确定Δv的方向?
速度的变化量Δv
一、感知加速度的方向
①在同一条直线上:△v=v2-v1
准备知识:速度变化量的求解方法
v1
v2
△v=?
v1
v2
△v=?
v1
v2
△v=?
②不在同一条直线上
一、感知加速度的方向
速度的变化量△v与初速度v1和末速度v2的关系:从同一点作出物体在一段时间的始末两个速度的矢量v1和v 2,从初速度矢量v1的末端作一个矢量△v至末速度矢量v2的末端,矢量△v就等于速度的变化量.
速度的变化量
探究:设质点沿半径为r的圆周运动,某时刻位于A点,速度为vA,经过时间后位于B点,速度为vB,质点速度的变化量沿什么方向?
一、感知加速度的方向
设质点沿半径为r 的圆做匀速圆周运动,某时刻位于A点,速度为vA ,经过时间△t 后位于B点,速度为vB .
vA
Δv
O
A
B
vB
vA
Δv
B
vB
vA
Δv
B
vB
vA
vA
Δv
vB
一、感知加速度的方向
注意:
1、 vA 、vB的长度是否一样?
2、vA平移时注意什么?
3、△v/△t表示什么?
4、△v与圆的半径平行吗?在什么条件下,△v与圆的半径平行?
结论:当△t很小很小时,△v指向圆心.
一、感知加速度的方向
一、感知加速度的方向
一、感知加速度的方向
向心加速度
1、定义:做匀速圆周运动的物体加速度指向圆心,这个加速度称为向心加速度
3、表达式:an=?
指向圆心
设做匀速圆周运动的物体的线速度的大小为v ,轨迹半径为r。经过时间△t,物体从A点运动到B点。尝试用v 、r 写出向心加速度的表达式.
2、方向:时刻变化,始终指向圆心
二、向心加加速度
二、向心加加速度
1、定义:做匀速圆周运动的物体加速度指向圆心,这个加速度称为向心加速度
4、物理意义:描述速度方向变化的快慢
2、符号:an
3、方向:始终指向圆心
5、说明:匀速圆周运动加速度的大小不变,方向时刻改变,所以匀速圆周运动不是匀变速运动,是变加速运动
指向圆心
向心加速度的表达式:
an =
v2
r
an = rω2
an = r
4π2
T 2
从公式 看,向心加速度与半径成反比;从公式 看,向心加速度与半径成正比;这两个结论是否矛盾?
an =
v2
r
an = rω2
v不变时,an与r 成反比
ω不变时,an与r 成正比
二、向心加加速度
思考讨论
下列关于向心加速度的说法中正确的是( )
A.向心加速度表示做圆周运动的物体速率改变的快慢
B.向心加速度的方向不一定指向圆心
C.向心加速度描述线速度方向变化的快慢
D.匀速圆周运动的向心加速度不变
例题
如图所示,一球体绕轴O1O2以角速度ω匀速旋转,A、B为球体表面上两点,下列几种说法中正确的是( )
A.A、B两点具有相同的角速度
B.A、B两点具有相同的线速度
C.A、B两点的向心加速度的方向都指向球心
D.A、B两点的向心加速度大小之比为2∶1
例题
如图所示的皮带传动装置中,甲轮的轴和乙、丙轮的轴均为水平轴,其中,甲、丙两轮半径相等,乙轮半径是丙轮半径的一半.A、B、C三点分别是甲、乙、丙三轮边缘上的点,若传动中皮带不打滑,则( )
A.A、B两点的线速度大小之比为2∶1
B.B、C两点的角速度之比为1∶2
C.A、B两点的向心加速度大小之比为2∶1
D.A、C两点的向心加速度大小之比为1∶4
例题
an =
v2
r
an = rω2
1.定义:匀速圆周运动的加速度
2.意义:描述速度方向变化的快慢
3.大小:
4.方向:始终指向圆心(时刻改变)
匀速圆周运动是变加速运动
向心加速度
小结
作业
同步练习
T
谢谢观看
HANK YOU!
