10.3 平行线的性质(要点测评+课后集训+答案)
文档属性
| 名称 | 10.3 平行线的性质(要点测评+课后集训+答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-24 17:36:32 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
沪科版数学七年级下册同步课时训练
第10章 相交线、平行线与平移
10.3 平行线的性质
要点测评 基础达标
要点1 平行线的性质
1. 如图,直线EF分别交AB,CD于点E,F,且AB∥CD,若∠1=60°,则∠2= .?
2. 如图所示,已知AD∥BC,AB∥DC,求证:∠A=∠C.
要点2 平行线的判定与性质的综合应用
3. 已知三角形ABC中,∠B=70°,CD平分∠ACB,∠2=∠3,求∠1的度数.
4. 已知:如图所示,DE∥AB,∠1=∠A,求证:DF∥AC.
要点3 平行线的判定与性质的实际应用
5. 如图所示,要在一条公路的两侧铺设平行管道,已知一侧铺设的角度为120°,为使管道对接,另一侧铺设的角度大小应为( )
A. 120° B. 100° C. 80° D. 60°
6. 如图所示,潜望镜中的两个镜子是互相平行放置的,光线经过镜子反射时,∠1=∠2,∠3=∠4,请解释为什么进入潜望镜的光线和离开潜望镜的光线是平行的?
课后集训 巩固提升
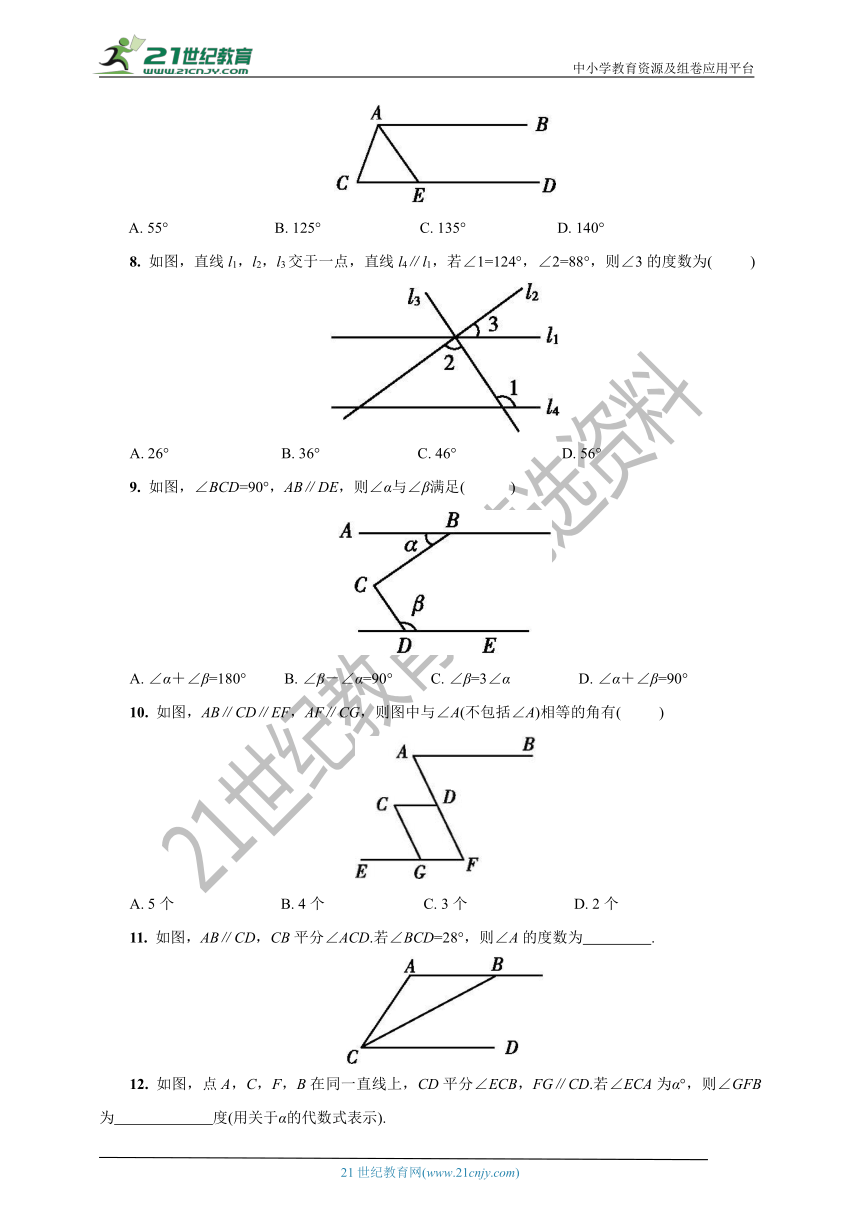
7. 如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=70°,则∠AED等于( )
A. 55° B. 125° C. 135° D. 140°
8. 如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=124°,∠2=88°,则∠3的度数为( )
A. 26° B. 36° C. 46° D. 56°
9. 如图,∠BCD=90°,AB∥DE,则∠α与∠β满足( )
A. ∠α+∠β=180° B. ∠β-∠α=90° C. ∠β=3∠α D. ∠α+∠β=90°
10. 如图,AB∥CD∥EF,AF∥CG,则图中与∠A(不包括∠A)相等的角有( )
A. 5个 B. 4个 C. 3个 D. 2个
11. 如图,AB∥CD,CB平分∠ACD.若∠BCD=28°,则∠A的度数为 .?
12. 如图,点A,C,F,B在同一直线上,CD平分∠ECB,FG∥CD.若∠ECA为α°,则∠GFB为 度(用关于α的代数式表示).?
13. 一大门的栏杆如图所示,BA垂直地面AE于A,CD平行于地面AE,若∠BCD=150°,则∠ABC的度数为 .?
14. 阅读理解并填空.
如图,已知AB∥CD,∠1=∠2,试证明EP∥FQ.
证明:因为AB∥CD,
所以∠MEB=∠MFD( )?
又因为∠1=∠2,
所以∠MEB-∠1=∠MFD-∠ ,?
即∠MEP=∠ .?
所以EP∥ ( ).?
15. 如图所示,已知∠B=43°,∠BDC=43°,∠A=∠1,证明:∠4=∠BDE.
16. 如图所示,已知,AB∥CD,分别探讨四个图形中∠APC,∠PAB,∠PCD的关系.
(1)请说明图①,图②中三个角的关系,并任选一个加以证明.
(2)猜想图③,图④中三个角的关系,不必说明理由.
参 考 答 案
1. 120°
2. 证明:因为AD∥BC,AB∥DC,所以∠A+∠B=180°,∠C+∠B=180°,所以∠A=180-∠B,∠C=180-∠B,所以∠A=∠C.
3. 解:CD平分∠ACB,所以∠3=∠DCB(角平分线定义). 因为∠2=∠3(已知),所以∠2=∠DCB(等量代换). 所以DE∥BC(内错角相等,两直线平行),所以∠1=∠B=70°(两直线平行,同位角相等).
4. 证明:因为DE∥AB,所以∠A+∠AED=180°(两直线平行,同旁内角互补). 因为∠1=∠A(已知),所以∠1+∠AED=180°(等量代换). 所以DF∥AC(同旁内角互补,两直线平行).
5. D
6. 解:由两面镜子是相互平行的,得∠2=∠3(两直线平行,内错角相等). 由∠1=∠2,∠3=∠4,得∠1=∠2=∠3=∠4. 因为∠5=180°-∠1-∠2,∠6=180°-∠3-∠4,所以∠5=∠6. 因为∠5与∠6是内错角,所以两条光线是互相平行的.
7. B 8. B 9. B 10. B
11. 124°
12. 90-
13. 120°
14. 证明:因为AB∥CD,所以∠MEB=∠MFD( 两直线平行,同位角相等 )? 又因为∠1=∠2,所以∠MEB-∠1=∠MFD-∠ 2 ,?即∠MEP=∠ MFQ .? 所以EP∥ FQ ( 同位角相等,两直线平行 ).?
15. 证明:因为∠B=43°,∠BDC=43°(已知),所以∠B=∠BDC(等量代换). 所以AB∥CD(内错角相等,两直线平行). 所以∠A=∠C(两直线平行,内错角相等). 因为∠A=∠1(已知),所以∠C=∠1(等量代换). 所以AC∥DE(内错角相等,两直线平行). 所以∠4=∠BDE(两直线平行,内错角相等).
16. 解:(1)题图①,∠PAB+∠APC+∠PCD=360°,
题图②,∠PAB+∠PCD=∠APC,
证明题图①:过P作PE∥AB,所以∠PAB+∠APE=180°,又因为AB∥CD,所以CD∥PE,所以∠PCD+∠CPE=180°,所以∠PAB+∠APE+∠EPC+∠PCD=360°,即∠PAB+∠APC+∠PCD=360°.
(2)题图③∠PCD=∠PAB+∠APC,题图④∠PAB=∠PCD+∠APC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
沪科版数学七年级下册同步课时训练
第10章 相交线、平行线与平移
10.3 平行线的性质
要点测评 基础达标
要点1 平行线的性质
1. 如图,直线EF分别交AB,CD于点E,F,且AB∥CD,若∠1=60°,则∠2= .?
2. 如图所示,已知AD∥BC,AB∥DC,求证:∠A=∠C.
要点2 平行线的判定与性质的综合应用
3. 已知三角形ABC中,∠B=70°,CD平分∠ACB,∠2=∠3,求∠1的度数.
4. 已知:如图所示,DE∥AB,∠1=∠A,求证:DF∥AC.
要点3 平行线的判定与性质的实际应用
5. 如图所示,要在一条公路的两侧铺设平行管道,已知一侧铺设的角度为120°,为使管道对接,另一侧铺设的角度大小应为( )
A. 120° B. 100° C. 80° D. 60°
6. 如图所示,潜望镜中的两个镜子是互相平行放置的,光线经过镜子反射时,∠1=∠2,∠3=∠4,请解释为什么进入潜望镜的光线和离开潜望镜的光线是平行的?
课后集训 巩固提升
7. 如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=70°,则∠AED等于( )
A. 55° B. 125° C. 135° D. 140°
8. 如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=124°,∠2=88°,则∠3的度数为( )
A. 26° B. 36° C. 46° D. 56°
9. 如图,∠BCD=90°,AB∥DE,则∠α与∠β满足( )
A. ∠α+∠β=180° B. ∠β-∠α=90° C. ∠β=3∠α D. ∠α+∠β=90°
10. 如图,AB∥CD∥EF,AF∥CG,则图中与∠A(不包括∠A)相等的角有( )
A. 5个 B. 4个 C. 3个 D. 2个
11. 如图,AB∥CD,CB平分∠ACD.若∠BCD=28°,则∠A的度数为 .?
12. 如图,点A,C,F,B在同一直线上,CD平分∠ECB,FG∥CD.若∠ECA为α°,则∠GFB为 度(用关于α的代数式表示).?
13. 一大门的栏杆如图所示,BA垂直地面AE于A,CD平行于地面AE,若∠BCD=150°,则∠ABC的度数为 .?
14. 阅读理解并填空.
如图,已知AB∥CD,∠1=∠2,试证明EP∥FQ.
证明:因为AB∥CD,
所以∠MEB=∠MFD( )?
又因为∠1=∠2,
所以∠MEB-∠1=∠MFD-∠ ,?
即∠MEP=∠ .?
所以EP∥ ( ).?
15. 如图所示,已知∠B=43°,∠BDC=43°,∠A=∠1,证明:∠4=∠BDE.
16. 如图所示,已知,AB∥CD,分别探讨四个图形中∠APC,∠PAB,∠PCD的关系.
(1)请说明图①,图②中三个角的关系,并任选一个加以证明.
(2)猜想图③,图④中三个角的关系,不必说明理由.
参 考 答 案
1. 120°
2. 证明:因为AD∥BC,AB∥DC,所以∠A+∠B=180°,∠C+∠B=180°,所以∠A=180-∠B,∠C=180-∠B,所以∠A=∠C.
3. 解:CD平分∠ACB,所以∠3=∠DCB(角平分线定义). 因为∠2=∠3(已知),所以∠2=∠DCB(等量代换). 所以DE∥BC(内错角相等,两直线平行),所以∠1=∠B=70°(两直线平行,同位角相等).
4. 证明:因为DE∥AB,所以∠A+∠AED=180°(两直线平行,同旁内角互补). 因为∠1=∠A(已知),所以∠1+∠AED=180°(等量代换). 所以DF∥AC(同旁内角互补,两直线平行).
5. D
6. 解:由两面镜子是相互平行的,得∠2=∠3(两直线平行,内错角相等). 由∠1=∠2,∠3=∠4,得∠1=∠2=∠3=∠4. 因为∠5=180°-∠1-∠2,∠6=180°-∠3-∠4,所以∠5=∠6. 因为∠5与∠6是内错角,所以两条光线是互相平行的.
7. B 8. B 9. B 10. B
11. 124°
12. 90-
13. 120°
14. 证明:因为AB∥CD,所以∠MEB=∠MFD( 两直线平行,同位角相等 )? 又因为∠1=∠2,所以∠MEB-∠1=∠MFD-∠ 2 ,?即∠MEP=∠ MFQ .? 所以EP∥ FQ ( 同位角相等,两直线平行 ).?
15. 证明:因为∠B=43°,∠BDC=43°(已知),所以∠B=∠BDC(等量代换). 所以AB∥CD(内错角相等,两直线平行). 所以∠A=∠C(两直线平行,内错角相等). 因为∠A=∠1(已知),所以∠C=∠1(等量代换). 所以AC∥DE(内错角相等,两直线平行). 所以∠4=∠BDE(两直线平行,内错角相等).
16. 解:(1)题图①,∠PAB+∠APC+∠PCD=360°,
题图②,∠PAB+∠PCD=∠APC,
证明题图①:过P作PE∥AB,所以∠PAB+∠APE=180°,又因为AB∥CD,所以CD∥PE,所以∠PCD+∠CPE=180°,所以∠PAB+∠APE+∠EPC+∠PCD=360°,即∠PAB+∠APC+∠PCD=360°.
(2)题图③∠PCD=∠PAB+∠APC,题图④∠PAB=∠PCD+∠APC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
