人教版七年级下册数学课件:6.3 实数的概念(共45张PPT)
文档属性
| 名称 | 人教版七年级下册数学课件:6.3 实数的概念(共45张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-24 00:00:00 | ||
图片预览










文档简介
(共45张PPT)
初一年级 数学
实数的概念
是不是有理数呢?
思考:
整数和分数
复习回顾
无限不循环小数
1.414 213 562 373…
请把下列分数写成小数形式,你有什么发现?
探究活动
, , , , , .
分数都能写成有限小数或无限循环小数形式.
解决问题
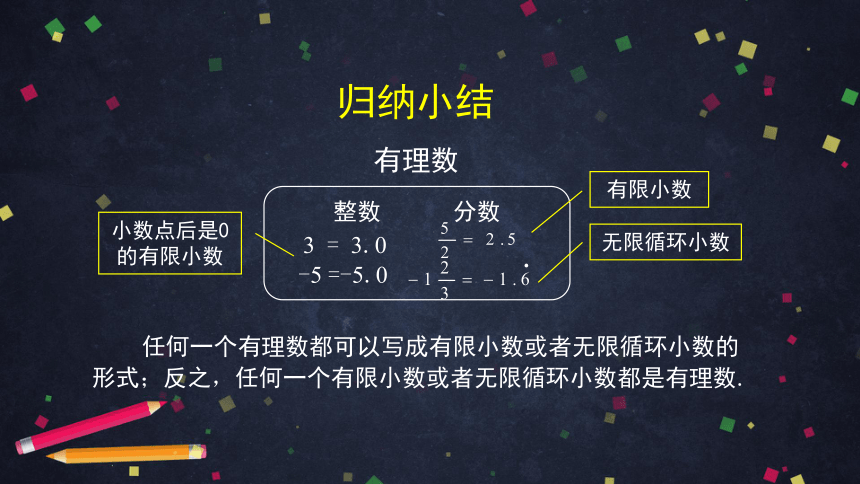
整数 分数
3 = 3.0
-5 =-5.0
无限循环小数
小数点后是0的有限小数
有理数
有限小数
归纳小结
任何一个有理数都可以写成有限小数或者无限循环小数的形式;反之,任何一个有限小数或者无限循环小数都是有理数.
是无限不循环小数,
既不属于整数也不属于分数,
所以它不是有理数.
归纳小结
继续思考: 到底是什么数呢?
有理数
无理数
3=3.0 -5=-5.0
有限小数
无限循环小数
无限不循环小数
你还能再举出一些无限不循环小数的例子吗?
1.414 213 562…
1.732 050 807…
1.709 975 946…
3.141 592 653…
π
探究新知
无理数的概念:无限不循环的小数叫做无理数.
无理数特点
① 是小数;
② 是无限小数;
③ 是不循环的无限小数.
探究新知
π
都是无理数,
无理数的个数有无限多个.
, , , , .
π
例题 判断下列这组数中,哪些是无理数?
典型例题
根据 ,算出 ,
这还是个无限不循环小数,所以它是无理数.
分析过程:
π
根据 ,算出 ,
这还是个无限不循环小数,所以它是无理数.
π
π
,
无理数
无限循环小数
有理数
有限小数
有理数
分析过程:
分析思路:
判断数的类型
依据无理数、有理数的概念.
所以 这三个数是无理数.
π
例题 已知数0.101001000100001…,它的特点是从左向右看,相邻的两个1之间依次多一个0,这个数是有理数还是无理数,为什么?
试一试你还能写出类似这样的数吗?
典型例题
思路:
依据无理数概念.
2.212112111211112…
典型例题
例题 判断正误,并说明理由.
③ 带根号的数都是无理数.
① 无理数都是无限小数;
② 无限小数都是无理数;
典型例题
例题 判断正误,并说明理由.
① 无理数都是无限小数;
所以这句话正确
无限不循环小数
无限不循环小数
无限循环小数
无限小数
② 无限小数都是无理数;
这句话是错误的.
③ 带根号的数都是无理数.
这句话是错误的.
无理数
有理数
分析思路:
判断命题真假
依据概念
反例: .
实数的概念:无理数与有理数统称实数.
再探新知
无限循环小数
有限小数
有理数
无理数
无限不循环小数
现实世界中客观存在的量的反映
正无理数
负无理数
正有理数
负有理数
0
有限小数或无限循环小数
无限不循环小数
有理数
无理数
实数
思考:实数可以怎样分类呢?
整数
分数
有理数
类比
再探新知
再探新知
思考:因为非零有理数和无理数都有正负之分,那么你还
能类比有理数的分类方法,按大小关系对实数重新分类吗?
0
正实数
负实数
实数
负有理数
负无理数
正有理数
正无理数
正无理数
负无理数
正有理数
负有理数
0
有理数
无理数
实数
对比
分类标准
例题 判断正误,并说明理由.
① 是无理数;
② 0 既不是有理数也不是无理数.
典型例题
判断依据
实数概念及分类
① 是无理数;
错误
分析过程:
因为 是无限循环小数,所以它不是无理数.
还可以根据实数的分类直接判断 是分数,属于有理数.
错误
分析过程:
② 0 既不是有理数也不是无理数.
有理数
无理数
实数
正有理数
负有理数
0
例题 在 0.2020020002…
(相邻的两个2之间依次多一个0)这五个数中,既是正实数也是无理数的数有( ).
典型例题
(A)1个
(B)2个
(C)3个
(D)4个
0.2020020002….
正实数
有理数
不符题意
负实数
无理数
不符题意
负实数
有理数
不符题意
正实数
有理数
不符题意
正实数
无理数
符合题意
例题 在 0.2020020002…
(相邻的两个2之间依次多一个0)这五个数中,既是正实数也是无理数的数有( ).
典型例题
(A)1个
(B)2个
(C)3个
(D)4个
A
例题 把下列各数分别填到相应的集合中:
…
无理数集合
有理数集合
…
典型例题
π
=3
有理数
无限循环小数
有理数
有限小数
有理数
整数
有理数
分数
有理数
无理数
无理数
=2
有理数
无理数
π
无理数集合
有理数集合
…
π
…
例题 有一个数值转换器,操作如下图所示,则当输入的 x 为 81 时,输出的 y 是 ( ).
典型例题
(A)
(B)
(D)
(C)
输入 x ( x > 0 )
是无理数
输出 y
是有理数
操作过程:
输入:3
是无理数
输出
第三步
输入:81
9是有理数
第一步
=9
输入:9
3是有理数
第二步
=3
例题 有一个数值转换器,操作如下图所示,则当输入的 x 为 81 时,输出的 y 是 ( ).
典型例题
(A)
(B)
(D)
(C)
输入 x ( x > 0 )
是无理数
输出 y
是有理数
B
拓展材料
希帕索斯
(毕达哥拉斯学派的年轻数学家)
发现第一个无理数
从有理数到实数,是数的范围的一次重要扩充.
1. 下列各数中的无理数是( ).
(A)
(B)
(C)
D
=5
有理数
有限小数
有理数
分数
有理数
无理数
巩固练习
(D)
π
①实数包括正实数、0、负实数;
②无理数包括正无理数、0、负无理数;
③不带根号的数都是有理数.
错误
正确
2. 判断正误,并说明理由.
巩固练习
反例:0.1010010001…
错误
3. 把下列各数填入相应的集合内:
①无理数集合:{ };②有理数集合:{ };
③负实数集合:{ };④正实数集合:{ }.
巩固练习
π
①无理数集合:{ };
②有理数集合:{ };
巩固练习
π
π
π
③负实数集合:{ };
④正实数集合:{ }.
巩固练习
π
4. 在下列每个圈里,至少填入三个适当的数.
…
无理数集合
有理数集合
…
巩固练习
π
5.有一个数值转换器,操作如下图所示,则当输入的
x 为 64 时,输出的数值是__________.
巩固练习
输入 x
是无理数
输出
是有理数
输入: 64
是有理数
4
操作过程:
第一步
第二步
输入: 4
是无理数,输出数值
5.有一个数值转换器,操作如下图所示,则当输入的
x 为 64 时,输出的数值是__________.
巩固练习
输入 x
是无理数
输出
是有理数
6.在实数0,1,2,3,4,5,6,7,8,9的平方根及立方根中,哪些是有理数?哪些是无理数?
0 1 2 3 4 5 6 7 8 9
平方根
立方根
巩固练习
先列表整理,再观察求值,然后判断类型.
1.了解无理数和实数的概念,梳理本节课的学习思路;
课堂小结
无理数的概念
类比
有理数分类
实数的分类
探究活动
归纳新知
思考 是什么数
扩充数系
实数的概念
2.了解实数的分类,会在实数范围内对数分类整理.
把下列各数分别填到相应的集合中:
…
无理数集合
有理数集合
课后作业
1. 书上57页习题6.3复习巩固第2题;
π
…
2. 阅读书上58页《为什么说 不是有理数》.
课后作业
同学们再见!
初一年级 数学
实数的概念
是不是有理数呢?
思考:
整数和分数
复习回顾
无限不循环小数
1.414 213 562 373…
请把下列分数写成小数形式,你有什么发现?
探究活动
, , , , , .
分数都能写成有限小数或无限循环小数形式.
解决问题
整数 分数
3 = 3.0
-5 =-5.0
无限循环小数
小数点后是0的有限小数
有理数
有限小数
归纳小结
任何一个有理数都可以写成有限小数或者无限循环小数的形式;反之,任何一个有限小数或者无限循环小数都是有理数.
是无限不循环小数,
既不属于整数也不属于分数,
所以它不是有理数.
归纳小结
继续思考: 到底是什么数呢?
有理数
无理数
3=3.0 -5=-5.0
有限小数
无限循环小数
无限不循环小数
你还能再举出一些无限不循环小数的例子吗?
1.414 213 562…
1.732 050 807…
1.709 975 946…
3.141 592 653…
π
探究新知
无理数的概念:无限不循环的小数叫做无理数.
无理数特点
① 是小数;
② 是无限小数;
③ 是不循环的无限小数.
探究新知
π
都是无理数,
无理数的个数有无限多个.
, , , , .
π
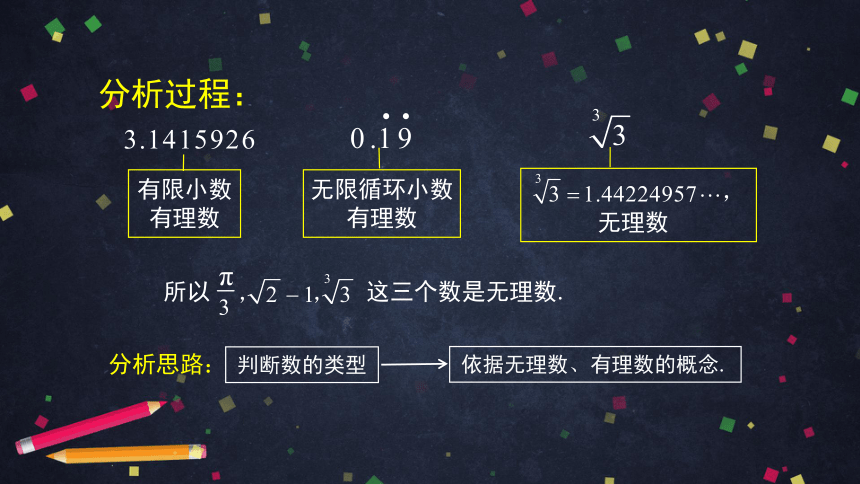
例题 判断下列这组数中,哪些是无理数?
典型例题
根据 ,算出 ,
这还是个无限不循环小数,所以它是无理数.
分析过程:
π
根据 ,算出 ,
这还是个无限不循环小数,所以它是无理数.
π
π
,
无理数
无限循环小数
有理数
有限小数
有理数
分析过程:
分析思路:
判断数的类型
依据无理数、有理数的概念.
所以 这三个数是无理数.
π
例题 已知数0.101001000100001…,它的特点是从左向右看,相邻的两个1之间依次多一个0,这个数是有理数还是无理数,为什么?
试一试你还能写出类似这样的数吗?
典型例题
思路:
依据无理数概念.
2.212112111211112…
典型例题
例题 判断正误,并说明理由.
③ 带根号的数都是无理数.
① 无理数都是无限小数;
② 无限小数都是无理数;
典型例题
例题 判断正误,并说明理由.
① 无理数都是无限小数;
所以这句话正确
无限不循环小数
无限不循环小数
无限循环小数
无限小数
② 无限小数都是无理数;
这句话是错误的.
③ 带根号的数都是无理数.
这句话是错误的.
无理数
有理数
分析思路:
判断命题真假
依据概念
反例: .
实数的概念:无理数与有理数统称实数.
再探新知
无限循环小数
有限小数
有理数
无理数
无限不循环小数
现实世界中客观存在的量的反映
正无理数
负无理数
正有理数
负有理数
0
有限小数或无限循环小数
无限不循环小数
有理数
无理数
实数
思考:实数可以怎样分类呢?
整数
分数
有理数
类比
再探新知
再探新知
思考:因为非零有理数和无理数都有正负之分,那么你还
能类比有理数的分类方法,按大小关系对实数重新分类吗?
0
正实数
负实数
实数
负有理数
负无理数
正有理数
正无理数
正无理数
负无理数
正有理数
负有理数
0
有理数
无理数
实数
对比
分类标准
例题 判断正误,并说明理由.
① 是无理数;
② 0 既不是有理数也不是无理数.
典型例题
判断依据
实数概念及分类
① 是无理数;
错误
分析过程:
因为 是无限循环小数,所以它不是无理数.
还可以根据实数的分类直接判断 是分数,属于有理数.
错误
分析过程:
② 0 既不是有理数也不是无理数.
有理数
无理数
实数
正有理数
负有理数
0
例题 在 0.2020020002…
(相邻的两个2之间依次多一个0)这五个数中,既是正实数也是无理数的数有( ).
典型例题
(A)1个
(B)2个
(C)3个
(D)4个
0.2020020002….
正实数
有理数
不符题意
负实数
无理数
不符题意
负实数
有理数
不符题意
正实数
有理数
不符题意
正实数
无理数
符合题意
例题 在 0.2020020002…
(相邻的两个2之间依次多一个0)这五个数中,既是正实数也是无理数的数有( ).
典型例题
(A)1个
(B)2个
(C)3个
(D)4个
A
例题 把下列各数分别填到相应的集合中:
…
无理数集合
有理数集合
…
典型例题
π
=3
有理数
无限循环小数
有理数
有限小数
有理数
整数
有理数
分数
有理数
无理数
无理数
=2
有理数
无理数
π
无理数集合
有理数集合
…
π
…
例题 有一个数值转换器,操作如下图所示,则当输入的 x 为 81 时,输出的 y 是 ( ).
典型例题
(A)
(B)
(D)
(C)
输入 x ( x > 0 )
是无理数
输出 y
是有理数
操作过程:
输入:3
是无理数
输出
第三步
输入:81
9是有理数
第一步
=9
输入:9
3是有理数
第二步
=3
例题 有一个数值转换器,操作如下图所示,则当输入的 x 为 81 时,输出的 y 是 ( ).
典型例题
(A)
(B)
(D)
(C)
输入 x ( x > 0 )
是无理数
输出 y
是有理数
B
拓展材料
希帕索斯
(毕达哥拉斯学派的年轻数学家)
发现第一个无理数
从有理数到实数,是数的范围的一次重要扩充.
1. 下列各数中的无理数是( ).
(A)
(B)
(C)
D
=5
有理数
有限小数
有理数
分数
有理数
无理数
巩固练习
(D)
π
①实数包括正实数、0、负实数;
②无理数包括正无理数、0、负无理数;
③不带根号的数都是有理数.
错误
正确
2. 判断正误,并说明理由.
巩固练习
反例:0.1010010001…
错误
3. 把下列各数填入相应的集合内:
①无理数集合:{ };②有理数集合:{ };
③负实数集合:{ };④正实数集合:{ }.
巩固练习
π
①无理数集合:{ };
②有理数集合:{ };
巩固练习
π
π
π
③负实数集合:{ };
④正实数集合:{ }.
巩固练习
π
4. 在下列每个圈里,至少填入三个适当的数.
…
无理数集合
有理数集合
…
巩固练习
π
5.有一个数值转换器,操作如下图所示,则当输入的
x 为 64 时,输出的数值是__________.
巩固练习
输入 x
是无理数
输出
是有理数
输入: 64
是有理数
4
操作过程:
第一步
第二步
输入: 4
是无理数,输出数值
5.有一个数值转换器,操作如下图所示,则当输入的
x 为 64 时,输出的数值是__________.
巩固练习
输入 x
是无理数
输出
是有理数
6.在实数0,1,2,3,4,5,6,7,8,9的平方根及立方根中,哪些是有理数?哪些是无理数?
0 1 2 3 4 5 6 7 8 9
平方根
立方根
巩固练习
先列表整理,再观察求值,然后判断类型.
1.了解无理数和实数的概念,梳理本节课的学习思路;
课堂小结
无理数的概念
类比
有理数分类
实数的分类
探究活动
归纳新知
思考 是什么数
扩充数系
实数的概念
2.了解实数的分类,会在实数范围内对数分类整理.
把下列各数分别填到相应的集合中:
…
无理数集合
有理数集合
课后作业
1. 书上57页习题6.3复习巩固第2题;
π
…
2. 阅读书上58页《为什么说 不是有理数》.
课后作业
同学们再见!
