人教版八年级下册数学18.1.2平行四边形判定定理的简单应用课件 (共18张PPT)
文档属性
| 名称 | 人教版八年级下册数学18.1.2平行四边形判定定理的简单应用课件 (共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-25 10:08:11 | ||
图片预览





文档简介
(共18张PPT)
18.1.3平行四边形判定定理的简单应用
Ⅰ教学目标:
1)进一步理解和掌握平行四边形的判定
2)灵活运用平行四边形判定解决实际问题
Ⅱ教学重难点:
重点是:平行四边形的运用
难点是:平行四边形的灵活运用
教学过程设计
(一)复习知识,形成简约的知识结构
问题 (1)平行四边形的判定定理分别是从哪些方面得到的?
研究顺序:定义-边-角-对角线
(2)请说说这些平行四边形的判定定理。
1.两组对边分别相等的四边形是平行四边形
2.两组对角分别相等的四边形是平行四边形
3.对角线互相平分的四边形是平行四边形
4.一组对边既平行又相等的四边形是平行四边形
5.两组对边分别平行的四边形是平行四边形?
边 角 对角线
平行四边形
(3)你能选择恰当的角度对平行四边形的判定定理进行分类吗?(请用表格呈现)
1)两组对边分别平行的四边形是平行四边形(定义)
?2)两组对边分别相等的四边形是平行四边形?
3)一组对边既平行又相等的四边形是平行四边形?
两组对角分别相等的四边形是平行四边形
对角线互相平分
的四边形是平行四边形
追问:1)判定平行四边形的条件有几个?
2)一组对边平行,另一组对边相等的四边形是平行四边形吗?
2个
等腰梯形
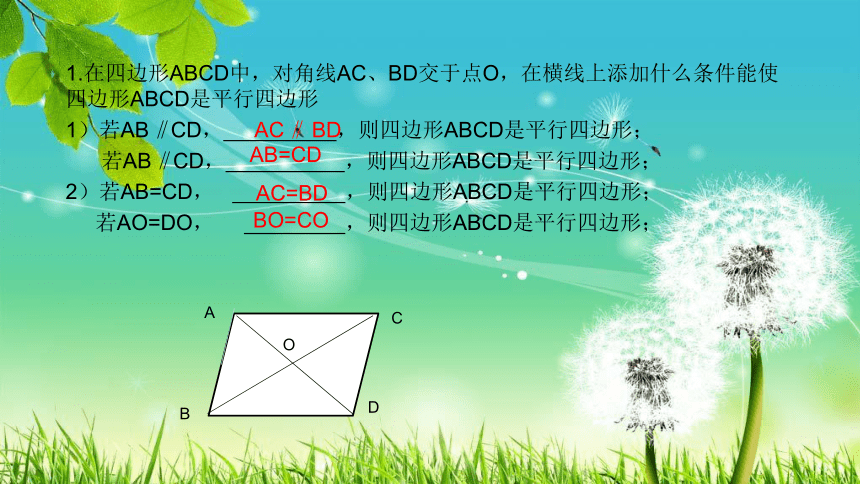
1.在四边形ABCD中,对角线AC、BD交于点O,在横线上添加什么条件能使四边形ABCD是平行四边形
1)若AB‖CD, ,则四边形ABCD是平行四边形;
若AB‖CD, ,则四边形ABCD是平行四边形;
2)若AB=CD, ,则四边形ABCD是平行四边形;
若AO=DO, ,则四边形ABCD是平行四边形;
O
A
B
C
D
AC‖ BD
AB=CD
AC=BD
BO=CO
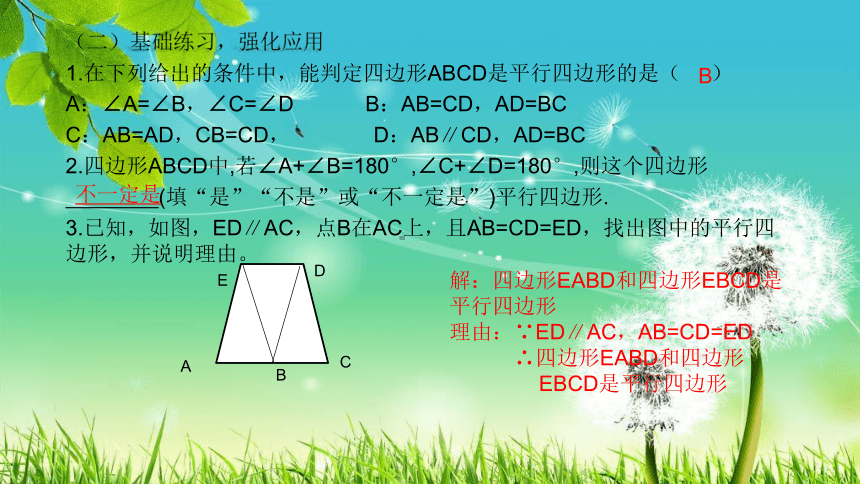
(二)基础练习,强化应用
1.在下列给出的条件中,能判定四边形ABCD是平行四边形的是( )
A:∠A=∠B,∠C=∠D B:AB=CD,AD=BC
C:AB=AD,CB=CD, D:AB∥CD,AD=BC
2.四边形ABCD中,若∠A+∠B=180°,∠C+∠D=180°,则这个四边形
(填“是”“不是”或“不一定是”)平行四边形.?
3.已知,如图,ED∥AC,点B在AC上,且AB=CD=ED,找出图中的平行四边形,并说明理由。
E
A
B
C
D
B
解:四边形EABD和四边形EBCD是平行四边形
理由:∵ED∥AC,AB=CD=ED
∴四边形EABD和四边形
EBCD是平行四边形
不一定是
4.顺次连接四边形各边中点能得到 形.
D
A
B
E
C
F
G
H
证明:依题意,如图示,在四边形ABCD中,点E,F,G,H分别是边AB,BC,CD,DA上的中点,连接点E,F,G,H,试证明四边形EFGH为平行四边形
连接AC
∵点E,F,G,H分别是边AB,BC,CD,DA上的中点
∴EF∥AC,HG∥AC
EF= 1/2 AC ,HG= 1/2 AC
∴EF∥GH且EF=GH
∴四边形EFGH为平行四边形
平行四边
(三)典例引领,深化应用
例1 已知:如图,E,F是平行四边形ABCD对角线上的两点,AE=CF。求证:四边形DEBF是平行四边形。
D
A
B
C
E
F
证明:∵四边形ABCD是平行四边形
∴AD=CB,∠DAE=∠BCF
∵AE=CF
∴△ADE≌△CBF
∴DE=BF ∠AED=∠CFB
∴∠DEF=∠BFE
∴DE∥BF
因此四边形DEBF是平行四边形
追问1:还有其他方法吗?
A
D
C
B
E
F
O
证明:连接BD,交AC于点O
∵四边形ABCD是平行四边形
∴AO=CO,BO=DO
∵AE=CF
∴EO=FO
∴四边形DEBF是平行四边形
变式1:若将题目条件AE=CF改为DE⊥AC,BF⊥AC,其他条件不变,四边形DEBF还是平行四边形吗?并证明(是平行四边形)
C
D
A
B
E
F
∟
∟
证明:∵四边形ABCD是平行四边形
∴AD=CB ,∠DAE=∠BCF
∵DE⊥AC,BF⊥AC,
∴∠DEF=∠BFE,DE∥BF
∴△ADE≌△BCF
∴DE=BF
∴四边形DEBF是平行四边形
(四)小结归纳
通过这节课的学习,你有什么感悟?
分类梳理,优化结构
一题多解,选择应用
一题多变,反思归纳
(五)布置作业
必做题:教科书习题18.1 第4,6题
选做题:教科书习题18.1 第15题
目标检测设计
1..一个四边形的边长依次为a,b,c,d,且满足a2+b2+c2+d2=2ac+2bd,则这个四边形为 .?
解:∵a2+b2+c2+d2=2ac+2bd
∴(a-c)2+(b-d)2=0
∴ a-c=0,b-d=0,
则a=c,b=d,
因此四边形为平行四边形
平行四边形
2.在四边形ABCD中,AB∥CD,AD∥BC,AC与BC相交于点O,且AC=12,则AO=
6
解: ∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
∵AC与BC相交于点O,且AC=12,
∴AO=6
2. 已知:如图,E,F是平行四边形ABCD对角线BD上的两点,BE=DF,点G,H分别在BA和DC的延长线上,且AG=CH,连接GE,EH,HF,FG,求证:四边形GEFH是平行四边形。
G
A
B
D
C
H
E
F
证明:∵四边形ABCD是平行四边形
∴AB=CBD∠ABE=∠CDF
∵AG=CH
∴BG=DH
∵BE=DF
∴△BEG≌△DFH
∴GE=HF ∠BEG=∠DFH
∴∠GEF=∠HFE
∴GE∥HF
因此四边形DEBF是平行四边形
4.如图,分别以直角三角形ABC的三边长为边长,在BC的同侧作为等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF,求证:四边形ADEF是平行四边形。
A
D
B
C
F
E
证明:∵△ABD,△BCE,△ACE是等边三角形
∴BD=BA,BE=BC,AC=AF
∠ABD=∠BDA=∠BAD=∠CAF=∠CBE=60°
∴∠ABD-∠ABE=∠CBE-∠ABE
即∠DBE=∠ABC
∴△DBE≌△ABC
∴DE=AC=AF,∠BDE=∠BAC
∵∠BAC=90°,∠BDA=60°
∴∠ADE=∠BDE-∠BDA=30°
∵∠DAF=360°-∠BAD-∠BAC-∠CAF
=150°
∴∠ADE+∠DAF=180°
即DE∥AF
又∵DE=AF
∴四边形ADEF是平行四边形.
谢谢大家,再见!
18.1.3平行四边形判定定理的简单应用
Ⅰ教学目标:
1)进一步理解和掌握平行四边形的判定
2)灵活运用平行四边形判定解决实际问题
Ⅱ教学重难点:
重点是:平行四边形的运用
难点是:平行四边形的灵活运用
教学过程设计
(一)复习知识,形成简约的知识结构
问题 (1)平行四边形的判定定理分别是从哪些方面得到的?
研究顺序:定义-边-角-对角线
(2)请说说这些平行四边形的判定定理。
1.两组对边分别相等的四边形是平行四边形
2.两组对角分别相等的四边形是平行四边形
3.对角线互相平分的四边形是平行四边形
4.一组对边既平行又相等的四边形是平行四边形
5.两组对边分别平行的四边形是平行四边形?
边 角 对角线
平行四边形
(3)你能选择恰当的角度对平行四边形的判定定理进行分类吗?(请用表格呈现)
1)两组对边分别平行的四边形是平行四边形(定义)
?2)两组对边分别相等的四边形是平行四边形?
3)一组对边既平行又相等的四边形是平行四边形?
两组对角分别相等的四边形是平行四边形
对角线互相平分
的四边形是平行四边形
追问:1)判定平行四边形的条件有几个?
2)一组对边平行,另一组对边相等的四边形是平行四边形吗?
2个
等腰梯形
1.在四边形ABCD中,对角线AC、BD交于点O,在横线上添加什么条件能使四边形ABCD是平行四边形
1)若AB‖CD, ,则四边形ABCD是平行四边形;
若AB‖CD, ,则四边形ABCD是平行四边形;
2)若AB=CD, ,则四边形ABCD是平行四边形;
若AO=DO, ,则四边形ABCD是平行四边形;
O
A
B
C
D
AC‖ BD
AB=CD
AC=BD
BO=CO
(二)基础练习,强化应用
1.在下列给出的条件中,能判定四边形ABCD是平行四边形的是( )
A:∠A=∠B,∠C=∠D B:AB=CD,AD=BC
C:AB=AD,CB=CD, D:AB∥CD,AD=BC
2.四边形ABCD中,若∠A+∠B=180°,∠C+∠D=180°,则这个四边形
(填“是”“不是”或“不一定是”)平行四边形.?
3.已知,如图,ED∥AC,点B在AC上,且AB=CD=ED,找出图中的平行四边形,并说明理由。
E
A
B
C
D
B
解:四边形EABD和四边形EBCD是平行四边形
理由:∵ED∥AC,AB=CD=ED
∴四边形EABD和四边形
EBCD是平行四边形
不一定是
4.顺次连接四边形各边中点能得到 形.
D
A
B
E
C
F
G
H
证明:依题意,如图示,在四边形ABCD中,点E,F,G,H分别是边AB,BC,CD,DA上的中点,连接点E,F,G,H,试证明四边形EFGH为平行四边形
连接AC
∵点E,F,G,H分别是边AB,BC,CD,DA上的中点
∴EF∥AC,HG∥AC
EF= 1/2 AC ,HG= 1/2 AC
∴EF∥GH且EF=GH
∴四边形EFGH为平行四边形
平行四边
(三)典例引领,深化应用
例1 已知:如图,E,F是平行四边形ABCD对角线上的两点,AE=CF。求证:四边形DEBF是平行四边形。
D
A
B
C
E
F
证明:∵四边形ABCD是平行四边形
∴AD=CB,∠DAE=∠BCF
∵AE=CF
∴△ADE≌△CBF
∴DE=BF ∠AED=∠CFB
∴∠DEF=∠BFE
∴DE∥BF
因此四边形DEBF是平行四边形
追问1:还有其他方法吗?
A
D
C
B
E
F
O
证明:连接BD,交AC于点O
∵四边形ABCD是平行四边形
∴AO=CO,BO=DO
∵AE=CF
∴EO=FO
∴四边形DEBF是平行四边形
变式1:若将题目条件AE=CF改为DE⊥AC,BF⊥AC,其他条件不变,四边形DEBF还是平行四边形吗?并证明(是平行四边形)
C
D
A
B
E
F
∟
∟
证明:∵四边形ABCD是平行四边形
∴AD=CB ,∠DAE=∠BCF
∵DE⊥AC,BF⊥AC,
∴∠DEF=∠BFE,DE∥BF
∴△ADE≌△BCF
∴DE=BF
∴四边形DEBF是平行四边形
(四)小结归纳
通过这节课的学习,你有什么感悟?
分类梳理,优化结构
一题多解,选择应用
一题多变,反思归纳
(五)布置作业
必做题:教科书习题18.1 第4,6题
选做题:教科书习题18.1 第15题
目标检测设计
1..一个四边形的边长依次为a,b,c,d,且满足a2+b2+c2+d2=2ac+2bd,则这个四边形为 .?
解:∵a2+b2+c2+d2=2ac+2bd
∴(a-c)2+(b-d)2=0
∴ a-c=0,b-d=0,
则a=c,b=d,
因此四边形为平行四边形
平行四边形
2.在四边形ABCD中,AB∥CD,AD∥BC,AC与BC相交于点O,且AC=12,则AO=
6
解: ∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
∵AC与BC相交于点O,且AC=12,
∴AO=6
2. 已知:如图,E,F是平行四边形ABCD对角线BD上的两点,BE=DF,点G,H分别在BA和DC的延长线上,且AG=CH,连接GE,EH,HF,FG,求证:四边形GEFH是平行四边形。
G
A
B
D
C
H
E
F
证明:∵四边形ABCD是平行四边形
∴AB=CBD∠ABE=∠CDF
∵AG=CH
∴BG=DH
∵BE=DF
∴△BEG≌△DFH
∴GE=HF ∠BEG=∠DFH
∴∠GEF=∠HFE
∴GE∥HF
因此四边形DEBF是平行四边形
4.如图,分别以直角三角形ABC的三边长为边长,在BC的同侧作为等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF,求证:四边形ADEF是平行四边形。
A
D
B
C
F
E
证明:∵△ABD,△BCE,△ACE是等边三角形
∴BD=BA,BE=BC,AC=AF
∠ABD=∠BDA=∠BAD=∠CAF=∠CBE=60°
∴∠ABD-∠ABE=∠CBE-∠ABE
即∠DBE=∠ABC
∴△DBE≌△ABC
∴DE=AC=AF,∠BDE=∠BAC
∵∠BAC=90°,∠BDA=60°
∴∠ADE=∠BDE-∠BDA=30°
∵∠DAF=360°-∠BAD-∠BAC-∠CAF
=150°
∴∠ADE+∠DAF=180°
即DE∥AF
又∵DE=AF
∴四边形ADEF是平行四边形.
谢谢大家,再见!
