人教版六年级下册数学反比例的意义 课件(49张ppt)
文档属性
| 名称 | 人教版六年级下册数学反比例的意义 课件(49张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-24 21:26:53 | ||
图片预览








文档简介
(共49张PPT)
反比例的意义
六年级 数学
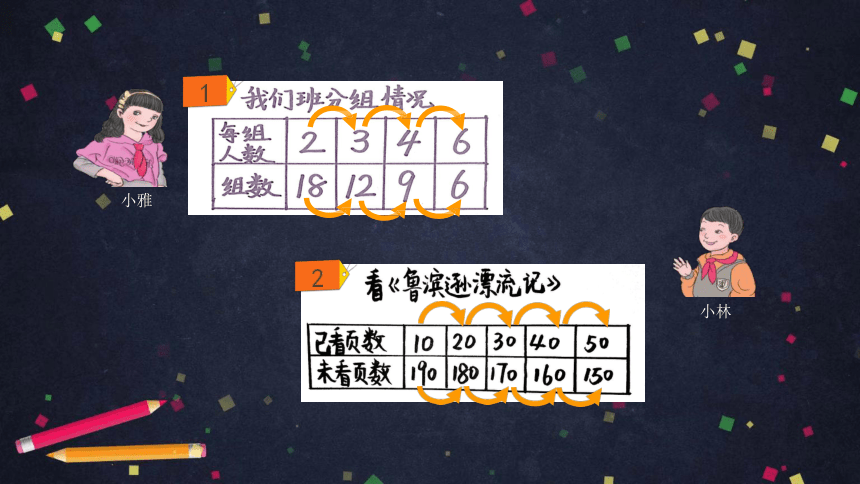
小雅
两种相关联的量,一种量变化, 另一种量也随着变化,如果这两种量 中相对应的两个数的比值一定,这两 种量就叫做成正比例的量,它们的关 系叫做正比例关系。
?
?=k
(一定)
正 比 例
1小时行驶80km,
2小时行驶160km,
3小时行驶240km。
……
汽车行驶的速度一定。
小雅
正 比 例
汽车行驶的路程与时间成正比例关系。
汽车行驶的路程和时间是两种相关联的量。
路程
时间
= 速度(一定)
1小时行驶80km,
2小时行驶160km,
3小时行驶240km。
……
汽车行驶的速度一定。
有正比例, 也应该 有反比例?
两种相关联的量有什 么变化规律?是不是 也有不变的量?
正 比 例
反 比 例
小西
可以从生活中找一些例子 来研究。
收集数据,列表观 察、列式计算……
小茹
正 比 例
反 比 例
猜想
小雅
小林
小菲
如果每段长10cm,这条彩带能剪60段。 如果每段长20cm,这条彩带能剪30段。
把一条彩带剪成若干段,每段长度相等。
把相同体积的水倒入 底面积不同的杯子。
如果把这些水倒入
①号杯子,水面最
高;如果倒入⑤号 杯子,水面最低。
小林
杯子的底面积和水 的高度是变化的量。
杯子的底面积越小, 水的高度就越大;
杯子的底面积越大, 水的高度就越小。
把相同体积的水倒入 底面积不同的杯子。
杯子的底面积/cm? 10 15 20 30 60 …
水的高度/cm 30 20 15 10 5 …
⑤
① ② ③ ④
杯子的底面积与水的高度的变化情况如下表。
把相同体积的水倒入 底面积不同的杯子。
增加
减少
小茹
2 × 18 = 36(人)
3 × 12 = 36(人)
4 × 9 = 36(人)
6 × 6 = 36(人)
小天
2 × 18 = 36(人)
3 × 12 = 36(人)
4 × 9 = 36(人)
6 × 6 = 36(人)
每组人数×组数=总人数
小茹
小天
2 × 18 = 36(人)
3 × 12 = 36(人)
4 × 9 = 36(人)
6 × 6 = 36(人)
小茹
每组人数×组数=总人数
×1.5
÷1.5
÷2
×2
组数和每组人数是相关联的量,组数是随着 每组人数的变化而变化的,而且每组人数和组数 的乘积是一定的。
小天
×1.5
÷1.5
÷2
×2
已看页数+未看页数=总页数
小明
一种量乘几,另一种量就相应的除 以几,两种量的乘积一定。
段数 = 彩带总长度
每段长度×
底面积×高度 = 体积
÷1.5
10 × 30 = 300(cm?)
15 × 20 = 300(cm?)
20 × 15 = 300(cm?)
×1.5
÷2
×2
……
×2
÷2
1、3、4号是一类,
2号是一类。
× +
+
+
+
+
+
×
×
×
×
× ×
× ×
× ×
× ×
× ×
× ×
反比例关系 应该是乘积 一定?
?=k(一定)
正比例关系:丽丽
?
× +
+
+
+
+
+
×
×
×
×
× ×
× ×
× ×
× ×
× ×
× ×
像这样,两种相关联的量,一种量变化,另一种量也随着变 化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫
做成反比例的量,它们的关系叫做反比例关系。
如果用字母x和y表示两种相关联的量,用k表示它们的积
(一定),反比例关系可以用下面的式子表示:
xy=k
变化,另一种量也随着变化。
变化,另一种量也随着变化。
正比例
两种相关联的量,一种量
反比例
两种相关联的量,一种量
?=k(一定)
xy=k(一定)
这两种量就叫做成成反反比比例例的的量量。。
?
这两种量就叫做成成正正比比例例的的量量。。
哪两种量成反比例关系?
组数与每组人数成反比例关系。
每组人数×组数 = 总人数 (一定)
亮亮
2 × 18 = 36(人)
3 × 12 = 36(人)
4 × 9 = 36(人)
6 × 6 = 36(人)
组数和每组人数是两种相关联的量。
每段长度×段数=彩带总长度(一定)
段数与每段长度成反比例关系。
底面积 × 高度 = 体积(一定)
段数和每段长度是两种相关联的量。 水的高度和杯子底面积是两种相关联的量。
水的高度与杯子底面积成反比例关系。
未看页数和已看页数是两种相关联的量。
已看页数+未看页数=总页数(一定) 未看页数与已看页数不成反比例关系。
表中有哪两种量?它们是不是相关联 的量?这两种量成反比例关系吗?
杯子的容量/mL 100 150 200 300 …
所需杯子数量/个 12 8 6 4 …
小明
把一桶果汁倒入容量不同的杯子,杯子的容量与所需杯子 数量如下表。
100 × 12 = 1200(mL)
150 × 8 = 1200(mL)
200 × 6 = 1200(mL)
300 × 4 = 1200(mL)
所需杯子数量和杯子的容量是两种相关联的量。
小明
把一桶果汁倒入容量不同的杯子,杯子的容量与所需杯子 数量如下表。
杯子的容量/mL 100 150 200 300 …
所需杯子数量/个 12 8 6 4 …
所需杯子数量和杯子的容量是两种相关联的量。 杯子的容量×所需杯子数量=果汁总体积(一定) 所需杯子数量与杯子的容量成反比例关系。
小明
把一桶果汁倒入容量不同的杯子,杯子的容量与所需杯子 数量如下表。
杯子的容量/mL 100 150 200 300 …
所需杯子数量/个 12 8 6 4 …
给教室铺地砖。如果用大瓷砖铺,用的瓷砖的 块数就少;如果用小瓷砖铺,用的瓷砖的块数 就多。
小军
每块地砖的面积/cm? 900 1800 3600
所需地砖数量/块 600 300 150
小菲
怎么判断是不是成反比例关系呢?
给一间长9m,宽6m的教室铺地砖,每块地砖的面积与 所需地砖数量如下表。
每块地砖的面积/cm? 900 1800 3600
所需地砖数量/块 600 300 150
这两种量与教室面积之间是什么关系?
小慧
给一间长9m,宽6m的教室铺地砖,每块地砖的面积与 所需地砖数量如下表。
给一间长9m,宽6m的教室铺地砖,每块地砖的面积与
所需地砖数量如下表。
每块地砖的面积/cm? 900 1800 3600
所需地砖数量/块 600 300 150
小菲
900 ×600 = 554400000000(cm?)
1800 ×300 = 540000(cm?)
3600 ×150 = 554400000000(cm?)
教室面积一定
9 × 6 = 54(m?)
给一间长9m,宽6m的教室铺地砖,每块地砖的面积与
所需地砖数量如下表。
每块地砖的面积/cm? 900 1800 3600
所需地砖数量/块 600 300 150
小菲
所需地砖数量和每块地砖的面积是两种相关联的量。
每块地砖的面积×所需地砖数量=教室面积(一定)
所需地砖数量与每块地砖的面积成反比例关系。
小慧
东东
怎么判断呢?
可以借助数据 分析。
谁和谁是相关联的量?相关联的两 种量与不变量又是什么关系呢?
判断下面各题中的两种量是否成反比例关系,并说明理由。
路程一定,汽车行驶的时间与速度。
一条路,未修的长度与已修的长度。
苹果的单价一定,购买苹果的总价与数量。
平行四边形面积一定,它的高与底。
练一练
小刚
小军
第1、3、4题中两种量成反比例关系。
第2题中两种量不成反比例关系。
第1、4题中两种量量成 成反反比比例例关关系系。。第第 22、、3题题中中两两种种
量不成反比例关系。
1.路程一定,汽车行驶的时间与速度。
汽车行驶的时间和速度是两种相关联的量。
汽车行驶的时间与速度成反比例关系。
速度 × 时间 =
路程(一定)
东东
小明
4.平行四边形面积一定,它的高与底。
小菲
2.一条路,未修的长度与已修的长度。
小林
3.苹果的单价一定,购买苹果的总价与数量。
小刚
购买苹果的总价与数 量不成反比例关系。
小军
单价×数量=总价
3.苹果的单价一定,购买苹果的总价与数量。
小刚
购买苹果的总价 与数量成反比例 关系。
购买苹果的总价与数 量不成反比例关系。
小军
3.苹果的单价一定,购买苹果的总价与数量。
购买苹果的总价和数量是两种相关联的量。
数量
购买苹果的总价与数量成正比例关系。
总价
= 单价(一定)
小刚
你有什么收获?
我们利用研究正比例意 义的方法来研究反比例 的意义。
学习了反比例的 意义,会判断两 种量是否成反比 例关系。
在判断反比例关系时,
可以举例帮助分析。
作业1:数学书第51页第11题
11.判断下面各题中的两种量是否成反比例关系,并说明理由。
煤的数量一定,使用天数与每天的平均用煤量。
全班的人数一定,按各组人数相等的要求分组,组数与每组的人数。
圆柱体积一定,圆柱的底面积与高。
在一块菜地上种的黄瓜与西红柿的面积。
书的总册数一定,按各包册数相等的规定包装书,包数与每包的册数。
作业2:找一找
发现生活中成反比例关系的量,并记录下来。
再 见
反比例的意义
六年级 数学
小雅
两种相关联的量,一种量变化, 另一种量也随着变化,如果这两种量 中相对应的两个数的比值一定,这两 种量就叫做成正比例的量,它们的关 系叫做正比例关系。
?
?=k
(一定)
正 比 例
1小时行驶80km,
2小时行驶160km,
3小时行驶240km。
……
汽车行驶的速度一定。
小雅
正 比 例
汽车行驶的路程与时间成正比例关系。
汽车行驶的路程和时间是两种相关联的量。
路程
时间
= 速度(一定)
1小时行驶80km,
2小时行驶160km,
3小时行驶240km。
……
汽车行驶的速度一定。
有正比例, 也应该 有反比例?
两种相关联的量有什 么变化规律?是不是 也有不变的量?
正 比 例
反 比 例
小西
可以从生活中找一些例子 来研究。
收集数据,列表观 察、列式计算……
小茹
正 比 例
反 比 例
猜想
小雅
小林
小菲
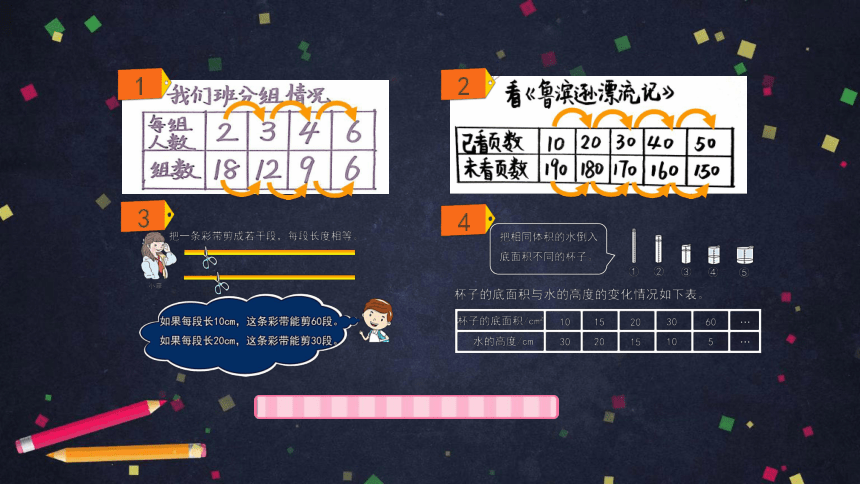
如果每段长10cm,这条彩带能剪60段。 如果每段长20cm,这条彩带能剪30段。
把一条彩带剪成若干段,每段长度相等。
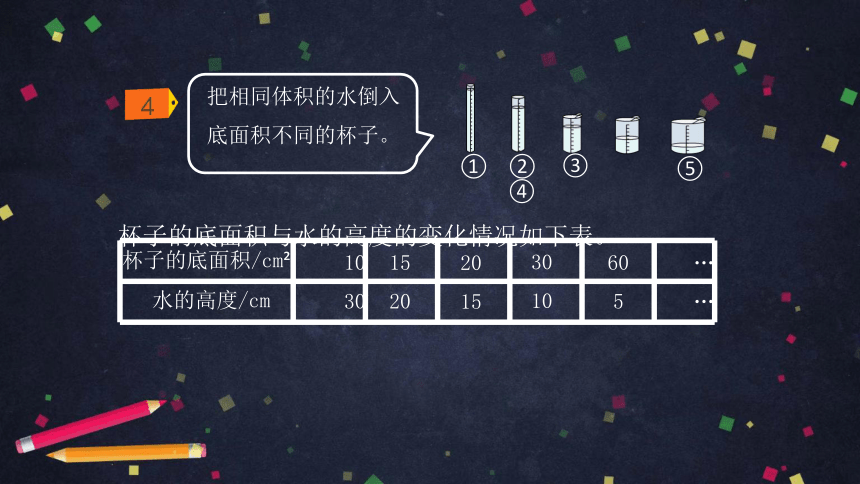
把相同体积的水倒入 底面积不同的杯子。
如果把这些水倒入
①号杯子,水面最
高;如果倒入⑤号 杯子,水面最低。
小林
杯子的底面积和水 的高度是变化的量。
杯子的底面积越小, 水的高度就越大;
杯子的底面积越大, 水的高度就越小。
把相同体积的水倒入 底面积不同的杯子。
杯子的底面积/cm? 10 15 20 30 60 …
水的高度/cm 30 20 15 10 5 …
⑤
① ② ③ ④
杯子的底面积与水的高度的变化情况如下表。
把相同体积的水倒入 底面积不同的杯子。
增加
减少
小茹
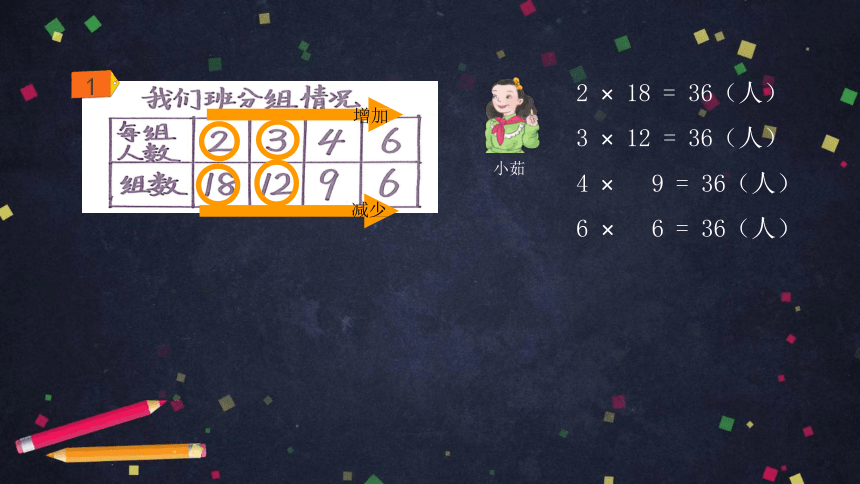
2 × 18 = 36(人)
3 × 12 = 36(人)
4 × 9 = 36(人)
6 × 6 = 36(人)
小天
2 × 18 = 36(人)
3 × 12 = 36(人)
4 × 9 = 36(人)
6 × 6 = 36(人)
每组人数×组数=总人数
小茹
小天
2 × 18 = 36(人)
3 × 12 = 36(人)
4 × 9 = 36(人)
6 × 6 = 36(人)
小茹
每组人数×组数=总人数
×1.5
÷1.5
÷2
×2
组数和每组人数是相关联的量,组数是随着 每组人数的变化而变化的,而且每组人数和组数 的乘积是一定的。
小天
×1.5
÷1.5
÷2
×2
已看页数+未看页数=总页数
小明
一种量乘几,另一种量就相应的除 以几,两种量的乘积一定。
段数 = 彩带总长度
每段长度×
底面积×高度 = 体积
÷1.5
10 × 30 = 300(cm?)
15 × 20 = 300(cm?)
20 × 15 = 300(cm?)
×1.5
÷2
×2
……
×2
÷2
1、3、4号是一类,
2号是一类。
× +
+
+
+
+
+
×
×
×
×
× ×
× ×
× ×
× ×
× ×
× ×
反比例关系 应该是乘积 一定?
?=k(一定)
正比例关系:丽丽
?
× +
+
+
+
+
+
×
×
×
×
× ×
× ×
× ×
× ×
× ×
× ×
像这样,两种相关联的量,一种量变化,另一种量也随着变 化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫
做成反比例的量,它们的关系叫做反比例关系。
如果用字母x和y表示两种相关联的量,用k表示它们的积
(一定),反比例关系可以用下面的式子表示:
xy=k
变化,另一种量也随着变化。
变化,另一种量也随着变化。
正比例
两种相关联的量,一种量
反比例
两种相关联的量,一种量
?=k(一定)
xy=k(一定)
这两种量就叫做成成反反比比例例的的量量。。
?
这两种量就叫做成成正正比比例例的的量量。。
哪两种量成反比例关系?
组数与每组人数成反比例关系。
每组人数×组数 = 总人数 (一定)
亮亮
2 × 18 = 36(人)
3 × 12 = 36(人)
4 × 9 = 36(人)
6 × 6 = 36(人)
组数和每组人数是两种相关联的量。
每段长度×段数=彩带总长度(一定)
段数与每段长度成反比例关系。
底面积 × 高度 = 体积(一定)
段数和每段长度是两种相关联的量。 水的高度和杯子底面积是两种相关联的量。
水的高度与杯子底面积成反比例关系。
未看页数和已看页数是两种相关联的量。
已看页数+未看页数=总页数(一定) 未看页数与已看页数不成反比例关系。
表中有哪两种量?它们是不是相关联 的量?这两种量成反比例关系吗?
杯子的容量/mL 100 150 200 300 …
所需杯子数量/个 12 8 6 4 …
小明
把一桶果汁倒入容量不同的杯子,杯子的容量与所需杯子 数量如下表。
100 × 12 = 1200(mL)
150 × 8 = 1200(mL)
200 × 6 = 1200(mL)
300 × 4 = 1200(mL)
所需杯子数量和杯子的容量是两种相关联的量。
小明
把一桶果汁倒入容量不同的杯子,杯子的容量与所需杯子 数量如下表。
杯子的容量/mL 100 150 200 300 …
所需杯子数量/个 12 8 6 4 …
所需杯子数量和杯子的容量是两种相关联的量。 杯子的容量×所需杯子数量=果汁总体积(一定) 所需杯子数量与杯子的容量成反比例关系。
小明
把一桶果汁倒入容量不同的杯子,杯子的容量与所需杯子 数量如下表。
杯子的容量/mL 100 150 200 300 …
所需杯子数量/个 12 8 6 4 …
给教室铺地砖。如果用大瓷砖铺,用的瓷砖的 块数就少;如果用小瓷砖铺,用的瓷砖的块数 就多。
小军
每块地砖的面积/cm? 900 1800 3600
所需地砖数量/块 600 300 150
小菲
怎么判断是不是成反比例关系呢?
给一间长9m,宽6m的教室铺地砖,每块地砖的面积与 所需地砖数量如下表。
每块地砖的面积/cm? 900 1800 3600
所需地砖数量/块 600 300 150
这两种量与教室面积之间是什么关系?
小慧
给一间长9m,宽6m的教室铺地砖,每块地砖的面积与 所需地砖数量如下表。
给一间长9m,宽6m的教室铺地砖,每块地砖的面积与
所需地砖数量如下表。
每块地砖的面积/cm? 900 1800 3600
所需地砖数量/块 600 300 150
小菲
900 ×600 = 554400000000(cm?)
1800 ×300 = 540000(cm?)
3600 ×150 = 554400000000(cm?)
教室面积一定
9 × 6 = 54(m?)
给一间长9m,宽6m的教室铺地砖,每块地砖的面积与
所需地砖数量如下表。
每块地砖的面积/cm? 900 1800 3600
所需地砖数量/块 600 300 150
小菲
所需地砖数量和每块地砖的面积是两种相关联的量。
每块地砖的面积×所需地砖数量=教室面积(一定)
所需地砖数量与每块地砖的面积成反比例关系。
小慧
东东
怎么判断呢?
可以借助数据 分析。
谁和谁是相关联的量?相关联的两 种量与不变量又是什么关系呢?
判断下面各题中的两种量是否成反比例关系,并说明理由。
路程一定,汽车行驶的时间与速度。
一条路,未修的长度与已修的长度。
苹果的单价一定,购买苹果的总价与数量。
平行四边形面积一定,它的高与底。
练一练
小刚
小军
第1、3、4题中两种量成反比例关系。
第2题中两种量不成反比例关系。
第1、4题中两种量量成 成反反比比例例关关系系。。第第 22、、3题题中中两两种种
量不成反比例关系。
1.路程一定,汽车行驶的时间与速度。
汽车行驶的时间和速度是两种相关联的量。
汽车行驶的时间与速度成反比例关系。
速度 × 时间 =
路程(一定)
东东
小明
4.平行四边形面积一定,它的高与底。
小菲
2.一条路,未修的长度与已修的长度。
小林
3.苹果的单价一定,购买苹果的总价与数量。
小刚
购买苹果的总价与数 量不成反比例关系。
小军
单价×数量=总价
3.苹果的单价一定,购买苹果的总价与数量。
小刚
购买苹果的总价 与数量成反比例 关系。
购买苹果的总价与数 量不成反比例关系。
小军
3.苹果的单价一定,购买苹果的总价与数量。
购买苹果的总价和数量是两种相关联的量。
数量
购买苹果的总价与数量成正比例关系。
总价
= 单价(一定)
小刚
你有什么收获?
我们利用研究正比例意 义的方法来研究反比例 的意义。
学习了反比例的 意义,会判断两 种量是否成反比 例关系。
在判断反比例关系时,
可以举例帮助分析。
作业1:数学书第51页第11题
11.判断下面各题中的两种量是否成反比例关系,并说明理由。
煤的数量一定,使用天数与每天的平均用煤量。
全班的人数一定,按各组人数相等的要求分组,组数与每组的人数。
圆柱体积一定,圆柱的底面积与高。
在一块菜地上种的黄瓜与西红柿的面积。
书的总册数一定,按各包册数相等的规定包装书,包数与每包的册数。
作业2:找一找
发现生活中成反比例关系的量,并记录下来。
再 见
