人教版B版(2019)高中数学必修第二册:第四章 指数函数、对数函数与幂函数 综合测试(word附答案与解析)
文档属性
| 名称 | 人教版B版(2019)高中数学必修第二册:第四章 指数函数、对数函数与幂函数 综合测试(word附答案与解析) |  | |
| 格式 | zip | ||
| 文件大小 | 894.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-26 10:02:48 | ||
图片预览




文档简介
第四章综合测试
一、单项选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知函数的定义域为,则函数的定义域为( )
A. B. C. D.
2.已知函数,则( )
A. B.0 C.1 D.2
3.设函数,若,则实数的取值范围为( )
A. B. C. D.
4.已知函数,若,,,则的大小关系为( )
A. B. C. D.
5.已知,是上的减函数,那么实数的取值范围是( )
A. B. C. D.
6.已知,且,若,则函数的图像为( )
A B C D
7.给出下列命题:
①函数为偶函数;
②函数在上单调递增;
③函数在区间上单调递减;
④函数与的图像关于直线对称。
其中正确命题的个数是( )
A.1 B.2 C.3 D.4
8.设函数,则下列命题中不正确的是( )
A.函数的定义域为 B.函数是增函数
C.函数的图像关于直线对称 D.函数的值域是
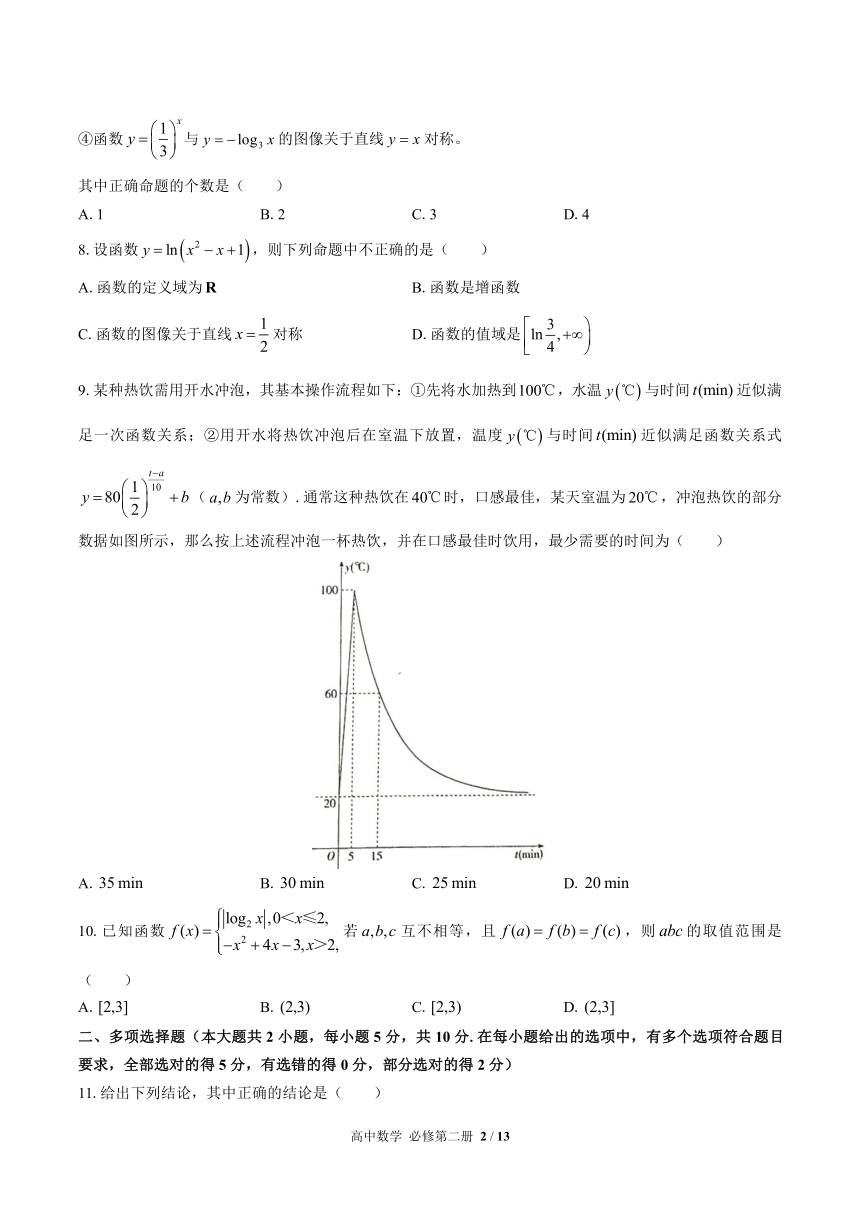
9.某种热饮需用开水冲泡,其基本操作流程如下:①先将水加热到,水温与时间近似满足一次函数关系;②用开水将热饮冲泡后在室温下放置,温度与时间近似满足函数关系式(为常数).通常这种热饮在时,口感最佳,某天室温为,冲泡热饮的部分数据如图所示,那么按上述流程冲泡一杯热饮,并在口感最佳时饮用,最少需要的时间为( )
A. B. C. D.
10.已知函数若互不相等,且,则的取值范围是( )
A. B. C. D.
二、多项选择题(本大题共2小题,每小题5分,共10分.在每小题给出的选项中,有多个选项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分)
11.给出下列结论,其中正确的结论是( )
A.函数的最大值为
B.已知函数(且)在上是减函数,则实数的取值范围是
C.在同一平面直角坐标系中,函数与的图像关于直线对称
D.已知定义在上的奇函数在内有1 010个零点,则函数的零点个数为2 021
12.定义“正对数”:若,,则下列结论中正确的是( )
A. B.
C. D.
三、填空题(本大题共4小题,每小题5分,共20分.将答案填在题中横线上)
13.已知为定义在上的奇函数,且当时,,则的值为________.
14.某新能源汽车公司为激励创新,计划逐年加大研发资金投入,若该公司2018年(记为第1年)全年投入研发资金5 300万元,在此基础上,以后每年投入的研发资金比上一年增长8%,则该公司全年投入的研发资金开始超过7 000万元的年份是________年.(参考数据:,,)
15.已知函数(且)在上的值域是.若函数的图像不经过第一象限,则的取值范围为________.
16.若不等式对一切恒成立,则实数的取值范围是________.
四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(10分)(1)计算的值;
(2)计算:.
18.(12分)已知幂函数在上单调递增,函数.
(1)求实数的值,并简要说明函数的单调性;
(2)若不等式恒成立,求实数的取值范围.
19.(12分)目前,我国一些高耗能低效产业(煤炭、钢铁、有色金属、炼化等)的产能过剩将严重影响生态文明建设,“去产能”将是一项重大任务.某企业从2018年开始,每年的产能比上一年减少的百分比为.
(1)设年后(2018年记为第1年)年产能为2017年的倍,请用,表示;
(2)若,则至少要到哪一年才能使年产能不超过2017年的?(参考数据:,)
20.(12分)已知函数,.
(1)当时,求函数的值域;
(2)若函数的最小值记为,求的最大值.
21.(12分)已知函数(其中均为常数,且)的图像经过点与点.
(1)求的值;
(2)设函数,若对任意的,存在,使得成立,求实数的取值范围.
22.(12分)已知函数是偶函数.
(1)求的值;
(2)设,若函数与的图像有且只有一个公共点,求实数的取值范围;
(3)若函数,是否存在实数使得最小值为0,若存在,求出的值;若不存在,请说明理由.
第四章综合测试
答案解析
一、
1.【答案】D
【解析】由,得,所以,所以.
2.【答案】C
,
,
.
3.【答案】A
【解析】函数在定义域内单调递增,,
不等式等价于,解得,故选A.
4.【答案】C
【解析】知函数为偶函数,且在为增函数,,,,所以,即.
5.【答案】B
【解析】由题意得
解得,故选B.
6.【答案】A
【解析】由题意,得,令,则,解得或(舍去),
所以,即,所以的图像即为的图像,故选A.
7.【答案】C
【解析】由,知为偶函数,因此①正确;由知在上单调递增,因此②正确;当时,,它在上是增函数,因此③错误;由知与的图像关于直线对称,因此④正确,故选C.
8.【答案】B
【解析】A中命题正确,恒成立,函数的定义域为;B中命题错误,函数在时是增函数,在时是减函数;C中命题正确,函数的图像关于直线对称:D中命题正确,由可得,函数的值域为.故选B.
9.【答案】C
【解析】由题图知,当时,函数图像是一条线段,当时,因为函数的解析式为,所以将和代入解析式,
得解得故函数的解析式为.令,解得,所以最少需要的时间为.
10.B根据已知画出函数的草图如下。
不妨设,,
,,
解得,由图可知,.
二、
1l.【答案】CD
【解析】A错,令,则的最大值为1,的最小值为;B错,函数(且)在上是减函数,解得;C正确,在同一平面直角坐标系中,函数与的图像关于直线对称;D正确,定义在上的奇函数在内有1 010个零点,在内有1 010个零点,且.函数的零点个数为.
故选CD.
12.【答案】AD
【解析】对于A,当,时,有,从而,,所以;当,时,有,从而,,所以.
所以当,时,,所以A正确。
对于B,当,时满足,,而,,
所以,所以B错误。
对于C,令,,则,,显然,所以C错误.
对于D,由“正对数”的定义知,当时,有,当,时,有,从而,,所以;当,时,有,
从而,,所以;当,时,有,从而,,所以;
当时,,,因为,所以,所以.
综上所述,当时,,所以D正确,故选AD.
三、
13.【答案】
【解析】因为为奇函数,所以.
14.【答案】2023
【解析】设从第年开始超过7 000万元,则,即,
,取,又,所以开始超过7 000万元的年份是2023年.
15.【答案】
【解析】由题意得,
当时,在上单调递减,无解;
当时,在上单调递增,解得.
,又的图像不经过第一象限,,解得,即的取值范围是.
16.【答案】
【解析】对一切恒成立等价于在上恒成立,即对一切恒成立.
,,
即,
,即,解得.
四、
17.【答案】(1)解:原式.
(2)解:原式
.
18.【答案】(1)解:因为是幂函数,所以,解得或.
又因为在上单调递增,
所以,即,
所以,则
因为与均在上单调递增,
所以函数在上单调递增.
(2)易知的定义域为.因为,所以是奇函数,所以不等式可变为.
由(1)知在上单调递增,所以,解得.
19.【答案】(1)解:设2017年的产能为1.依题意得,
,.
(2)设年后年产能不超过2017年的,则,即,
解得,即,
,且,
的最小值为14,
.
至少要到2031年才能使年产能不超过2017年的.
20.【答案】(1)解:当时,,
由得.
因此,当时,;
当时,.
故的值域为.
(2)解:,.
令,,则,易知为二次函数,其图像的对称轴为直线.
①当时,;
②当是,;
③当时,.
所以
所以.
21.【答案】(1)解:由已知得消去得,即,又且,
所以,.
(2)由(1)知函数的解析式为,的解析式为.
当时,函数单调递增,其值域为.
令,当时,,于是,易得.
设函数,则函数的值域为,根据条件知,于是
解得.
所以实数的取值范围为.
22.【答案】(1)由函数是偶函数可知,
,
,即对一切恒成立,.
(2)函数与的图像有且只有一个公共点,
方程有且只有一个实根,
方程有且只有一个实根.
令,则方程有且只有一个正根.
①当时。方程即为,解得,不符合题意;
②当时,若方程有两个相等的正根,则,即,解得或,
当时,解得,不符合题意;
当时,解得;若方程有一个正根与一个负根,则解得.
以上结果经过验证均满足.
综上,实数的取值范围是.
(3)解:存在。理由:由题意得,.
令,则,则,,
易知的图像开口向上,对称轴为,
当,即时,,;
当,即时,,(含去):
当,即时,,(舍去).
综上,存在使得的最小值为0.
高中数学 必修第二册 4 / 5
一、单项选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知函数的定义域为,则函数的定义域为( )
A. B. C. D.
2.已知函数,则( )
A. B.0 C.1 D.2
3.设函数,若,则实数的取值范围为( )
A. B. C. D.
4.已知函数,若,,,则的大小关系为( )
A. B. C. D.
5.已知,是上的减函数,那么实数的取值范围是( )
A. B. C. D.
6.已知,且,若,则函数的图像为( )
A B C D
7.给出下列命题:
①函数为偶函数;
②函数在上单调递增;
③函数在区间上单调递减;
④函数与的图像关于直线对称。
其中正确命题的个数是( )
A.1 B.2 C.3 D.4
8.设函数,则下列命题中不正确的是( )
A.函数的定义域为 B.函数是增函数
C.函数的图像关于直线对称 D.函数的值域是
9.某种热饮需用开水冲泡,其基本操作流程如下:①先将水加热到,水温与时间近似满足一次函数关系;②用开水将热饮冲泡后在室温下放置,温度与时间近似满足函数关系式(为常数).通常这种热饮在时,口感最佳,某天室温为,冲泡热饮的部分数据如图所示,那么按上述流程冲泡一杯热饮,并在口感最佳时饮用,最少需要的时间为( )
A. B. C. D.
10.已知函数若互不相等,且,则的取值范围是( )
A. B. C. D.
二、多项选择题(本大题共2小题,每小题5分,共10分.在每小题给出的选项中,有多个选项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分)
11.给出下列结论,其中正确的结论是( )
A.函数的最大值为
B.已知函数(且)在上是减函数,则实数的取值范围是
C.在同一平面直角坐标系中,函数与的图像关于直线对称
D.已知定义在上的奇函数在内有1 010个零点,则函数的零点个数为2 021
12.定义“正对数”:若,,则下列结论中正确的是( )
A. B.
C. D.
三、填空题(本大题共4小题,每小题5分,共20分.将答案填在题中横线上)
13.已知为定义在上的奇函数,且当时,,则的值为________.
14.某新能源汽车公司为激励创新,计划逐年加大研发资金投入,若该公司2018年(记为第1年)全年投入研发资金5 300万元,在此基础上,以后每年投入的研发资金比上一年增长8%,则该公司全年投入的研发资金开始超过7 000万元的年份是________年.(参考数据:,,)
15.已知函数(且)在上的值域是.若函数的图像不经过第一象限,则的取值范围为________.
16.若不等式对一切恒成立,则实数的取值范围是________.
四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(10分)(1)计算的值;
(2)计算:.
18.(12分)已知幂函数在上单调递增,函数.
(1)求实数的值,并简要说明函数的单调性;
(2)若不等式恒成立,求实数的取值范围.
19.(12分)目前,我国一些高耗能低效产业(煤炭、钢铁、有色金属、炼化等)的产能过剩将严重影响生态文明建设,“去产能”将是一项重大任务.某企业从2018年开始,每年的产能比上一年减少的百分比为.
(1)设年后(2018年记为第1年)年产能为2017年的倍,请用,表示;
(2)若,则至少要到哪一年才能使年产能不超过2017年的?(参考数据:,)
20.(12分)已知函数,.
(1)当时,求函数的值域;
(2)若函数的最小值记为,求的最大值.
21.(12分)已知函数(其中均为常数,且)的图像经过点与点.
(1)求的值;
(2)设函数,若对任意的,存在,使得成立,求实数的取值范围.
22.(12分)已知函数是偶函数.
(1)求的值;
(2)设,若函数与的图像有且只有一个公共点,求实数的取值范围;
(3)若函数,是否存在实数使得最小值为0,若存在,求出的值;若不存在,请说明理由.
第四章综合测试
答案解析
一、
1.【答案】D
【解析】由,得,所以,所以.
2.【答案】C
,
,
.
3.【答案】A
【解析】函数在定义域内单调递增,,
不等式等价于,解得,故选A.
4.【答案】C
【解析】知函数为偶函数,且在为增函数,,,,所以,即.
5.【答案】B
【解析】由题意得
解得,故选B.
6.【答案】A
【解析】由题意,得,令,则,解得或(舍去),
所以,即,所以的图像即为的图像,故选A.
7.【答案】C
【解析】由,知为偶函数,因此①正确;由知在上单调递增,因此②正确;当时,,它在上是增函数,因此③错误;由知与的图像关于直线对称,因此④正确,故选C.
8.【答案】B
【解析】A中命题正确,恒成立,函数的定义域为;B中命题错误,函数在时是增函数,在时是减函数;C中命题正确,函数的图像关于直线对称:D中命题正确,由可得,函数的值域为.故选B.
9.【答案】C
【解析】由题图知,当时,函数图像是一条线段,当时,因为函数的解析式为,所以将和代入解析式,
得解得故函数的解析式为.令,解得,所以最少需要的时间为.
10.B根据已知画出函数的草图如下。
不妨设,,
,,
解得,由图可知,.
二、
1l.【答案】CD
【解析】A错,令,则的最大值为1,的最小值为;B错,函数(且)在上是减函数,解得;C正确,在同一平面直角坐标系中,函数与的图像关于直线对称;D正确,定义在上的奇函数在内有1 010个零点,在内有1 010个零点,且.函数的零点个数为.
故选CD.
12.【答案】AD
【解析】对于A,当,时,有,从而,,所以;当,时,有,从而,,所以.
所以当,时,,所以A正确。
对于B,当,时满足,,而,,
所以,所以B错误。
对于C,令,,则,,显然,所以C错误.
对于D,由“正对数”的定义知,当时,有,当,时,有,从而,,所以;当,时,有,
从而,,所以;当,时,有,从而,,所以;
当时,,,因为,所以,所以.
综上所述,当时,,所以D正确,故选AD.
三、
13.【答案】
【解析】因为为奇函数,所以.
14.【答案】2023
【解析】设从第年开始超过7 000万元,则,即,
,取,又,所以开始超过7 000万元的年份是2023年.
15.【答案】
【解析】由题意得,
当时,在上单调递减,无解;
当时,在上单调递增,解得.
,又的图像不经过第一象限,,解得,即的取值范围是.
16.【答案】
【解析】对一切恒成立等价于在上恒成立,即对一切恒成立.
,,
即,
,即,解得.
四、
17.【答案】(1)解:原式.
(2)解:原式
.
18.【答案】(1)解:因为是幂函数,所以,解得或.
又因为在上单调递增,
所以,即,
所以,则
因为与均在上单调递增,
所以函数在上单调递增.
(2)易知的定义域为.因为,所以是奇函数,所以不等式可变为.
由(1)知在上单调递增,所以,解得.
19.【答案】(1)解:设2017年的产能为1.依题意得,
,.
(2)设年后年产能不超过2017年的,则,即,
解得,即,
,且,
的最小值为14,
.
至少要到2031年才能使年产能不超过2017年的.
20.【答案】(1)解:当时,,
由得.
因此,当时,;
当时,.
故的值域为.
(2)解:,.
令,,则,易知为二次函数,其图像的对称轴为直线.
①当时,;
②当是,;
③当时,.
所以
所以.
21.【答案】(1)解:由已知得消去得,即,又且,
所以,.
(2)由(1)知函数的解析式为,的解析式为.
当时,函数单调递增,其值域为.
令,当时,,于是,易得.
设函数,则函数的值域为,根据条件知,于是
解得.
所以实数的取值范围为.
22.【答案】(1)由函数是偶函数可知,
,
,即对一切恒成立,.
(2)函数与的图像有且只有一个公共点,
方程有且只有一个实根,
方程有且只有一个实根.
令,则方程有且只有一个正根.
①当时。方程即为,解得,不符合题意;
②当时,若方程有两个相等的正根,则,即,解得或,
当时,解得,不符合题意;
当时,解得;若方程有一个正根与一个负根,则解得.
以上结果经过验证均满足.
综上,实数的取值范围是.
(3)解:存在。理由:由题意得,.
令,则,则,,
易知的图像开口向上,对称轴为,
当,即时,,;
当,即时,,(含去):
当,即时,,(舍去).
综上,存在使得的最小值为0.
高中数学 必修第二册 4 / 5
