人教版B版(2019)高中数学必修第二册:第五章 统计与概率 综合测试试卷(word版含答案解析)
文档属性
| 名称 | 人教版B版(2019)高中数学必修第二册:第五章 统计与概率 综合测试试卷(word版含答案解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-26 00:00:00 | ||
图片预览



文档简介
第五章综合测试
一、单项选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列说法正确的是( )
A.甲、乙二人比赛,甲胜的概率为,则比赛5场,甲一定会胜3场
B.某医院治疗一种疾病的治愈率为10%,前9个病人没有治愈,则第10个病人一定治愈
C.随机试验的频率与概率相等
D.天气预报中,预报明天降水概率为90%,是指明天降水的可能性是90%
2.小波一星期的总开支分布如图1所示,一星期的食品开支如图2所示,则小波一星期的鸡蛋开支占总开支的百分比为( )
图1 图2
A.1% B.2% C.3% D.5%
3.如图是容量为100的某样本的质量的频率分布直方图,则由图可估计样本质量的中位数为( )
A.11 B.11.5 C.12 D.12.5
4.从一批羽毛球中任取一个,如果取到质量小于的概率是0.3,质量不小于的概率是0.32,那么质量在范围内的概率是( )
A.0.62 B.0.38 C.0.70 D.0.68
5.空气质量指数AQI是一种反映和评价空气质量的标准,AQI指数与空气质量对应如表所示:
AQI 0~50 51~100 101~150 151~200 201~300 300以上
空气质量 优 良 轻度污染 中度污染 重度污染 严重污染
下图是某城市2018年11月全月的AQI变化统计图.
根据统计图判断,下列结论正确的是( )
A.从整体上看,这个月的空气质量越来越差
B.从整体上看,前半月的空气质量好于后半月的空气质量
C.从AQI数据看,前半月的方差大于后半月的方差
D.从AQI数据看,前半月的平均值小于后半月的平均值
6.AQI(Air Quality Index,空气质量指数)是报告每日空气质量的参数,描述了空气清洁或污染的程度.AQI共分六级:一级优(0~50);二级良(51~100);三级轻度污染(101~150);四级中度污染(151~200);五级重度污染(201~300);六级严重污染(大于300).如图是某市2019年4月份随机抽取10天的AQI指数的茎叶图,利用该样本估计该市2020年4月份空气质量为优的天数为( )
A.3 B.4 C.12 D.21
7.黄冈市的天气预报显示,大别山区在今后的三天中,一天有强浓雾的概率为40%,现用随机模拟的方法计这三天中至少有两天有强浓雾的概率:先利用计算器产生0~9之间整数值的随机数,并用0,1,2,3,4,表示没有强浓雾,用6,7,8,9表示有强浓雾,再以每个随机数作为一组,代表三天的天气情况,产生了如20组随机数:
779 537 113 730 588 506 027 394 357 231
683 569 479 812 842 273 925 191 978 520
则这三天中至少有两天有强浓雾的概率近似为( )
A. B. C. D.
8.如果3个正整数可作为一个直角三角形三条边的长,则称这3个数为一组勾股数,从1,2,3,4,5中任取3个不同的数,则这3个数构成一组勾股数的概率为( )
A. B. C. D.
9.洛书古称龟书,是阴阳五行术数之源.在古代传说中有神龟出于洛水,其甲壳上有此图像,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,五方白圈皆阳数,四隅黑点为阴数,其各行各列及对角线点数之和皆为15.如图,若从4个阴数中随机抽取2个数,则能使这2个数与居中阳数之和等于15的概率是( )
A. B. C. D.
10.某公司10位员工的月工资(单位:元)为,其均值和方差分别为和,若从下月起每位员工的月工资增加100元,则这10位员工下月工资的均值和方差分别为( )
A. B.
C. D.
二、多项选择题(本大题共2小题,每小题5分,共10分.在每小题给出的选项中,有多个选项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分)
11.如图是某电视台主办的歌手大奖赛上七位评委为甲、乙两名选手打出的分数的茎叶图(其中为数字0~9中的一个),则下列结论中不正确的是( )
A.甲选手的平均分有可能和乙选手的平均分相等
B.甲选手的平均分有可能比乙选手的平均分高
C.甲选手得分的中位数比乙选手得分的中位数低
D.甲选手得分的众数比乙选手得分的众数高
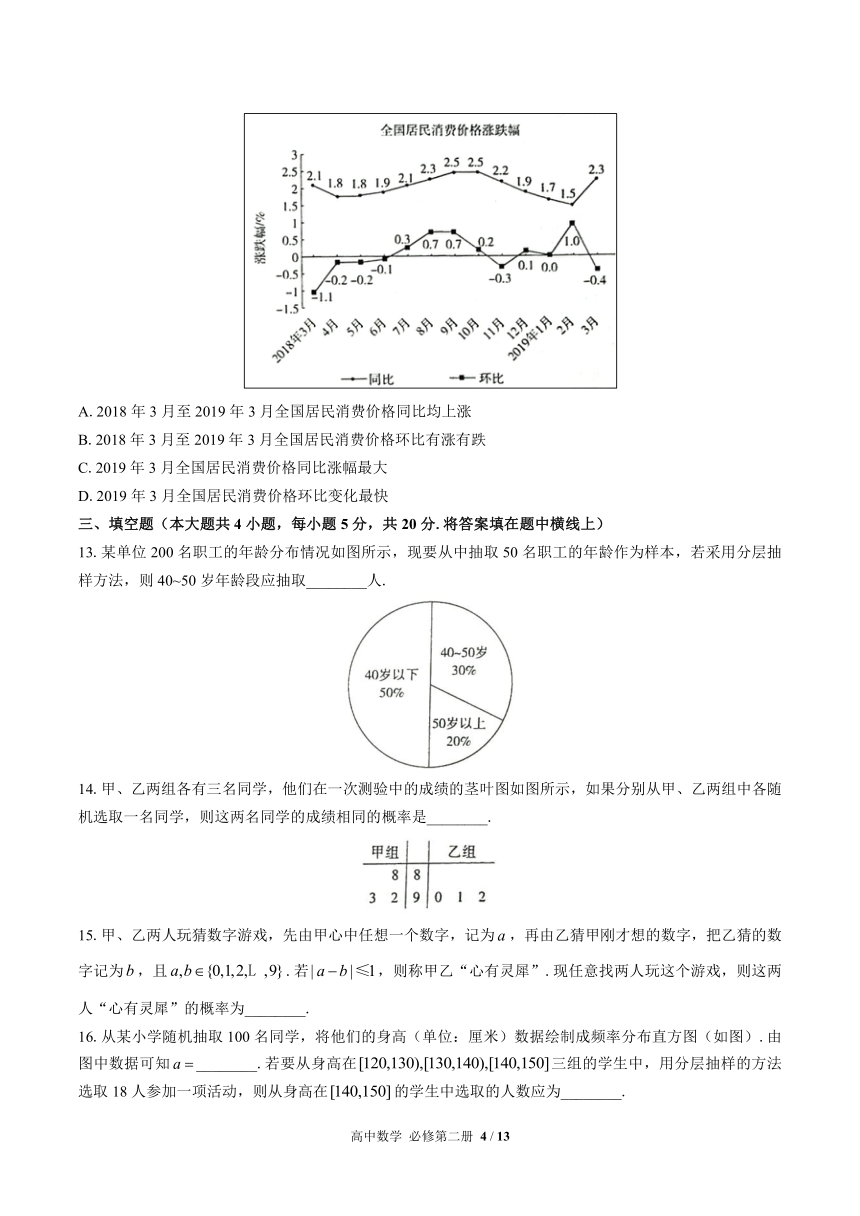
12.如图是国家统计局发布的2018年3月到2019年3月全国居民消费价格的涨跌幅情况折线图(注:2019年2月与2018年2月相比较称同比,2019年2月与2019年1月相比较称环比),根据该折线图,下列结论正确的是( )
A.2018年3月至2019年3月全国居民消费价格同比均上涨
B.2018年3月至2019年3月全国居民消费价格环比有涨有跌
C.2019年3月全国居民消费价格同比涨幅最大
D.2019年3月全国居民消费价格环比变化最快
三、填空题(本大题共4小题,每小题5分,共20分.将答案填在题中横线上)
13.某单位200名职工的年龄分布情况如图所示,现要从中抽取50名职工的年龄作为样本,若采用分层抽样方法,则40~50岁年龄段应抽取________人.
14.甲、乙两组各有三名同学,他们在一次测验中的成绩的茎叶图如图所示,如果分别从甲、乙两组中各随机选取一名同学,则这两名同学的成绩相同的概率是________.
15.甲、乙两人玩猜数字游戏,先由甲心中任想一个数字,记为,再由乙猜甲刚才想的数字,把乙猜的数字记为,且.若,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则这两人“心有灵犀”的概率为________.
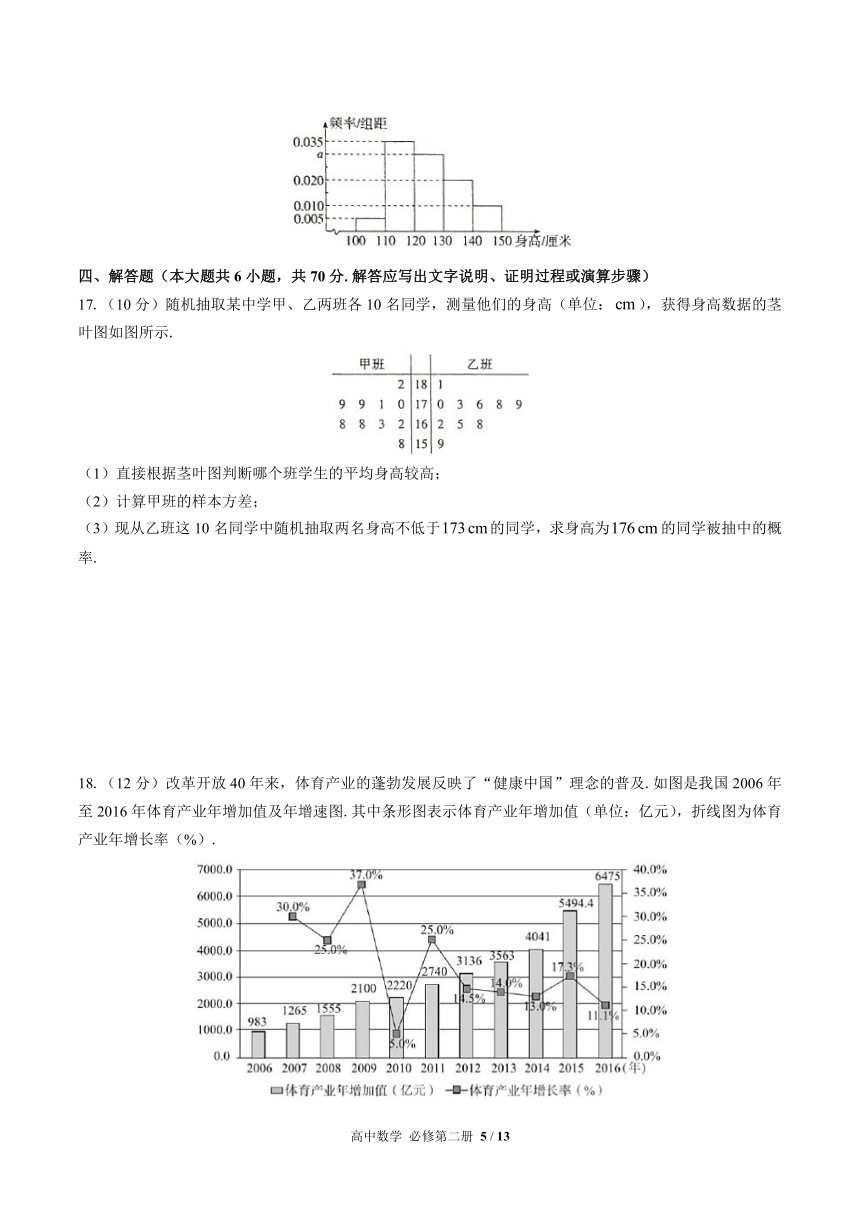
16.从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).由图中数据可知________.若要从身高在三组的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在的学生中选取的人数应为________.
四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(10分)随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:),获得身高数据的茎叶图如图所示.
(1)直接根据茎叶图判断哪个班学生的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于的同学,求身高为的同学被抽中的概率.
18.(12分)改革开放40年来,体育产业的蓬勃发展反映了“健康中国”理念的普及.如图是我国2006年至2016年体育产业年增加值及年增速图.其中条形图表示体育产业年增加值(单位:亿元),折线图为体育产业年增长率(%).
(1)从2007年至2016年这十年中随机选出一年,求该年体育产业年增加值比前一年多500亿元以上的概率;
(2)从2007年至2011年这五年中随机选出两年,求至少有一年体育产业年增长率超过25%的概率;
(3)由图判断,从哪年开始连续三年的体育产业年增长率方差最大?从哪年开始连续三年的体育产业年增加值方差最大?(只写结论,不要求证明)
19.(12分)我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准(吨),月用水量不超过的部分按平价收费,超出的部分按议价收费.为了了解全市居民用水量的情况,通过抽样,获得了100位居民某年的月均用水量(单位:吨),将数据按照分成9组,制成了如图所示的频率分布直方图.
(1)求频率分布直方图中的值;
(2)已知该市有80万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(3)若该市政府希望使的居民每月的用水量不超过标准(吨),估计的值,并说明理由.
20.(12分)一个经销鲜花产品的微店,为保障售出的百合花品质,每天从云南鲜花基地空运固定数量的百合花,如有剩余则免费分赠给第二天购花顾客,如果不足,则从本地鲜花供应商处进货.今年四月前10天,微店百合花的售价为每枝2元,云南空运来的百合花每枝进价1.6元,本地供应商处百合花每枝进价1.8元,微店这10天的订单中百合花的日需求量(单位:枝)依次为251,255,231,243,263,241,265,255,244,252.
(1)求今年四月前10天订单中百合花日需求量的平均数和众数,并完成频率分布直方图;
(2)预计四月的后20天,订单中百合花需求量的频率分布与四月前10天相同,百合花进货价格与售价均不变,请根据(1)中频率分布直方图判断(同一组中的需求量数据用该组区间的中点值代表,位于各区间的频率代替位于该区间的概率),微店每天从云南固定空运250枝还是255枝百合花,才能使四月后20天百合花销售总利润更大?
21.(12分)2018年8月8日是我国第十个全民健身日,其主题是新时代全民健身动起来.某市为了解全民健身情况,随机从某小区居民中抽取了40人,将他们的年龄(单位:岁)分成7段:,得到如图所示的频率分布直方图.
(1)试求这40人年龄的平均数和中位数的估计值;
(2)①若从样本中年龄在的居民中任取2人赠送健身卡,求这2人中至少有1人年龄不低于60岁的概率;
②已知该小区年龄在内的总人数为2 000,若18岁以上(含18岁)为成年人,试估计该小区年龄不超过80岁的成年人人数.
22.(12分)在一次高三年级统一考试中,数学试卷有一道满分10分的选做题,学生可以从两道题目中任选一题作答.某校有900名高三学生参加了本次考试,为了了解该校学生该选做题的得分情况,计划从900名考生的选做题成绩中随机抽取一个容量为10的样本,为此将900名考生选做题的成绩按照随机顺序依次编号为001—900.
(1)若采用随机数表法抽样,并按照以下随机数表,以方框内的数字5为起点,从左向右依次读取数据,每次读取三位随机数,一行读数用完之后接下一行左端,写出样本编号的中位数;
05 26 93 70 60 22 35 85 15 13 92 03 51 59 77 59 56 78 06 83 52 91 05 70 74
07 97 10 88 23 09 98 42 99 64 61 71 62 99 15 06 5 1 29 16 93 58 05 77 09 51
51 26 87 85 85 54 87 66 47 54 73 32 08 11 12 44 95 92 63 16 29 56 24 29 48
26 99 61 65 53 58 37 78 80 70 42 10 50 67 42 32 17 55 85 74 94 44 67 16 94
14 65 52 68 75 87 59 36 22 41 26 78 63 06 55 13 08 27 01 50 15 29 39 39 43
(2)采用分层抽样的方法按照学生选择题目或题目,将成绩分为两层,且样本中题目的成绩有8个,平均数为7,方差为4;样本中题目的成绩有2个,平均数为8,方差为1.用样本估计总体,求900名考生选做题得分的平均数与方差。
第五章综合测试
答案解析
一、
1.【答案】D
【解析】概率只是说明事件发生的可能性大小,其发生具有随机性.故选D.
2.【答案】C
【解析】由题图2知,小波一星期的食品开支为300元,其中鸡蛋开支为30元,占食品开支的,而食品开支占总开支的,所以小波一星期的鸡蛋开支占总开支的百分比为.
3.【答案】C
【解析】由频率分布直方图得组距为5,故样本质量在,内的频率分别为0.3和0.5,从而中位数为,故选C.
4.【答案】B
【解析】记“取到质量小于的羽毛球”为事件A,“取到质量不小于的羽毛球”为事件B,“取到质量在范围内的羽毛球”为事件.易知事件 互斥,且为必然事件.所以,即.
5.【答案】C
【解析】由题图易得,这个月的AQI指数的变化趋势是降低的,即空气质量是变好的,所以A选项错误;前半月的AQI指数的平均数明显高于后半月,因此B、D选项错误;前半月数据的稳定性没有后半月的好,因此前半月的方差大于后半月的方差,所以C选项正确.故选C.
6.【答案】C
【解析】由茎叶图知10天中有4天空气质量为优,所以空气质量为优的频率为,所以估计该市2020年4月份空气质量为优的天数为,故选C.
7.【答案】C
【解析】由题意知,在20组随机数中表示三天中至少有两天有强浓雾的有779,588,683,569,479,978,所求概率为,故选C.
8.【答案】C
【解析】从1,2,3,4,5中任取3个不同的数共有10种不同的取法,其中的勾股数只有3,4,5,故3个数构成一组勾股数的取法只有1种,故所求概率为,故选C.
9.【答案】D
【解析】从4个阴数中随机抽取2个数,共有6种取法,其中满足题意的取法有两种:4,6和2,8.能使这两数与居中阳数之和等于15的概率.故选D.
10.【答案】D
【解析】易得,设下月每人的10工资为,则,所以的均值为,方差不变,故选D.
二、
11.【答案】ABC
【解析】甲、乙两位选手得分的茎叶图中,每个茎上的叶的数目相同,乙的所有叶上的数字之和是37,
甲的所有叶上的数字之和是,
则甲选手的平均分一定比乙选手低,则A中结论与B中结论均不正确。
甲选手得分的中位数和众数均为85,
乙选手得分的中位数和众数均为84,
则C中结论不正确,D中结论正确.故选ABC.
12.【答案】ABD
【解析】对于选项A,从图可以看出同比涨跌幅均为正数,故A正确;
对于选项B,从图可以看出环比涨跌幅有正数有负数,故B正确;
对于选项C,从图可以看出同比涨幅最大的是2018年9月份和2018年10月份,故C错误;
对于选项D,从图可以看出2019年3月全国居民消费价格环比变化最快,故D正确.
故选ABD.
三、
13.【答案】15
【解析】(人).
14.【答案】
【解析】由题意可知从甲、乙两组中各随机选取一名同学,共有9种选法,其中这两名同学的成绩相同的选法只有1种,故所求概率为.
15.【答案】
【解析】从0~9中任意取两个数(可重复)共有100种取法.若,则当甲取0或9时,乙只能猜0、1或8、9,共4种,当甲取1~8中的任一个数字时,分别有3种选择,共有24种,所以.
16.【答案】0.030 3
【解析】,
.
设身高在三组的学生分别有人,
则,解得.同理,,.
故从的学生中选取的人数为.
四、
17.【答案】(1)解:由茎叶图可知:甲班同学身高集中于之间,而乙班同学身高集中于之间.因此乙班平均身高高于甲班.
(2)解:
甲班的样本方差
(3)设“身高为的同学被抽中”为事件A,从乙班10名同学中抽取两名身高不低于的同学有,共10个基本事件,而事件A含有4个基本事件:,.
18.【答案】(1)解:设A表示事件“从2007年至2016年这十年中随机选出一年,该年体育产业年增加值比前一年多500亿元以上”根据题意,得.
(2)从2007年至2011年这五年中有两年体育产业年增长率超过,设这两年为,其他三年设为,从五年中随机选出两年,共有10种情况:
,其中至少有一年体育产业年增长率超过的有7种情况,所以所求概率为.
(3)从2008年或2009年开始连续三年的体育产业年增长率方差最大.从2014年开始连续三年的体育产业年增加值方差最大。
19.【答案】(1)解:由频率分布直方图,可得,解得.
(2)由频率分布直方图知,100位居民每人月均用水量不低于3吨的频率为.
由以上样本频率分布,可以估计全市80万居民中月均用水量不低于3吨的人数为.
(3)因为前6组的频率之和为,前5组的频率之和为,所以.
由,解得.
因此,估计月用水量标准为2.9吨时,的居民每月的用水量不超过标准.
20.【答案】(1)解:四月前10天订单中百合花日需求量的众数为255,
平均数.
补全频率分布直方图如图:
(2)设订单中百合花需求量为枝,由(1)中频率分布直方图知,的可能取值为235,245,255,265,相应频率分别为0.1,0.3,0.4,0.2,
20天中相应的天数为2、6,8,4.
①若空运250枝,则时,当日利润为(元),
时,当日利润为(元),
时,当日利润为(元),
时,当日利润为(元),
20天总利润为(元).
②若空运255枝,则
时,当日利润为(元),
时,当日利润为(元),
时,当日利润为(元),
时,当日利润为(元),
20天总利润为(元).
,每天空运250枝百合花可使四月后20天的销售总利润更大.
21.【答案】(1)解:平均数.
前三组的频率之和为,故中位数落在第3组,设中位数为,则,解得,即中位数为35.
(2)①样本中,年龄在的共有(人),其中年龄在的有4人,记为,年龄在的有2人,记为。
则从中任选2人共有如下15种情况:
.
至少有1人的年龄不低于60岁共有如下9种情况:
.
记“这2人中至少有1人年龄不低于60岁”为事件A,故所求概率.
②样本中年龄在18岁以上的居民所占频率为,
故可以估计该小区年龄不超过80岁的成年人人数为.
22.【答案】(1)解:根据题意,读出的编号依次是512,916(超界),935(超界),805,770,951(超界),512(重复),687,858,554,876,647,547,332,将有效的编号从小到大排列,得332,512,547,554,647,687,770,805,858,876.
故中位数为.
(2)解:记样本中8个A题目成绩分别为,2个B题目成绩分别为.
由题意可知,,,,
故样本平均数位,
样本方差为
.
故估计该校900名考生该选做题得分的平均数为7.2,方差为3.56.
高中数学 必修第二册 8 / 8
一、单项选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列说法正确的是( )
A.甲、乙二人比赛,甲胜的概率为,则比赛5场,甲一定会胜3场
B.某医院治疗一种疾病的治愈率为10%,前9个病人没有治愈,则第10个病人一定治愈
C.随机试验的频率与概率相等
D.天气预报中,预报明天降水概率为90%,是指明天降水的可能性是90%
2.小波一星期的总开支分布如图1所示,一星期的食品开支如图2所示,则小波一星期的鸡蛋开支占总开支的百分比为( )
图1 图2
A.1% B.2% C.3% D.5%
3.如图是容量为100的某样本的质量的频率分布直方图,则由图可估计样本质量的中位数为( )
A.11 B.11.5 C.12 D.12.5
4.从一批羽毛球中任取一个,如果取到质量小于的概率是0.3,质量不小于的概率是0.32,那么质量在范围内的概率是( )
A.0.62 B.0.38 C.0.70 D.0.68
5.空气质量指数AQI是一种反映和评价空气质量的标准,AQI指数与空气质量对应如表所示:
AQI 0~50 51~100 101~150 151~200 201~300 300以上
空气质量 优 良 轻度污染 中度污染 重度污染 严重污染
下图是某城市2018年11月全月的AQI变化统计图.
根据统计图判断,下列结论正确的是( )
A.从整体上看,这个月的空气质量越来越差
B.从整体上看,前半月的空气质量好于后半月的空气质量
C.从AQI数据看,前半月的方差大于后半月的方差
D.从AQI数据看,前半月的平均值小于后半月的平均值
6.AQI(Air Quality Index,空气质量指数)是报告每日空气质量的参数,描述了空气清洁或污染的程度.AQI共分六级:一级优(0~50);二级良(51~100);三级轻度污染(101~150);四级中度污染(151~200);五级重度污染(201~300);六级严重污染(大于300).如图是某市2019年4月份随机抽取10天的AQI指数的茎叶图,利用该样本估计该市2020年4月份空气质量为优的天数为( )
A.3 B.4 C.12 D.21
7.黄冈市的天气预报显示,大别山区在今后的三天中,一天有强浓雾的概率为40%,现用随机模拟的方法计这三天中至少有两天有强浓雾的概率:先利用计算器产生0~9之间整数值的随机数,并用0,1,2,3,4,表示没有强浓雾,用6,7,8,9表示有强浓雾,再以每个随机数作为一组,代表三天的天气情况,产生了如20组随机数:
779 537 113 730 588 506 027 394 357 231
683 569 479 812 842 273 925 191 978 520
则这三天中至少有两天有强浓雾的概率近似为( )
A. B. C. D.
8.如果3个正整数可作为一个直角三角形三条边的长,则称这3个数为一组勾股数,从1,2,3,4,5中任取3个不同的数,则这3个数构成一组勾股数的概率为( )
A. B. C. D.
9.洛书古称龟书,是阴阳五行术数之源.在古代传说中有神龟出于洛水,其甲壳上有此图像,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,五方白圈皆阳数,四隅黑点为阴数,其各行各列及对角线点数之和皆为15.如图,若从4个阴数中随机抽取2个数,则能使这2个数与居中阳数之和等于15的概率是( )
A. B. C. D.
10.某公司10位员工的月工资(单位:元)为,其均值和方差分别为和,若从下月起每位员工的月工资增加100元,则这10位员工下月工资的均值和方差分别为( )
A. B.
C. D.
二、多项选择题(本大题共2小题,每小题5分,共10分.在每小题给出的选项中,有多个选项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分)
11.如图是某电视台主办的歌手大奖赛上七位评委为甲、乙两名选手打出的分数的茎叶图(其中为数字0~9中的一个),则下列结论中不正确的是( )
A.甲选手的平均分有可能和乙选手的平均分相等
B.甲选手的平均分有可能比乙选手的平均分高
C.甲选手得分的中位数比乙选手得分的中位数低
D.甲选手得分的众数比乙选手得分的众数高
12.如图是国家统计局发布的2018年3月到2019年3月全国居民消费价格的涨跌幅情况折线图(注:2019年2月与2018年2月相比较称同比,2019年2月与2019年1月相比较称环比),根据该折线图,下列结论正确的是( )
A.2018年3月至2019年3月全国居民消费价格同比均上涨
B.2018年3月至2019年3月全国居民消费价格环比有涨有跌
C.2019年3月全国居民消费价格同比涨幅最大
D.2019年3月全国居民消费价格环比变化最快
三、填空题(本大题共4小题,每小题5分,共20分.将答案填在题中横线上)
13.某单位200名职工的年龄分布情况如图所示,现要从中抽取50名职工的年龄作为样本,若采用分层抽样方法,则40~50岁年龄段应抽取________人.
14.甲、乙两组各有三名同学,他们在一次测验中的成绩的茎叶图如图所示,如果分别从甲、乙两组中各随机选取一名同学,则这两名同学的成绩相同的概率是________.
15.甲、乙两人玩猜数字游戏,先由甲心中任想一个数字,记为,再由乙猜甲刚才想的数字,把乙猜的数字记为,且.若,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则这两人“心有灵犀”的概率为________.
16.从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).由图中数据可知________.若要从身高在三组的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在的学生中选取的人数应为________.
四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(10分)随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:),获得身高数据的茎叶图如图所示.
(1)直接根据茎叶图判断哪个班学生的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于的同学,求身高为的同学被抽中的概率.
18.(12分)改革开放40年来,体育产业的蓬勃发展反映了“健康中国”理念的普及.如图是我国2006年至2016年体育产业年增加值及年增速图.其中条形图表示体育产业年增加值(单位:亿元),折线图为体育产业年增长率(%).
(1)从2007年至2016年这十年中随机选出一年,求该年体育产业年增加值比前一年多500亿元以上的概率;
(2)从2007年至2011年这五年中随机选出两年,求至少有一年体育产业年增长率超过25%的概率;
(3)由图判断,从哪年开始连续三年的体育产业年增长率方差最大?从哪年开始连续三年的体育产业年增加值方差最大?(只写结论,不要求证明)
19.(12分)我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准(吨),月用水量不超过的部分按平价收费,超出的部分按议价收费.为了了解全市居民用水量的情况,通过抽样,获得了100位居民某年的月均用水量(单位:吨),将数据按照分成9组,制成了如图所示的频率分布直方图.
(1)求频率分布直方图中的值;
(2)已知该市有80万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(3)若该市政府希望使的居民每月的用水量不超过标准(吨),估计的值,并说明理由.
20.(12分)一个经销鲜花产品的微店,为保障售出的百合花品质,每天从云南鲜花基地空运固定数量的百合花,如有剩余则免费分赠给第二天购花顾客,如果不足,则从本地鲜花供应商处进货.今年四月前10天,微店百合花的售价为每枝2元,云南空运来的百合花每枝进价1.6元,本地供应商处百合花每枝进价1.8元,微店这10天的订单中百合花的日需求量(单位:枝)依次为251,255,231,243,263,241,265,255,244,252.
(1)求今年四月前10天订单中百合花日需求量的平均数和众数,并完成频率分布直方图;
(2)预计四月的后20天,订单中百合花需求量的频率分布与四月前10天相同,百合花进货价格与售价均不变,请根据(1)中频率分布直方图判断(同一组中的需求量数据用该组区间的中点值代表,位于各区间的频率代替位于该区间的概率),微店每天从云南固定空运250枝还是255枝百合花,才能使四月后20天百合花销售总利润更大?
21.(12分)2018年8月8日是我国第十个全民健身日,其主题是新时代全民健身动起来.某市为了解全民健身情况,随机从某小区居民中抽取了40人,将他们的年龄(单位:岁)分成7段:,得到如图所示的频率分布直方图.
(1)试求这40人年龄的平均数和中位数的估计值;
(2)①若从样本中年龄在的居民中任取2人赠送健身卡,求这2人中至少有1人年龄不低于60岁的概率;
②已知该小区年龄在内的总人数为2 000,若18岁以上(含18岁)为成年人,试估计该小区年龄不超过80岁的成年人人数.
22.(12分)在一次高三年级统一考试中,数学试卷有一道满分10分的选做题,学生可以从两道题目中任选一题作答.某校有900名高三学生参加了本次考试,为了了解该校学生该选做题的得分情况,计划从900名考生的选做题成绩中随机抽取一个容量为10的样本,为此将900名考生选做题的成绩按照随机顺序依次编号为001—900.
(1)若采用随机数表法抽样,并按照以下随机数表,以方框内的数字5为起点,从左向右依次读取数据,每次读取三位随机数,一行读数用完之后接下一行左端,写出样本编号的中位数;
05 26 93 70 60 22 35 85 15 13 92 03 51 59 77 59 56 78 06 83 52 91 05 70 74
07 97 10 88 23 09 98 42 99 64 61 71 62 99 15 06 5 1 29 16 93 58 05 77 09 51
51 26 87 85 85 54 87 66 47 54 73 32 08 11 12 44 95 92 63 16 29 56 24 29 48
26 99 61 65 53 58 37 78 80 70 42 10 50 67 42 32 17 55 85 74 94 44 67 16 94
14 65 52 68 75 87 59 36 22 41 26 78 63 06 55 13 08 27 01 50 15 29 39 39 43
(2)采用分层抽样的方法按照学生选择题目或题目,将成绩分为两层,且样本中题目的成绩有8个,平均数为7,方差为4;样本中题目的成绩有2个,平均数为8,方差为1.用样本估计总体,求900名考生选做题得分的平均数与方差。
第五章综合测试
答案解析
一、
1.【答案】D
【解析】概率只是说明事件发生的可能性大小,其发生具有随机性.故选D.
2.【答案】C
【解析】由题图2知,小波一星期的食品开支为300元,其中鸡蛋开支为30元,占食品开支的,而食品开支占总开支的,所以小波一星期的鸡蛋开支占总开支的百分比为.
3.【答案】C
【解析】由频率分布直方图得组距为5,故样本质量在,内的频率分别为0.3和0.5,从而中位数为,故选C.
4.【答案】B
【解析】记“取到质量小于的羽毛球”为事件A,“取到质量不小于的羽毛球”为事件B,“取到质量在范围内的羽毛球”为事件.易知事件 互斥,且为必然事件.所以,即.
5.【答案】C
【解析】由题图易得,这个月的AQI指数的变化趋势是降低的,即空气质量是变好的,所以A选项错误;前半月的AQI指数的平均数明显高于后半月,因此B、D选项错误;前半月数据的稳定性没有后半月的好,因此前半月的方差大于后半月的方差,所以C选项正确.故选C.
6.【答案】C
【解析】由茎叶图知10天中有4天空气质量为优,所以空气质量为优的频率为,所以估计该市2020年4月份空气质量为优的天数为,故选C.
7.【答案】C
【解析】由题意知,在20组随机数中表示三天中至少有两天有强浓雾的有779,588,683,569,479,978,所求概率为,故选C.
8.【答案】C
【解析】从1,2,3,4,5中任取3个不同的数共有10种不同的取法,其中的勾股数只有3,4,5,故3个数构成一组勾股数的取法只有1种,故所求概率为,故选C.
9.【答案】D
【解析】从4个阴数中随机抽取2个数,共有6种取法,其中满足题意的取法有两种:4,6和2,8.能使这两数与居中阳数之和等于15的概率.故选D.
10.【答案】D
【解析】易得,设下月每人的10工资为,则,所以的均值为,方差不变,故选D.
二、
11.【答案】ABC
【解析】甲、乙两位选手得分的茎叶图中,每个茎上的叶的数目相同,乙的所有叶上的数字之和是37,
甲的所有叶上的数字之和是,
则甲选手的平均分一定比乙选手低,则A中结论与B中结论均不正确。
甲选手得分的中位数和众数均为85,
乙选手得分的中位数和众数均为84,
则C中结论不正确,D中结论正确.故选ABC.
12.【答案】ABD
【解析】对于选项A,从图可以看出同比涨跌幅均为正数,故A正确;
对于选项B,从图可以看出环比涨跌幅有正数有负数,故B正确;
对于选项C,从图可以看出同比涨幅最大的是2018年9月份和2018年10月份,故C错误;
对于选项D,从图可以看出2019年3月全国居民消费价格环比变化最快,故D正确.
故选ABD.
三、
13.【答案】15
【解析】(人).
14.【答案】
【解析】由题意可知从甲、乙两组中各随机选取一名同学,共有9种选法,其中这两名同学的成绩相同的选法只有1种,故所求概率为.
15.【答案】
【解析】从0~9中任意取两个数(可重复)共有100种取法.若,则当甲取0或9时,乙只能猜0、1或8、9,共4种,当甲取1~8中的任一个数字时,分别有3种选择,共有24种,所以.
16.【答案】0.030 3
【解析】,
.
设身高在三组的学生分别有人,
则,解得.同理,,.
故从的学生中选取的人数为.
四、
17.【答案】(1)解:由茎叶图可知:甲班同学身高集中于之间,而乙班同学身高集中于之间.因此乙班平均身高高于甲班.
(2)解:
甲班的样本方差
(3)设“身高为的同学被抽中”为事件A,从乙班10名同学中抽取两名身高不低于的同学有,共10个基本事件,而事件A含有4个基本事件:,.
18.【答案】(1)解:设A表示事件“从2007年至2016年这十年中随机选出一年,该年体育产业年增加值比前一年多500亿元以上”根据题意,得.
(2)从2007年至2011年这五年中有两年体育产业年增长率超过,设这两年为,其他三年设为,从五年中随机选出两年,共有10种情况:
,其中至少有一年体育产业年增长率超过的有7种情况,所以所求概率为.
(3)从2008年或2009年开始连续三年的体育产业年增长率方差最大.从2014年开始连续三年的体育产业年增加值方差最大。
19.【答案】(1)解:由频率分布直方图,可得,解得.
(2)由频率分布直方图知,100位居民每人月均用水量不低于3吨的频率为.
由以上样本频率分布,可以估计全市80万居民中月均用水量不低于3吨的人数为.
(3)因为前6组的频率之和为,前5组的频率之和为,所以.
由,解得.
因此,估计月用水量标准为2.9吨时,的居民每月的用水量不超过标准.
20.【答案】(1)解:四月前10天订单中百合花日需求量的众数为255,
平均数.
补全频率分布直方图如图:
(2)设订单中百合花需求量为枝,由(1)中频率分布直方图知,的可能取值为235,245,255,265,相应频率分别为0.1,0.3,0.4,0.2,
20天中相应的天数为2、6,8,4.
①若空运250枝,则时,当日利润为(元),
时,当日利润为(元),
时,当日利润为(元),
时,当日利润为(元),
20天总利润为(元).
②若空运255枝,则
时,当日利润为(元),
时,当日利润为(元),
时,当日利润为(元),
时,当日利润为(元),
20天总利润为(元).
,每天空运250枝百合花可使四月后20天的销售总利润更大.
21.【答案】(1)解:平均数.
前三组的频率之和为,故中位数落在第3组,设中位数为,则,解得,即中位数为35.
(2)①样本中,年龄在的共有(人),其中年龄在的有4人,记为,年龄在的有2人,记为。
则从中任选2人共有如下15种情况:
.
至少有1人的年龄不低于60岁共有如下9种情况:
.
记“这2人中至少有1人年龄不低于60岁”为事件A,故所求概率.
②样本中年龄在18岁以上的居民所占频率为,
故可以估计该小区年龄不超过80岁的成年人人数为.
22.【答案】(1)解:根据题意,读出的编号依次是512,916(超界),935(超界),805,770,951(超界),512(重复),687,858,554,876,647,547,332,将有效的编号从小到大排列,得332,512,547,554,647,687,770,805,858,876.
故中位数为.
(2)解:记样本中8个A题目成绩分别为,2个B题目成绩分别为.
由题意可知,,,,
故样本平均数位,
样本方差为
.
故估计该校900名考生该选做题得分的平均数为7.2,方差为3.56.
高中数学 必修第二册 8 / 8
