苏科版八年级下册数学9.4 矩形、菱形、正方形-矩形教案
文档属性
| 名称 | 苏科版八年级下册数学9.4 矩形、菱形、正方形-矩形教案 |  | |
| 格式 | zip | ||
| 文件大小 | 170.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-26 08:51:40 | ||
图片预览

文档简介
9.4 矩形(1)
教学目标
1.知识与技能
理解矩形的概念,以及平行四边形与矩形之间的关系。
2.过程与方法
经历操作、探索、猜想、并证明矩形的性质定理的过程,进一步理解对猜想进行证明的必要性,同时体会类比学习思想的重要性。
3.情感态度与价值观
在对矩形的性质探索过程中,理解特殊与一般的关系,领会特殊事物的本质属性与其特殊性质的关系。
教学重点
矩形特殊性质的探索及证明
教学难点
提出某些命题(或问题)并证明它的正确性
教学方法
自主和类比学习,合作探究,归纳总结
教学过程
课前2min完成平行四边形的相关知识内容.
1、【感知图形,归纳概念】
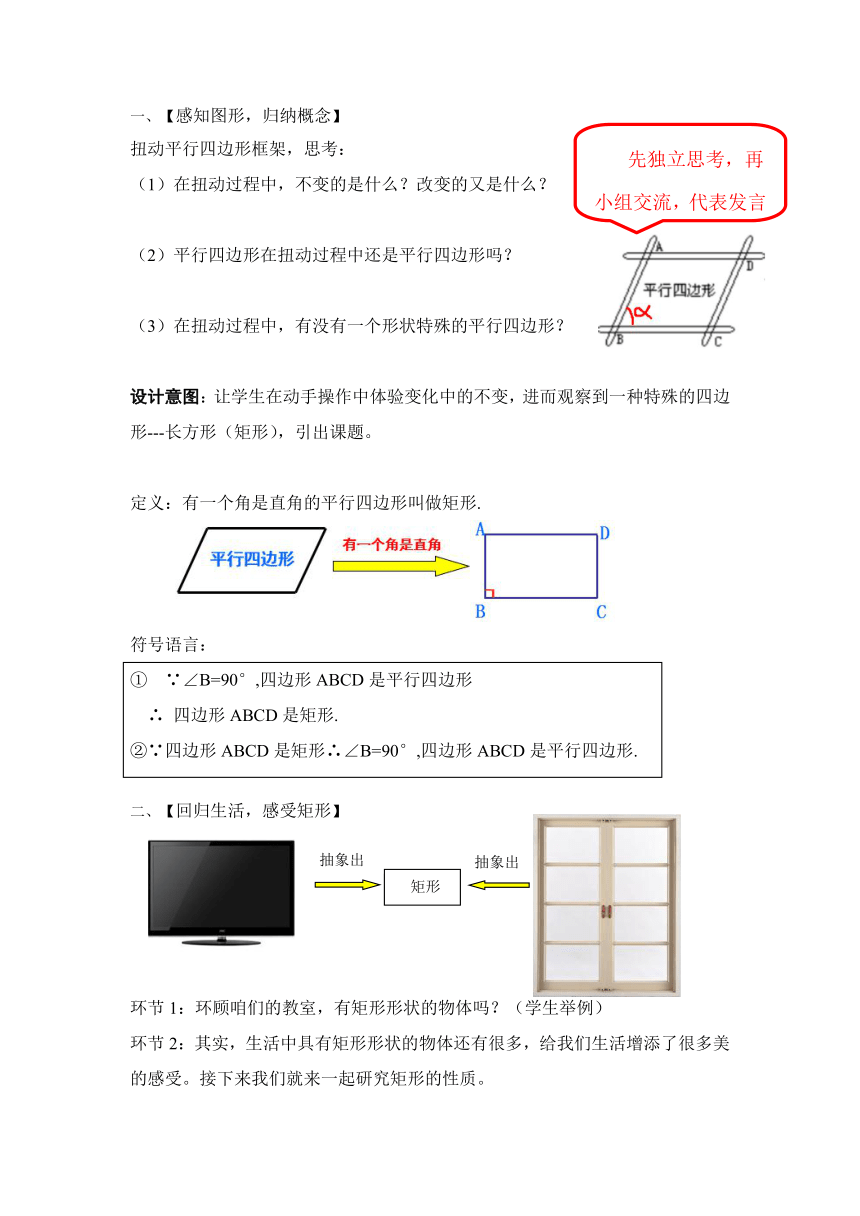
扭动平行四边形框架,思考:
(1)在扭动过程中,不变的是什么?改变的又是什么?
(2)平行四边形在扭动过程中还是平行四边形吗?
(3)在扭动过程中,有没有一个形状特殊的平行四边形?
设计意图:让学生在动手操作中体验变化中的不变,进而观察到一种特殊的四边形---长方形(矩形),引出课题。
定义:有一个角是直角的平行四边形叫做矩形.
符号语言:
① ∵∠B=90°,四边形ABCD是平行四边形
∴ 四边形ABCD是矩形.
②∵四边形ABCD是矩形∴∠B=90°,四边形ABCD是平行四边形.
2、【回归生活,感受矩形】
环节1:环顾咱们的教室,有矩形形状的物体吗?(学生举例)
环节2:其实,生活中具有矩形形状的物体还有很多,给我们生活增添了很多美的感受。接下来我们就来一起研究矩形的性质。
3、【动手操作, 探索性质】
拿出矩形纸片,类比平行四边形性质的探索方法,思考:
(1)矩形ABCD除了具备平行四边形的性质外,还有哪些特殊的性质?
(2)你还有哪些发现?
四、【小组合作,证明性质】
1.如图,四边形ABCD是矩形.
求证:∠A=∠B=∠C=∠D=90°
证明:∵四边形ABCD是矩形
∴∠B=90°
又∵矩形ABCD是平行四边形
∴∠B=∠D,∠A=∠C
∠A+∠B=180°
∴∠A=∠B=∠C=∠D=90°即矩形的四个角都是直角
2.如图,矩形ABCD的对角线AC、BD相交于点O.求证:AC=BD.
证明:∵四边形ABCD是矩形
∴∠ABC=∠DCB=90°
AB=DC,BC=CB
∴△ABC≌△DCB
∴AC=BD
即矩形的对角线相等
设计意图:让学生经历操作、猜想、最后再证明从而得到矩形的性质定理,这一系列过程就是我们用数学的眼光研究问题的一般方法,学生的逻辑思维表达能力也得到提升。
五、【简单应用】
例题:已知:如图,矩形ABCD的两条对角线相交于点O,且AC=2AB.求证:△AOB是等边三角形.
(变式1)已知:如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°
(1)判断△AOB的形状,并说明理由;
(2)若AB = 1cm, 矩形对角线AC的长和BC边的长.
(变式2)已知:如图,矩形ABCD的两条对角线相交于点O,且CE∥DB,交AB的延长线于点E, 请尝试提出一个有价值的问题.
设计意图:
(1)熟悉和应用矩形的有关性质;(2)引导学生在讨论、交流中体会分析和综合的思考方法;(3)矩形问题常常与等腰三角形(或等边三角形)、直角三角形(勾股定理)有关;(4)变式2是一个开放问题,让不同层次的同学都能提出相应有价值的问题,并尝试去解决问题。学生的提出的问题与问题之间可能存在着某种递进关系,可以尝试问问学生:哪个你最容易解决?其次会做哪个?让不同层次的同学在问题的解决中体验不同的快乐。
六、【小结反思】
1.通过本节课的学习,你有哪些收获?还有哪些疑问?
2.你觉得后面我们会研究什么?用什么方法研究?
7、【作业】
1、完善课堂学案;
2、课本第83页第4题。
先独立思考,再小组交流,代表发言
抽象出
矩形
抽象出
先独立思考,再小组交流,代表发言
符号语言
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=90°
符号语言
∵四边形ABCD是矩形
∴ AC=BD
教学目标
1.知识与技能
理解矩形的概念,以及平行四边形与矩形之间的关系。
2.过程与方法
经历操作、探索、猜想、并证明矩形的性质定理的过程,进一步理解对猜想进行证明的必要性,同时体会类比学习思想的重要性。
3.情感态度与价值观
在对矩形的性质探索过程中,理解特殊与一般的关系,领会特殊事物的本质属性与其特殊性质的关系。
教学重点
矩形特殊性质的探索及证明
教学难点
提出某些命题(或问题)并证明它的正确性
教学方法
自主和类比学习,合作探究,归纳总结
教学过程
课前2min完成平行四边形的相关知识内容.
1、【感知图形,归纳概念】
扭动平行四边形框架,思考:
(1)在扭动过程中,不变的是什么?改变的又是什么?
(2)平行四边形在扭动过程中还是平行四边形吗?
(3)在扭动过程中,有没有一个形状特殊的平行四边形?
设计意图:让学生在动手操作中体验变化中的不变,进而观察到一种特殊的四边形---长方形(矩形),引出课题。
定义:有一个角是直角的平行四边形叫做矩形.
符号语言:
① ∵∠B=90°,四边形ABCD是平行四边形
∴ 四边形ABCD是矩形.
②∵四边形ABCD是矩形∴∠B=90°,四边形ABCD是平行四边形.
2、【回归生活,感受矩形】
环节1:环顾咱们的教室,有矩形形状的物体吗?(学生举例)
环节2:其实,生活中具有矩形形状的物体还有很多,给我们生活增添了很多美的感受。接下来我们就来一起研究矩形的性质。
3、【动手操作, 探索性质】
拿出矩形纸片,类比平行四边形性质的探索方法,思考:
(1)矩形ABCD除了具备平行四边形的性质外,还有哪些特殊的性质?
(2)你还有哪些发现?
四、【小组合作,证明性质】
1.如图,四边形ABCD是矩形.
求证:∠A=∠B=∠C=∠D=90°
证明:∵四边形ABCD是矩形
∴∠B=90°
又∵矩形ABCD是平行四边形
∴∠B=∠D,∠A=∠C
∠A+∠B=180°
∴∠A=∠B=∠C=∠D=90°即矩形的四个角都是直角
2.如图,矩形ABCD的对角线AC、BD相交于点O.求证:AC=BD.
证明:∵四边形ABCD是矩形
∴∠ABC=∠DCB=90°
AB=DC,BC=CB
∴△ABC≌△DCB
∴AC=BD
即矩形的对角线相等
设计意图:让学生经历操作、猜想、最后再证明从而得到矩形的性质定理,这一系列过程就是我们用数学的眼光研究问题的一般方法,学生的逻辑思维表达能力也得到提升。
五、【简单应用】
例题:已知:如图,矩形ABCD的两条对角线相交于点O,且AC=2AB.求证:△AOB是等边三角形.
(变式1)已知:如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°
(1)判断△AOB的形状,并说明理由;
(2)若AB = 1cm, 矩形对角线AC的长和BC边的长.
(变式2)已知:如图,矩形ABCD的两条对角线相交于点O,且CE∥DB,交AB的延长线于点E, 请尝试提出一个有价值的问题.
设计意图:
(1)熟悉和应用矩形的有关性质;(2)引导学生在讨论、交流中体会分析和综合的思考方法;(3)矩形问题常常与等腰三角形(或等边三角形)、直角三角形(勾股定理)有关;(4)变式2是一个开放问题,让不同层次的同学都能提出相应有价值的问题,并尝试去解决问题。学生的提出的问题与问题之间可能存在着某种递进关系,可以尝试问问学生:哪个你最容易解决?其次会做哪个?让不同层次的同学在问题的解决中体验不同的快乐。
六、【小结反思】
1.通过本节课的学习,你有哪些收获?还有哪些疑问?
2.你觉得后面我们会研究什么?用什么方法研究?
7、【作业】
1、完善课堂学案;
2、课本第83页第4题。
先独立思考,再小组交流,代表发言
抽象出
矩形
抽象出
先独立思考,再小组交流,代表发言
符号语言
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=90°
符号语言
∵四边形ABCD是矩形
∴ AC=BD
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
