华师大版九年级下册数学27.2.3切线长定理课件(29张)
文档属性
| 名称 | 华师大版九年级下册数学27.2.3切线长定理课件(29张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-26 00:00:00 | ||
图片预览



文档简介
(共29张PPT)
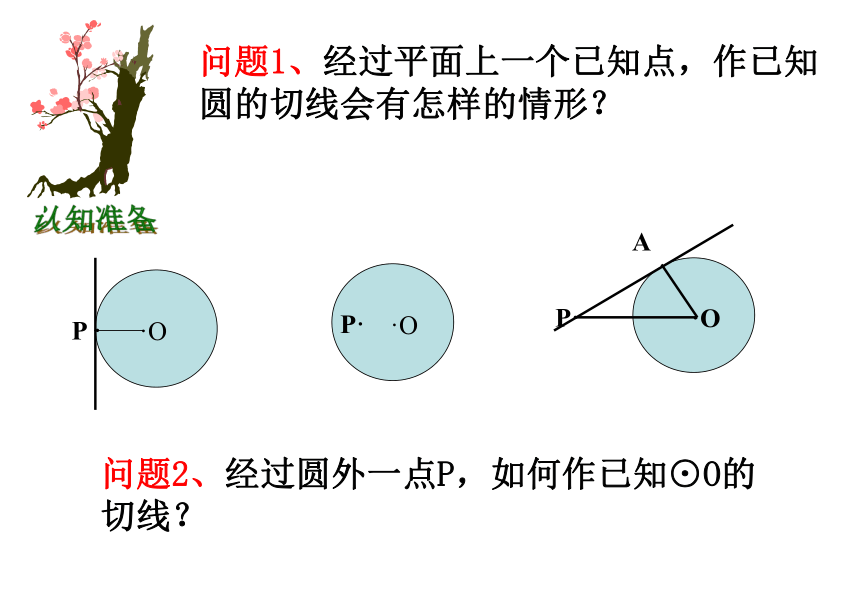
问题1、经过平面上一个已知点,作已知圆的切线会有怎样的情形?
P ·
P·
P·
问题2、经过圆外一点P,如何作已知⊙O的
切线?
O
。
A
B
P
思考:假设切线PA已作出,A为切点,则∠OAP=90°,连接OP,可知点A在怎样的圆上?
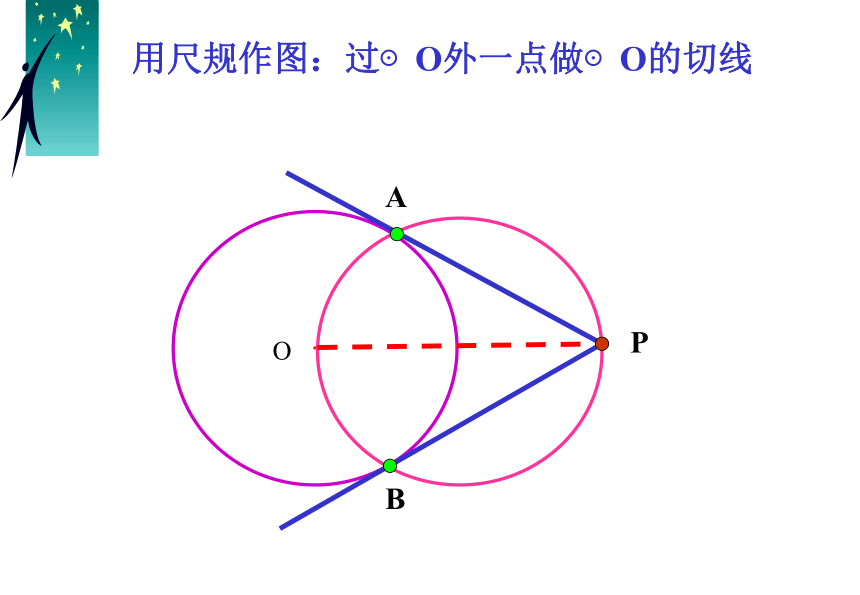
用尺规作图:过⊙O外一点做⊙O的切线
O
·
P
A
B
O
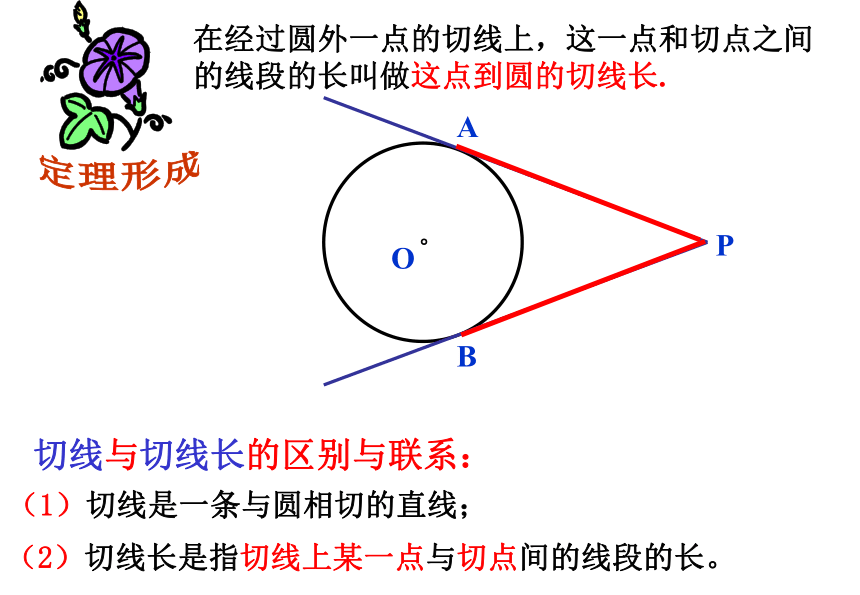
在经过圆外一点的切线上,这一点和切点之间的线段的长叫做这点到圆的切线长.
切线与切线长的区别与联系:
(1)切线是一条与圆相切的直线;
(2)切线长是指切线上某一点与切点间的线段的长。
。
P
B
A
O
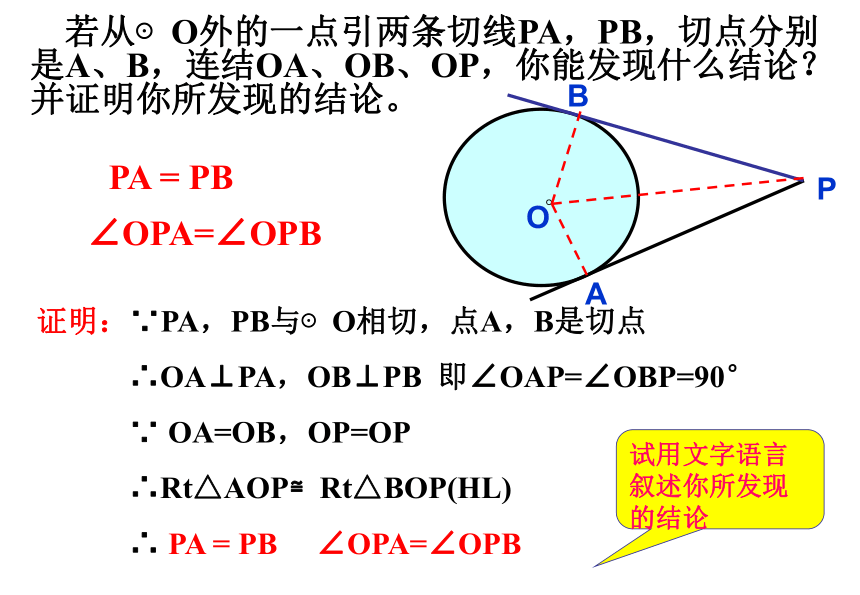
若从⊙O外的一点引两条切线PA,PB,切点分别是A、B,连结OA、OB、OP,你能发现什么结论?并证明你所发现的结论。
PA = PB
∠OPA=∠OPB
证明:∵PA,PB与⊙O相切,点A,B是切点
∴OA⊥PA,OB⊥PB 即∠OAP=∠OBP=90°
∵ OA=OB,OP=OP
∴Rt△AOP≌Rt△BOP(HL)
∴ PA = PB ∠OPA=∠OPB
试用文字语言叙述你所发现的结论
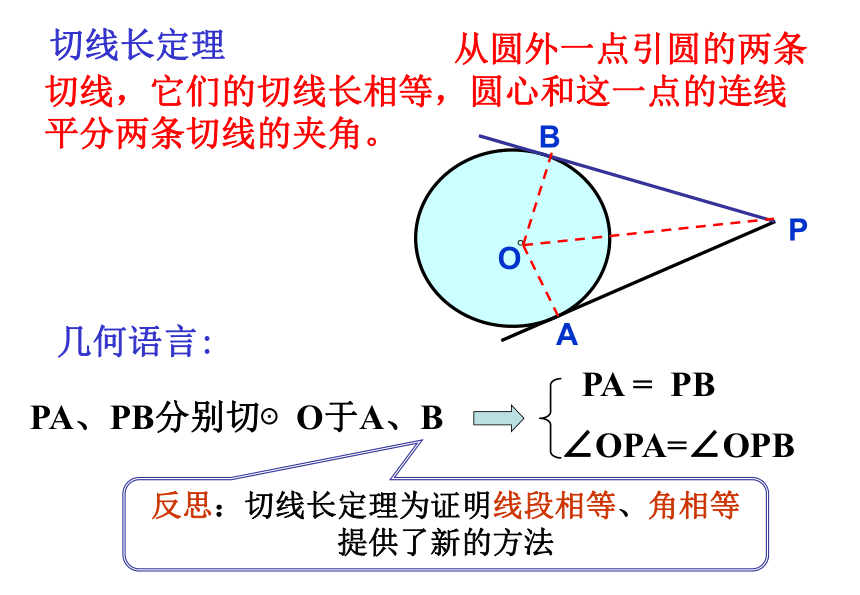
PA、PB分别切⊙O于A、B
PA = PB
∠OPA=∠OPB
从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
切线长定理
几何语言:
反思:切线长定理为证明线段相等、角相等提供了新的方法
A
P
O
。
B
若连结两切点A、B,AB交OP于点M.你又能得出什么新的结论?并给出证明.
OP垂直平分AB
证明:∵PA,PB是⊙O的切线,点A,B是切点
∴PA = PB ∠OPA=∠OPB
∴△PAB是等腰三角形,PM为顶角的平分线
∴OP垂直平分AB
A
P
O
。
B
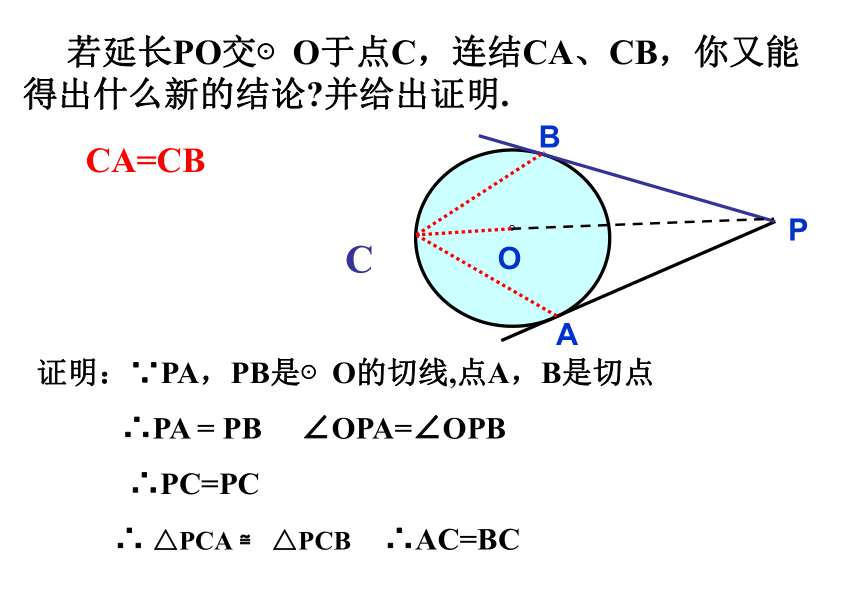
若延长PO交⊙O于点C,连结CA、CB,你又能得出什么新的结论?并给出证明.
CA=CB
证明:∵PA,PB是⊙O的切线,点A,B是切点
∴PA = PB ∠OPA=∠OPB
∴PC=PC
∴ △PCA ≌ △PCB ∴AC=BC
C
(1)写出图中所有的垂直关系
OA⊥PA,OB ⊥PB,AB ⊥OP
(3)写出图中所有的全等三角形
△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP
(4)写出图中所有的相似三角形
△AOC∽ △BOC∽ △AOP∽△BOP∽ △ACP∽BCP
(5)写出图中所有的等腰三角形
△ABP △AOB
(6)若PA=4、PD=2,求半径OA
(2)写出图中与∠OAC相等的角
∠OAC=∠OBC=∠APC=∠BPC
。
P
B
A
O
(3)连结圆心和圆外一点
(2)连结两切点
(1)分别连结圆心和切点
在解决有关圆的切线长问题时,往往需要我们构建基本图形。
如图,已知⊙O的半径为3cm.点P和圆心O的距离为6cm,经过点P有⊙O的两条切线PA 、 PB,则切线长为_____cm,这两条切线的夹角为______, ∠ AOB=______。
60 °
120 °
例1: 如图,已知AB、AC是⊙O的切线,B、C为
切点,连结BC交AO于D.
⑴若AD=6,AO=8,求切线AB的长;
⑵若BC=4,∠BAO=30°,求⊙O的直径。
小红为了测量一个锅盖的直径,她用了下面的方法:将锅盖平放在水平桌上,用一个锐角为300的三角板和一个刻度尺,按如图所示的方法得到相关的数据,测得PA=10cm,即求出锅盖的直径.
说明她这样做的理由.
┐
如图:用两根带有刻度的木条做一个夹角为60°的
工具尺,你能用它量出一个圆的半径吗?
若量出角的顶点到切点的距离为10cm,试求这个圆
半径的近似值。
例2: 已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为AB上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=12CM,∠P=50°.
求:(1)△PEF的周长; (2) ∠EOF的度数.
E
A
Q
P
F
B
O
如图,从⊙O外一点P作⊙O的两条切线,分别切⊙O于A 、B,在AB上任取一点C作⊙O的切线分别交PA 、PB于D 、E
(1)若PA=2,则△PDE的周长为____;若PA=a,则△PDE的周长为_____。
(2)连结OD 、OE,若∠P=40 °,则
∠DOE=_____;若∠P=k度,∠DOE=__________ 度 。
E
· O
C
B
D
P
A
4
2a
70 °
小红家院子有一块三角形草坪, 她想在这块地里设计一个最大的圆形花坛,你能帮她设计一下吗?
与三角形各边都相切的圆叫做三角形
的内切圆
三角形的内切圆的圆心叫做
三角形的内心
这个三角形叫做圆的
外切三角形
三角形的内心就是三角形三条
内角平分线的交点
一处
两处
三处
四处
直线l1、l2、l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
D
例3: (1) 在△ABC中,∠ABC =500, ∠ACB=750, 点O是△ABC的内心, 求∠BOC的度数.
(2) 在△ABC中, ∠BAC=550, 点O是△ABC的内心, 求∠BOC的度数 .
例4:如图, △ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=9cm, BC=14cm,CA=13cm,求AF、BD、CE的长。
x
13﹣x
x
13﹣x
9﹣x
9﹣x
y
z
y
z
x+y=9
y+z=14
x+z=13
(13﹣x)+(9﹣x)=14
设△ABC的BC=a,AC=b,AB=c,内切圆I和BC、AC、AB分别相切于点D、E、F,求AE、BD、CE的长.
.
I
x
y
z
y+z=a
x+z=b
x+y=c
分析:设 AF=x,BD=y,CE=z
.I
x
y
z
.
CD值怎样? r ?
已知:一块三角形的白铁片,量得三边的长分别为5cm , 12cm, 13com.从这块白铁片上能剪下最大的圆的半径是多少长? 。
例5:△ABC的内切圆半径为 r , △ABC的周长为 l ,求△ABC的面积。
(提示:设内心为O,连接OA、OB、OC。)
r
r
r
如图,⊙O内切于△ABC,D、E、F分别是切点,若⊙O的半径为 ,∠C=60o,AC=9,BC=14,求△ABC的周长.
答案:40
1.切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
∵PA、PB分别切⊙O于A、B
∴PA = PB ,∠OPA=∠OPB
OP垂直平分AB
切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了理论依据。必须掌握并能灵活应用。
2.你还有什么收获吗?
O
O
C
B
A
c
b
a
问题1、经过平面上一个已知点,作已知圆的切线会有怎样的情形?
P ·
P·
P·
问题2、经过圆外一点P,如何作已知⊙O的
切线?
O
。
A
B
P
思考:假设切线PA已作出,A为切点,则∠OAP=90°,连接OP,可知点A在怎样的圆上?
用尺规作图:过⊙O外一点做⊙O的切线
O
·
P
A
B
O
在经过圆外一点的切线上,这一点和切点之间的线段的长叫做这点到圆的切线长.
切线与切线长的区别与联系:
(1)切线是一条与圆相切的直线;
(2)切线长是指切线上某一点与切点间的线段的长。
。
P
B
A
O
若从⊙O外的一点引两条切线PA,PB,切点分别是A、B,连结OA、OB、OP,你能发现什么结论?并证明你所发现的结论。
PA = PB
∠OPA=∠OPB
证明:∵PA,PB与⊙O相切,点A,B是切点
∴OA⊥PA,OB⊥PB 即∠OAP=∠OBP=90°
∵ OA=OB,OP=OP
∴Rt△AOP≌Rt△BOP(HL)
∴ PA = PB ∠OPA=∠OPB
试用文字语言叙述你所发现的结论
PA、PB分别切⊙O于A、B
PA = PB
∠OPA=∠OPB
从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
切线长定理
几何语言:
反思:切线长定理为证明线段相等、角相等提供了新的方法
A
P
O
。
B
若连结两切点A、B,AB交OP于点M.你又能得出什么新的结论?并给出证明.
OP垂直平分AB
证明:∵PA,PB是⊙O的切线,点A,B是切点
∴PA = PB ∠OPA=∠OPB
∴△PAB是等腰三角形,PM为顶角的平分线
∴OP垂直平分AB
A
P
O
。
B
若延长PO交⊙O于点C,连结CA、CB,你又能得出什么新的结论?并给出证明.
CA=CB
证明:∵PA,PB是⊙O的切线,点A,B是切点
∴PA = PB ∠OPA=∠OPB
∴PC=PC
∴ △PCA ≌ △PCB ∴AC=BC
C
(1)写出图中所有的垂直关系
OA⊥PA,OB ⊥PB,AB ⊥OP
(3)写出图中所有的全等三角形
△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP
(4)写出图中所有的相似三角形
△AOC∽ △BOC∽ △AOP∽△BOP∽ △ACP∽BCP
(5)写出图中所有的等腰三角形
△ABP △AOB
(6)若PA=4、PD=2,求半径OA
(2)写出图中与∠OAC相等的角
∠OAC=∠OBC=∠APC=∠BPC
。
P
B
A
O
(3)连结圆心和圆外一点
(2)连结两切点
(1)分别连结圆心和切点
在解决有关圆的切线长问题时,往往需要我们构建基本图形。
如图,已知⊙O的半径为3cm.点P和圆心O的距离为6cm,经过点P有⊙O的两条切线PA 、 PB,则切线长为_____cm,这两条切线的夹角为______, ∠ AOB=______。
60 °
120 °
例1: 如图,已知AB、AC是⊙O的切线,B、C为
切点,连结BC交AO于D.
⑴若AD=6,AO=8,求切线AB的长;
⑵若BC=4,∠BAO=30°,求⊙O的直径。
小红为了测量一个锅盖的直径,她用了下面的方法:将锅盖平放在水平桌上,用一个锐角为300的三角板和一个刻度尺,按如图所示的方法得到相关的数据,测得PA=10cm,即求出锅盖的直径.
说明她这样做的理由.
┐
如图:用两根带有刻度的木条做一个夹角为60°的
工具尺,你能用它量出一个圆的半径吗?
若量出角的顶点到切点的距离为10cm,试求这个圆
半径的近似值。
例2: 已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为AB上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=12CM,∠P=50°.
求:(1)△PEF的周长; (2) ∠EOF的度数.
E
A
Q
P
F
B
O
如图,从⊙O外一点P作⊙O的两条切线,分别切⊙O于A 、B,在AB上任取一点C作⊙O的切线分别交PA 、PB于D 、E
(1)若PA=2,则△PDE的周长为____;若PA=a,则△PDE的周长为_____。
(2)连结OD 、OE,若∠P=40 °,则
∠DOE=_____;若∠P=k度,∠DOE=__________ 度 。
E
· O
C
B
D
P
A
4
2a
70 °
小红家院子有一块三角形草坪, 她想在这块地里设计一个最大的圆形花坛,你能帮她设计一下吗?
与三角形各边都相切的圆叫做三角形
的内切圆
三角形的内切圆的圆心叫做
三角形的内心
这个三角形叫做圆的
外切三角形
三角形的内心就是三角形三条
内角平分线的交点
一处
两处
三处
四处
直线l1、l2、l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
D
例3: (1) 在△ABC中,∠ABC =500, ∠ACB=750, 点O是△ABC的内心, 求∠BOC的度数.
(2) 在△ABC中, ∠BAC=550, 点O是△ABC的内心, 求∠BOC的度数 .
例4:如图, △ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=9cm, BC=14cm,CA=13cm,求AF、BD、CE的长。
x
13﹣x
x
13﹣x
9﹣x
9﹣x
y
z
y
z
x+y=9
y+z=14
x+z=13
(13﹣x)+(9﹣x)=14
设△ABC的BC=a,AC=b,AB=c,内切圆I和BC、AC、AB分别相切于点D、E、F,求AE、BD、CE的长.
.
I
x
y
z
y+z=a
x+z=b
x+y=c
分析:设 AF=x,BD=y,CE=z
.I
x
y
z
.
CD值怎样? r ?
已知:一块三角形的白铁片,量得三边的长分别为5cm , 12cm, 13com.从这块白铁片上能剪下最大的圆的半径是多少长? 。
例5:△ABC的内切圆半径为 r , △ABC的周长为 l ,求△ABC的面积。
(提示:设内心为O,连接OA、OB、OC。)
r
r
r
如图,⊙O内切于△ABC,D、E、F分别是切点,若⊙O的半径为 ,∠C=60o,AC=9,BC=14,求△ABC的周长.
答案:40
1.切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
∵PA、PB分别切⊙O于A、B
∴PA = PB ,∠OPA=∠OPB
OP垂直平分AB
切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了理论依据。必须掌握并能灵活应用。
2.你还有什么收获吗?
O
O
C
B
A
c
b
a
