人教版七年级数学下册课件: 6.3 实数(37张ppt)
文档属性
| 名称 | 人教版七年级数学下册课件: 6.3 实数(37张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-25 10:53:37 | ||
图片预览






文档简介
(共37张PPT)
6.3 实数
6
实数
课时目标
1.了解实数的概念,会按两种方式将实数分类,会在实数范围内求相反数、绝对值,会进行简单的实数运算。
2.了解分类的标准与分类的结果的相关性,进一步了解体会“集合”的含义。
3.经历无限不循环小数与有限小数、无限循环小数的对比过程,进一步理解什么是无限不循环小数,从而知道什么是无理数。
探究新知
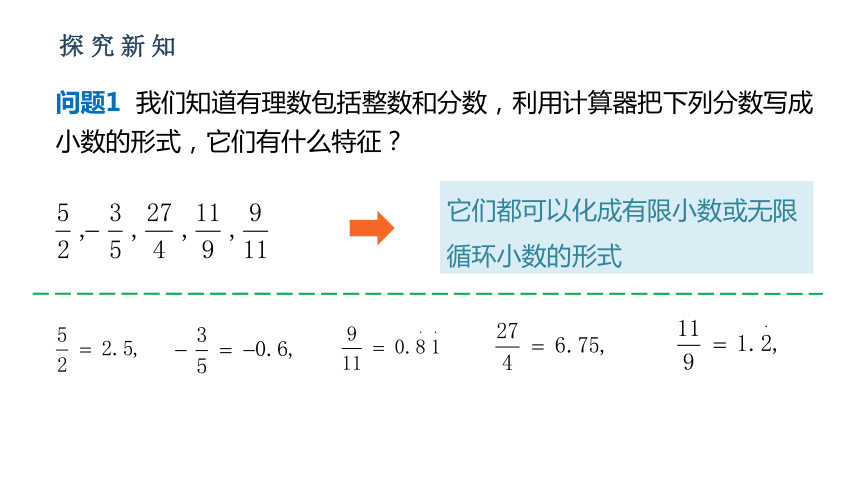
问题1 我们知道有理数包括整数和分数,利用计算器把下列分数写成小数的形式,它们有什么特征?
它们都可以化成有限小数或无限循环小数的形式
探究新知
问题2 整数能写成小数的形式吗?3 可以看成是 3.0 吗?
可以
思考 由此你可以得到什么结论?
有理数都可以化成有限小数或无限循环小数的形式.
反过来,任何有限小数或无限循环小数也都是有理数.
探究新知
叫做无理数.
想一想:所有的数都可以写成 有限小数 和 无限循环小数 的形式吗?
1.01001000100001…
(两个1之间依次多一个0)
无限不循环小数
不是 如:
探究新知
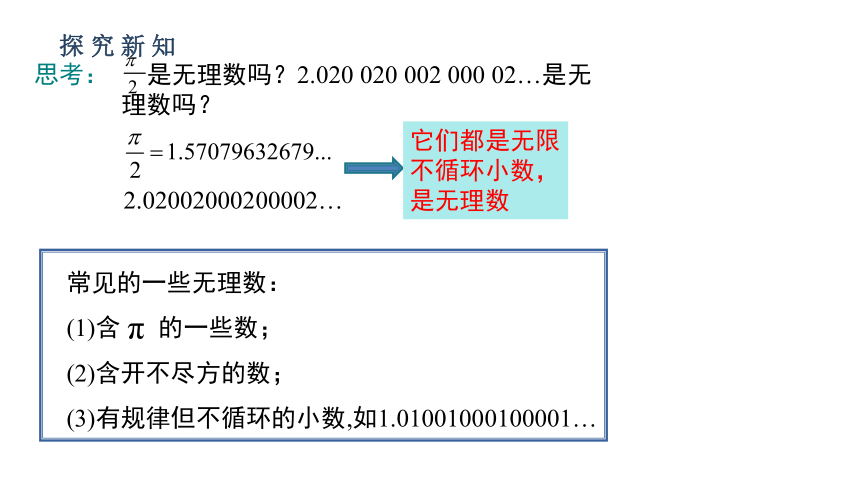
思考: 是无理数吗?2.020 020 002 000 02…是无
理数吗?
2.02002000200002…
常见的一些无理数:
(1)含 的一些数;
(2)含开不尽方的数;
(3)有规律但不循环的小数,如1.01001000100001…
它们都是无限不循环小数,是无理数
探究新知
把下列各数分别填入相应的集合内:
0.101,
有理数集合
无理数集合
...
...
探究新知
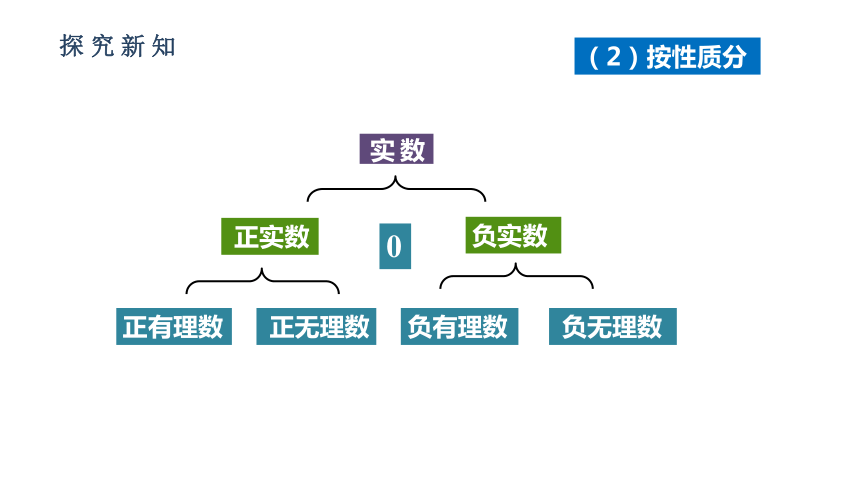
负实数
正实数
数实
正有理数
负有理数
(2)按性质分
0
正无理数
负无理数
探究新知
无理数:
有理数:
负实数:
正实数:
例1 将下列各数分别填入下列相应的括号内:
对每个数都要进行判断,分类标准不同结果不同.
探究新知
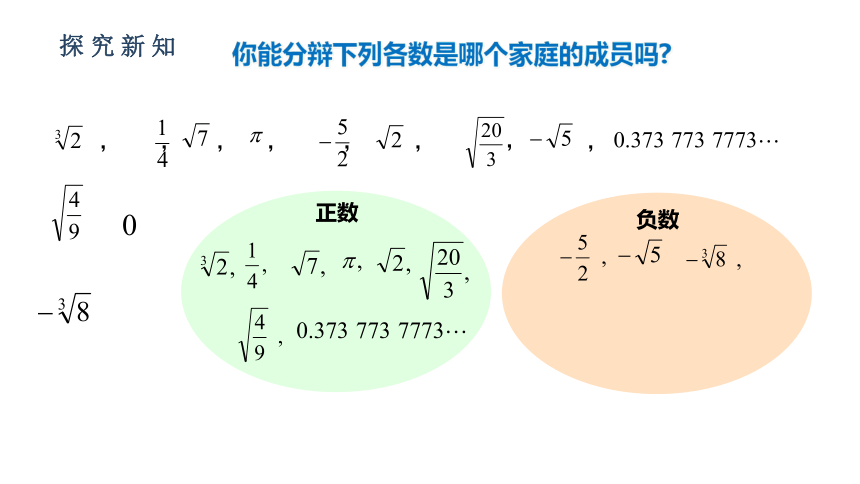
你能分辩下列各数是哪个家庭的成员吗?
,
,
,
,
,
,
,
,
正数
负数
探究新知
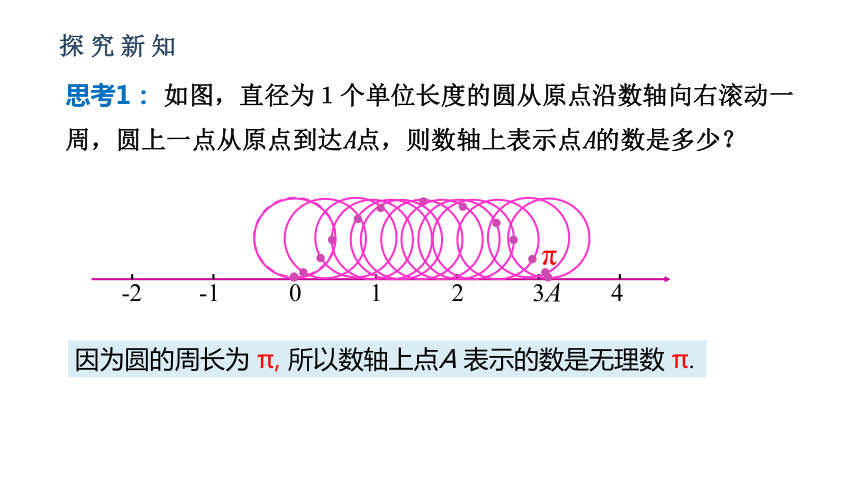
思考1: 如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达A点,则数轴上表示点A的数是多少?
因为圆的周长为 π, 所以数轴上点A 表示的数是无理数 π.
0
-2
-1
1
3
2
4
●
●
●
●
●
●
●
●
●
●
●
●
●
●
A
巩固练习
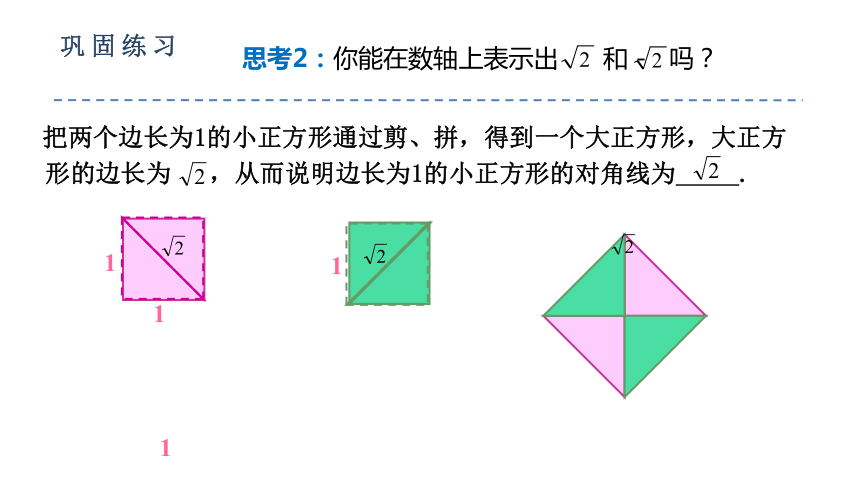
思考2:你能在数轴上表示出 和 - 吗?
1
1
1
1
把两个边长为1的小正方形通过剪、拼,得到一个大正方形,大正方形的边长为 ,从而说明边长为1的小正方形的对角线为 .
巩固练习
-2
-1
0
1
2
-
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一点都表示一个实数.
★ 实数和数轴上的点是 一 一对应的.
巩固练习
例2:如图所示,数轴上A,B两点表示的数分别为-1和 ,点B关于点A的对称点为C,求点C所表示的实数.
解:∵数轴上A,B两点表示的数分别为-1和 ,
∴点B到点A的距离为1+ ,则点C到点A的距离为1+ ,
设点C表示的实数为x,则点A到点C的距离为-1-x,
∴-1-x=1+ ,
∴x=-2-
巩固练习
例3 如图所示,数轴上A,B两点表示的数分别为 和5.1,则A,B两点之间表示整数的点共有( )
A.6个 B.5个 C.4个 D.3个
C
巩固练习
解析:∵ ≈1.414,∴ 和5.1之间的整数有2,3,4,5, ∴A,B两点之间表示整数的点共有4个.
【方法总结】数轴上的点与实数一一对应,结合数轴分析,可轻松得出结论.
巩固练习
与有理数一样,实数也可以比较大小:
实数的大小比较
与有理数规定的大小一样,数轴上右边的点表示的实数比左边的点表示的实数大.
原点
0
正实数
负实数
<
巩固练习
1.正数大于零,负数小于零,正数大于负数;
2.两个正数,绝对值大的数较大;
3.两个负数,绝对值大的数反而小.
与有理数一样,在实数范围内:
巩固练习
,2可以分别看作是面积为5,4的正方形的边长,容易说明:面积较大的正方形,它的边长也较大,因此
同样,因为5<9,所以
不用计算器, 与2比较哪个大?与3比较呢?
巩固练习
例4 在数轴上表示下列各点,比较它们的大小,并用“<”连接它们.
-2 -1 0 1 2 3
1
-2
-2< < 1< <
例5 估计 位于( )
A.0~1之间 B.1~2之间 C.2~3之间 D.3~4之间
B
巩固练习
例6 比较下列各组数的大小:
解 : (1)因为 12 < 42,
所以 < 4,
所以 -1< 3;
(2)因为 10 > 32 ,
所以
所以
巩固练习
A. a 一定是正实数
B. 是有理数
C. 是有理数
D.数轴上任一点都对应一个有理数
B
1. 下列说法正确的是( )
巩固练习
2.有一个数值转换器,原理如下,当输x =81时,输出的y 是 ( )
A.9 B.3 C. D.±3
C
巩固练习
3. 判断快枪手 —— 看谁最快最准
(1)实数不是有理数就是无理数. ( )
(2)无理数都是无限不循环小数. ( )
(4)无理数都是无限小数. ( )
(3)带根号的数都是无理数. ( )
(5)无理数一定都带根号. ( )
×
×
巩固练习
4. 比较 与 6 的大小.
解: ∵37 >36
∴ > 6.
巩固练习
1.交换律 : 加法 a+b=b+a
乘法a×b=b×a
2.结合律: 加法(a+b)+c=a+(b+c)
乘法(a×b)×c=a×(b×c)
3.分配律: a× (b+c)= a×b+ a×c
注:有理数的运算律和运算法则在实数范围内同样适用
总结有理数的运算律和运算法则
巩固练习
实数的相反数、绝对值、倒数
相反数:
实数 a 的相反数是- a.若a与b互为相反数,则a+b=0.
绝对值:
实数a的绝对值,记为|a|,它是一个非负实数.
|a| =
a( a﹥0 )
0 ( a = 0)
-a( a﹤0)
几何意义: |a|表示点到原点0的距离.而| a-b |表示数a表示的点到数b表示的点的距离.
巩固练习
习题 6.3
巩固练习
巩固练习
巩固练习
巩固练习
巩固练习
巩固练习
巩固练习
巩固练习
1.无限不循环小数叫做无理数。
2.有理数和无理数统称实数。
3.实数按定义分类为有理数和无理数;按正负分类为正实数、0和负实数.
课堂小结
6.3 实数
6
实数
课时目标
1.了解实数的概念,会按两种方式将实数分类,会在实数范围内求相反数、绝对值,会进行简单的实数运算。
2.了解分类的标准与分类的结果的相关性,进一步了解体会“集合”的含义。
3.经历无限不循环小数与有限小数、无限循环小数的对比过程,进一步理解什么是无限不循环小数,从而知道什么是无理数。
探究新知
问题1 我们知道有理数包括整数和分数,利用计算器把下列分数写成小数的形式,它们有什么特征?
它们都可以化成有限小数或无限循环小数的形式
探究新知
问题2 整数能写成小数的形式吗?3 可以看成是 3.0 吗?
可以
思考 由此你可以得到什么结论?
有理数都可以化成有限小数或无限循环小数的形式.
反过来,任何有限小数或无限循环小数也都是有理数.
探究新知
叫做无理数.
想一想:所有的数都可以写成 有限小数 和 无限循环小数 的形式吗?
1.01001000100001…
(两个1之间依次多一个0)
无限不循环小数
不是 如:
探究新知
思考: 是无理数吗?2.020 020 002 000 02…是无
理数吗?
2.02002000200002…
常见的一些无理数:
(1)含 的一些数;
(2)含开不尽方的数;
(3)有规律但不循环的小数,如1.01001000100001…
它们都是无限不循环小数,是无理数
探究新知
把下列各数分别填入相应的集合内:
0.101,
有理数集合
无理数集合
...
...
探究新知
负实数
正实数
数实
正有理数
负有理数
(2)按性质分
0
正无理数
负无理数
探究新知
无理数:
有理数:
负实数:
正实数:
例1 将下列各数分别填入下列相应的括号内:
对每个数都要进行判断,分类标准不同结果不同.
探究新知
你能分辩下列各数是哪个家庭的成员吗?
,
,
,
,
,
,
,
,
正数
负数
探究新知
思考1: 如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达A点,则数轴上表示点A的数是多少?
因为圆的周长为 π, 所以数轴上点A 表示的数是无理数 π.
0
-2
-1
1
3
2
4
●
●
●
●
●
●
●
●
●
●
●
●
●
●
A
巩固练习
思考2:你能在数轴上表示出 和 - 吗?
1
1
1
1
把两个边长为1的小正方形通过剪、拼,得到一个大正方形,大正方形的边长为 ,从而说明边长为1的小正方形的对角线为 .
巩固练习
-2
-1
0
1
2
-
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一点都表示一个实数.
★ 实数和数轴上的点是 一 一对应的.
巩固练习
例2:如图所示,数轴上A,B两点表示的数分别为-1和 ,点B关于点A的对称点为C,求点C所表示的实数.
解:∵数轴上A,B两点表示的数分别为-1和 ,
∴点B到点A的距离为1+ ,则点C到点A的距离为1+ ,
设点C表示的实数为x,则点A到点C的距离为-1-x,
∴-1-x=1+ ,
∴x=-2-
巩固练习
例3 如图所示,数轴上A,B两点表示的数分别为 和5.1,则A,B两点之间表示整数的点共有( )
A.6个 B.5个 C.4个 D.3个
C
巩固练习
解析:∵ ≈1.414,∴ 和5.1之间的整数有2,3,4,5, ∴A,B两点之间表示整数的点共有4个.
【方法总结】数轴上的点与实数一一对应,结合数轴分析,可轻松得出结论.
巩固练习
与有理数一样,实数也可以比较大小:
实数的大小比较
与有理数规定的大小一样,数轴上右边的点表示的实数比左边的点表示的实数大.
原点
0
正实数
负实数
<
巩固练习
1.正数大于零,负数小于零,正数大于负数;
2.两个正数,绝对值大的数较大;
3.两个负数,绝对值大的数反而小.
与有理数一样,在实数范围内:
巩固练习
,2可以分别看作是面积为5,4的正方形的边长,容易说明:面积较大的正方形,它的边长也较大,因此
同样,因为5<9,所以
不用计算器, 与2比较哪个大?与3比较呢?
巩固练习
例4 在数轴上表示下列各点,比较它们的大小,并用“<”连接它们.
-2 -1 0 1 2 3
1
-2
-2< < 1< <
例5 估计 位于( )
A.0~1之间 B.1~2之间 C.2~3之间 D.3~4之间
B
巩固练习
例6 比较下列各组数的大小:
解 : (1)因为 12 < 42,
所以 < 4,
所以 -1< 3;
(2)因为 10 > 32 ,
所以
所以
巩固练习
A. a 一定是正实数
B. 是有理数
C. 是有理数
D.数轴上任一点都对应一个有理数
B
1. 下列说法正确的是( )
巩固练习
2.有一个数值转换器,原理如下,当输x =81时,输出的y 是 ( )
A.9 B.3 C. D.±3
C
巩固练习
3. 判断快枪手 —— 看谁最快最准
(1)实数不是有理数就是无理数. ( )
(2)无理数都是无限不循环小数. ( )
(4)无理数都是无限小数. ( )
(3)带根号的数都是无理数. ( )
(5)无理数一定都带根号. ( )
×
×
巩固练习
4. 比较 与 6 的大小.
解: ∵37 >36
∴ > 6.
巩固练习
1.交换律 : 加法 a+b=b+a
乘法a×b=b×a
2.结合律: 加法(a+b)+c=a+(b+c)
乘法(a×b)×c=a×(b×c)
3.分配律: a× (b+c)= a×b+ a×c
注:有理数的运算律和运算法则在实数范围内同样适用
总结有理数的运算律和运算法则
巩固练习
实数的相反数、绝对值、倒数
相反数:
实数 a 的相反数是- a.若a与b互为相反数,则a+b=0.
绝对值:
实数a的绝对值,记为|a|,它是一个非负实数.
|a| =
a( a﹥0 )
0 ( a = 0)
-a( a﹤0)
几何意义: |a|表示点到原点0的距离.而| a-b |表示数a表示的点到数b表示的点的距离.
巩固练习
习题 6.3
巩固练习
巩固练习
巩固练习
巩固练习
巩固练习
巩固练习
巩固练习
巩固练习
1.无限不循环小数叫做无理数。
2.有理数和无理数统称实数。
3.实数按定义分类为有理数和无理数;按正负分类为正实数、0和负实数.
课堂小结
