人教版四年级数学下册表格式教案9 数学广角——鸡兔同笼
文档属性
| 名称 | 人教版四年级数学下册表格式教案9 数学广角——鸡兔同笼 | 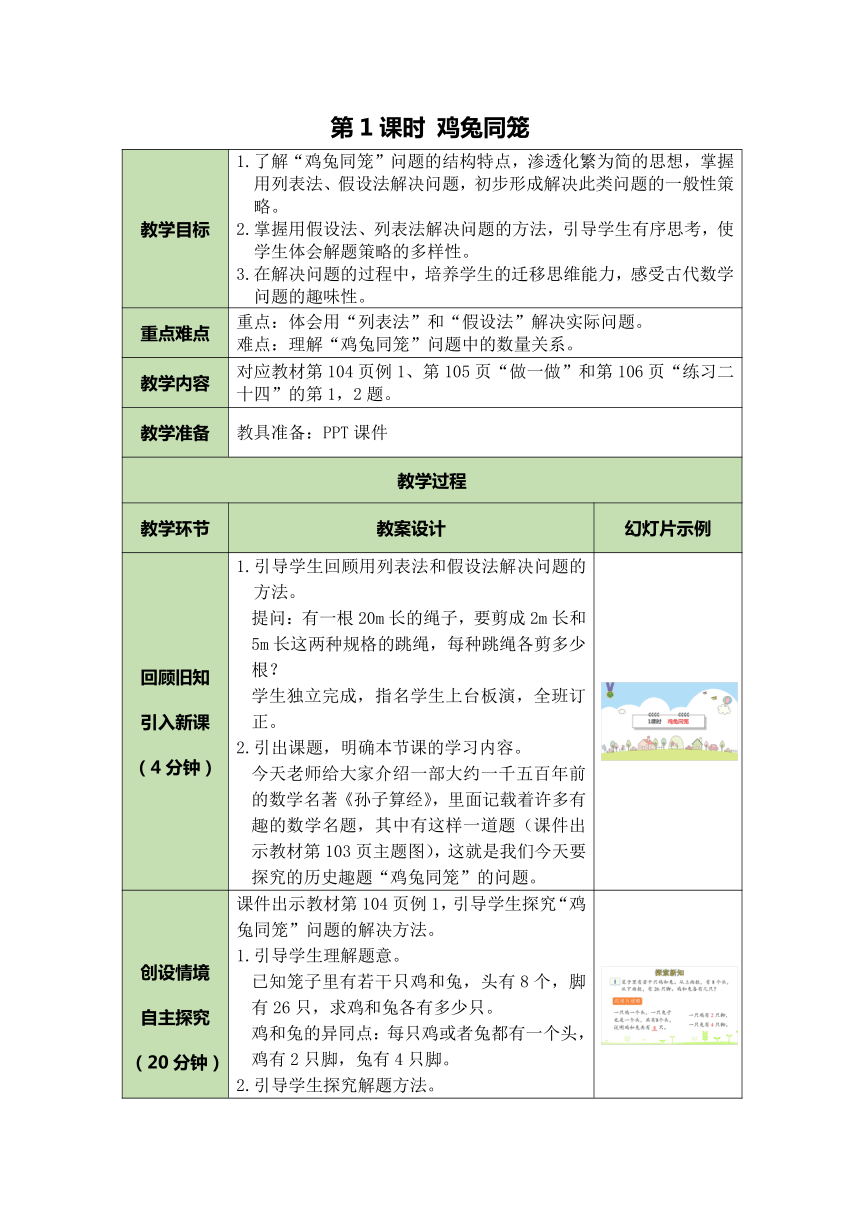 | |
| 格式 | zip | ||
| 文件大小 | 940.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-25 12:23:53 | ||
图片预览

文档简介
第1课时 鸡兔同笼
教学目标 1.了解“鸡兔同笼”问题的结构特点,渗透化繁为简的思想,掌握用列表法、假设法解决问题,初步形成解决此类问题的一般性策略。2.掌握用假设法、列表法解决问题的方法,引导学生有序思考,使学生体会解题策略的多样性。3.在解决问题的过程中,培养学生的迁移思维能力,感受古代数学问题的趣味性。
重点难点 重点:体会用“列表法”和“假设法”解决实际问题。难点:理解“鸡兔同笼”问题中的数量关系。
教学内容 对应教材第104页例1、第105页“做一做”和第106页“练习二十四”的第1,2题。
教学准备 教具准备:PPT课件
教学过程
教学环节 教案设计 幻灯片示例
回顾旧知引入新课(4分钟) 1.引导学生回顾用列表法和假设法解决问题的方法。提问:有一根20m长的绳子,要剪成2m长和5m长这两种规格的跳绳,每种跳绳各剪多少根?学生独立完成,指名学生上台板演,全班订正。2.引出课题,明确本节课的学习内容。今天老师给大家介绍一部大约一千五百年前的数学名著《孙子算经》,里面记载着许多有趣的数学名题,其中有这样一道题(课件出示教材第103页主题图),这就是我们今天要探究的历史趣题“鸡兔同笼”的问题。
创设情境自主探究(20分钟)创设情境自主探究(20分钟) 课件出示教材第104页例1,引导学生探究“鸡兔同笼”问题的解决方法。1.引导学生理解题意。已知笼子里有若干只鸡和兔,头有8个,脚有26只,求鸡和兔各有多少只。鸡和兔的异同点:每只鸡或者兔都有一个头,鸡有2只脚,兔有4只脚。2.引导学生探究解题方法。提问:鸡和兔各有几只?怎样计算?引导学生分组讨论算法,鼓励算法的多样化,汇报讨论结果:方法一:列表法。方法二:假设法。①假设全是鸡。如果笼子里全是鸡,那么就有8×2=16(只)脚,这样就少了26-16=10(只)脚。一只兔比一只鸡多2只脚,也就是有10÷2=5(只)兔。那么鸡就有8-5=3(只)。②假设全是兔。如果笼子里全是兔,那么就有8×4=32(只)脚,这样就多出了32-26=6(只)脚。一只鸡比一只兔少2只脚,也就是有6÷2=3(只)鸡。那么兔就有8-3=5(只)。3.引导学生进一步明确解题方法。提问:解决“鸡兔同笼”问题一般用哪些方法?哪一种最简便?需要注意什么问题?学生思考作答,教师强调:设鸡求兔,设兔求鸡,不要弄混。小结:解答“鸡兔同笼”问题可以用列表法、假设法等多种方法。当题中所给数据比较大,不宜采用列表法时,用假设法解决问题比较简便。
课堂练习巩固提高(12分钟) 1.完成教材第105页“做一做”。2.完成教材第106页“练习二十四”第1题。3.完成教材第106页“练习二十四”第2题。
课堂小结课后作业(4分钟) 1.(1)教师总结本节课的学习内容。(2)学生谈本节课学习的收获。2.布置作业。见本书配套练习题。
课堂板书
教学反思 “鸡兔同笼”对理解能力不够的学生来说有一定难度,特别是用假设法解答。因此,在教学过程中,不能提出统一要求,要允许不同的学生采用不同的解题方法。师生共同经历了列表法、假设法,最后比较哪种算法好,这样既培养了学生的探究能力和小组合作能力,又体现了算法的多样化。
教学目标 1.了解“鸡兔同笼”问题的结构特点,渗透化繁为简的思想,掌握用列表法、假设法解决问题,初步形成解决此类问题的一般性策略。2.掌握用假设法、列表法解决问题的方法,引导学生有序思考,使学生体会解题策略的多样性。3.在解决问题的过程中,培养学生的迁移思维能力,感受古代数学问题的趣味性。
重点难点 重点:体会用“列表法”和“假设法”解决实际问题。难点:理解“鸡兔同笼”问题中的数量关系。
教学内容 对应教材第104页例1、第105页“做一做”和第106页“练习二十四”的第1,2题。
教学准备 教具准备:PPT课件
教学过程
教学环节 教案设计 幻灯片示例
回顾旧知引入新课(4分钟) 1.引导学生回顾用列表法和假设法解决问题的方法。提问:有一根20m长的绳子,要剪成2m长和5m长这两种规格的跳绳,每种跳绳各剪多少根?学生独立完成,指名学生上台板演,全班订正。2.引出课题,明确本节课的学习内容。今天老师给大家介绍一部大约一千五百年前的数学名著《孙子算经》,里面记载着许多有趣的数学名题,其中有这样一道题(课件出示教材第103页主题图),这就是我们今天要探究的历史趣题“鸡兔同笼”的问题。
创设情境自主探究(20分钟)创设情境自主探究(20分钟) 课件出示教材第104页例1,引导学生探究“鸡兔同笼”问题的解决方法。1.引导学生理解题意。已知笼子里有若干只鸡和兔,头有8个,脚有26只,求鸡和兔各有多少只。鸡和兔的异同点:每只鸡或者兔都有一个头,鸡有2只脚,兔有4只脚。2.引导学生探究解题方法。提问:鸡和兔各有几只?怎样计算?引导学生分组讨论算法,鼓励算法的多样化,汇报讨论结果:方法一:列表法。方法二:假设法。①假设全是鸡。如果笼子里全是鸡,那么就有8×2=16(只)脚,这样就少了26-16=10(只)脚。一只兔比一只鸡多2只脚,也就是有10÷2=5(只)兔。那么鸡就有8-5=3(只)。②假设全是兔。如果笼子里全是兔,那么就有8×4=32(只)脚,这样就多出了32-26=6(只)脚。一只鸡比一只兔少2只脚,也就是有6÷2=3(只)鸡。那么兔就有8-3=5(只)。3.引导学生进一步明确解题方法。提问:解决“鸡兔同笼”问题一般用哪些方法?哪一种最简便?需要注意什么问题?学生思考作答,教师强调:设鸡求兔,设兔求鸡,不要弄混。小结:解答“鸡兔同笼”问题可以用列表法、假设法等多种方法。当题中所给数据比较大,不宜采用列表法时,用假设法解决问题比较简便。
课堂练习巩固提高(12分钟) 1.完成教材第105页“做一做”。2.完成教材第106页“练习二十四”第1题。3.完成教材第106页“练习二十四”第2题。
课堂小结课后作业(4分钟) 1.(1)教师总结本节课的学习内容。(2)学生谈本节课学习的收获。2.布置作业。见本书配套练习题。
课堂板书
教学反思 “鸡兔同笼”对理解能力不够的学生来说有一定难度,特别是用假设法解答。因此,在教学过程中,不能提出统一要求,要允许不同的学生采用不同的解题方法。师生共同经历了列表法、假设法,最后比较哪种算法好,这样既培养了学生的探究能力和小组合作能力,又体现了算法的多样化。
