人教版八年级数学下册课件 16.3.2二次根式的混合运算(共33张ppt)
文档属性
| 名称 | 人教版八年级数学下册课件 16.3.2二次根式的混合运算(共33张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-26 11:44:24 | ||
图片预览









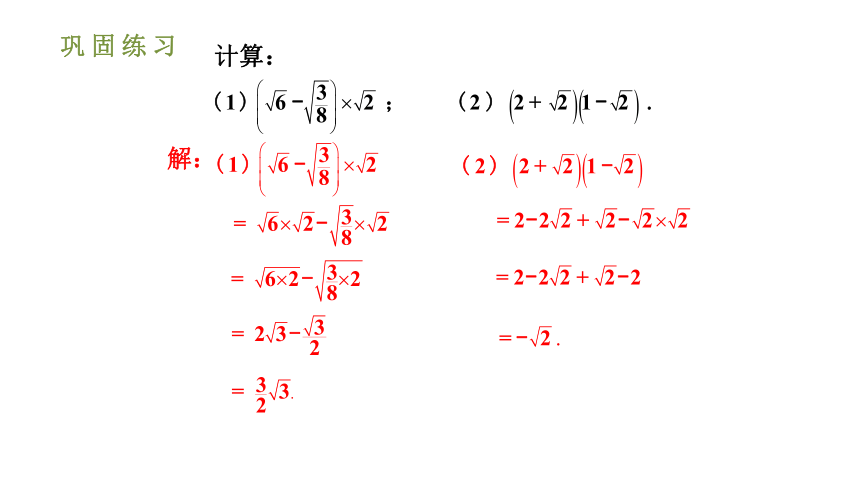


文档简介
(共33张PPT)
16 二次根式
16.3 二次根式的加减
第二课时 二次根式的混合运算
课时目标
1. 掌握二次根式的混合运算的运算法则。
2.会运用二次根式的混合运算法则进行有关的运算。
情景导入
问题1 单项式与多项式、多项式与多项式的乘法法则法则分别是什么?
问题2 多项式与单项式的除法法则是什么?
m(a+b+c)=ma+mb+mc;
(m+n)(a+b)=ma+mb+na+nb
(ma+mb+mc)÷m=a+b+c
探究新知
单×多
分配律
转化
前面两个问题的思路是:
思考 若把字母a,b,c,m都用二次根式代替(每个同学任选一组),然后对比归纳,你们发现了什么?
单×单
探究新知
二次根式的混合运算及应用
二次根式的加、减、乘、除混合运算与整式运算一样,体现在:运算律、运算顺序、乘法法则仍然适用.
例1 计算:
解:
探究新知
解:
此处类比“多项式×多项式”即(x+a)(x+b)=x2+(a+b)x+ab.
二次根式的混合运算,先要弄清运算种类,再确定运算顺序:先乘除,再加减,有括号的要算括号内的,最后按照二次根式的相应的运算法则进行.
探究新知
解:(1)原式
(2)原式
【变式题】计算:
有绝对值符号的,同括号一样,先去绝对值,注意去掉绝对值后,得到的数应该为正数.
探究新知
例2 甲、乙两个城市间计划修建一条城际铁路, 其中有一段路基的横断面设计为上底宽 ,下底宽 ,高 的梯形,这段路基长 500 m,那么这段路基的土石方 (即路基的体积,其中路基的体积=路基横断面面积×路基的长度)为多少立方米呢?
探究新知
解:路基的土石方等于路基横断面面积乘以路基的长度,所以这段路基的土石方为:
答:这段路基的土石方为
巩固练习
计算:
解:
探究新知
利用乘法公式进行二次根式的运算
问题1 整式乘法运算中的乘法公式有哪些?
平方差公式:(a+b)(a-b)=a2-b2;
完全平方公式:(a+b)2=a2+2ab+b2;
(a-b)2=a2-2ab+b2.
问题2 整式的乘法公式对于二次根式的运算也适用吗?
整式的乘法公式就是多项式×多项式
前面我们已经知道二次根式运算类比整式运算.
探究新知
例3 计算:
解:
探究新知
解:
探究新知
进行二次根式的混合运算时,一般先将二次根式转化为最简二次根式,再根据题目的特点确定合适的运算方法,同时要灵活运用乘法公式,因式分解等来简化运算.
探究新知
【变式题】计算:
解:(1)原式
(2)原式
巩固练习
计算:
探究新知
例3 已知 试求x2+2xy+y2的值.
解:x2+2xy+y2=(x+y)2
把 代入上式得
原式=
求代数式的值
探究新知
解:∵ ,
∴
∴ x3y+xy3=xy(x2+y2)=xy[(x+y)2-2xy]
【变式题】 已知 ,求x3y+xy3.
探究新知
用整体代入法求代数式值的方法:求关于x,y的对称式(即交换任意两个字母的位置后,代数式不变)的值,一般先求x+y,xy,x-y , 等的值,然后将所求代数式适当变形成知含x+y,xy,x-y , 等式子,再代入求值.
探究新知
在前面我们学习了二次根式的除法法则时,学会了怎样去掉分母的二次根式的方法,比如:
思考 如果分母不是单个的二次根式,而是含二次根式的式子,如: 等,该怎样去掉分母中的二次根式呢?
拓展探究
探究新知
例4 计算:
解:
探究新知
分母形如 的式子,分子、分母同乘以
的式子,构成平方差公式,可以使分母不含根号.
探究新知
【变式题】 已知 ,求 .
解:∵
解决二次根式的化简求值问题时,先化简已知条件,再用乘法公式变形、代入求值即可.
巩固练习
已知 的整数部分是a,小数部分是b,求a2-b2的值.
解:
巩固练习
1.下列计算中正确的是( )
B
2.计算:
5
3.设 则a b(填“>”“<”或“=”).
=
巩固练习
4.计算:
解:
巩固练习
解:原式
巩固练习
5.在一个边长为 cm的正方形内部,挖去一个边长为 cm的正方形,求剩余部分的面积.
解:由题意得
即剩余部分的面积是
6.(1) 已知 ,求 的值;
巩固练习
解:x2-2x-3=(x-3)(x+1)
(2)已知 ,求 的值.
解:
巩固练习
6.阅读下列材料,然后回答问题:
在进行类似于二次根式 的运算时,通常有如下两种方法将其进一步化简:
方法一:
方法二:
巩固练习
(1)请用两种不同的方法化简:
(2)化简:
解:(1)?
?
巩固练习
课堂小结
二次根式混合运算
乘法公式
化简求值
分母有理化
化简已知条件和所求代数式
(a+b)(a-b)=a2-b2
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
(x+a)(x+b)=x2+(a+b)x+ab
16 二次根式
16.3 二次根式的加减
第二课时 二次根式的混合运算
课时目标
1. 掌握二次根式的混合运算的运算法则。
2.会运用二次根式的混合运算法则进行有关的运算。
情景导入
问题1 单项式与多项式、多项式与多项式的乘法法则法则分别是什么?
问题2 多项式与单项式的除法法则是什么?
m(a+b+c)=ma+mb+mc;
(m+n)(a+b)=ma+mb+na+nb
(ma+mb+mc)÷m=a+b+c
探究新知
单×多
分配律
转化
前面两个问题的思路是:
思考 若把字母a,b,c,m都用二次根式代替(每个同学任选一组),然后对比归纳,你们发现了什么?
单×单
探究新知
二次根式的混合运算及应用
二次根式的加、减、乘、除混合运算与整式运算一样,体现在:运算律、运算顺序、乘法法则仍然适用.
例1 计算:
解:
探究新知
解:
此处类比“多项式×多项式”即(x+a)(x+b)=x2+(a+b)x+ab.
二次根式的混合运算,先要弄清运算种类,再确定运算顺序:先乘除,再加减,有括号的要算括号内的,最后按照二次根式的相应的运算法则进行.
探究新知
解:(1)原式
(2)原式
【变式题】计算:
有绝对值符号的,同括号一样,先去绝对值,注意去掉绝对值后,得到的数应该为正数.
探究新知
例2 甲、乙两个城市间计划修建一条城际铁路, 其中有一段路基的横断面设计为上底宽 ,下底宽 ,高 的梯形,这段路基长 500 m,那么这段路基的土石方 (即路基的体积,其中路基的体积=路基横断面面积×路基的长度)为多少立方米呢?
探究新知
解:路基的土石方等于路基横断面面积乘以路基的长度,所以这段路基的土石方为:
答:这段路基的土石方为
巩固练习
计算:
解:
探究新知
利用乘法公式进行二次根式的运算
问题1 整式乘法运算中的乘法公式有哪些?
平方差公式:(a+b)(a-b)=a2-b2;
完全平方公式:(a+b)2=a2+2ab+b2;
(a-b)2=a2-2ab+b2.
问题2 整式的乘法公式对于二次根式的运算也适用吗?
整式的乘法公式就是多项式×多项式
前面我们已经知道二次根式运算类比整式运算.
探究新知
例3 计算:
解:
探究新知
解:
探究新知
进行二次根式的混合运算时,一般先将二次根式转化为最简二次根式,再根据题目的特点确定合适的运算方法,同时要灵活运用乘法公式,因式分解等来简化运算.
探究新知
【变式题】计算:
解:(1)原式
(2)原式
巩固练习
计算:
探究新知
例3 已知 试求x2+2xy+y2的值.
解:x2+2xy+y2=(x+y)2
把 代入上式得
原式=
求代数式的值
探究新知
解:∵ ,
∴
∴ x3y+xy3=xy(x2+y2)=xy[(x+y)2-2xy]
【变式题】 已知 ,求x3y+xy3.
探究新知
用整体代入法求代数式值的方法:求关于x,y的对称式(即交换任意两个字母的位置后,代数式不变)的值,一般先求x+y,xy,x-y , 等的值,然后将所求代数式适当变形成知含x+y,xy,x-y , 等式子,再代入求值.
探究新知
在前面我们学习了二次根式的除法法则时,学会了怎样去掉分母的二次根式的方法,比如:
思考 如果分母不是单个的二次根式,而是含二次根式的式子,如: 等,该怎样去掉分母中的二次根式呢?
拓展探究
探究新知
例4 计算:
解:
探究新知
分母形如 的式子,分子、分母同乘以
的式子,构成平方差公式,可以使分母不含根号.
探究新知
【变式题】 已知 ,求 .
解:∵
解决二次根式的化简求值问题时,先化简已知条件,再用乘法公式变形、代入求值即可.
巩固练习
已知 的整数部分是a,小数部分是b,求a2-b2的值.
解:
巩固练习
1.下列计算中正确的是( )
B
2.计算:
5
3.设 则a b(填“>”“<”或“=”).
=
巩固练习
4.计算:
解:
巩固练习
解:原式
巩固练习
5.在一个边长为 cm的正方形内部,挖去一个边长为 cm的正方形,求剩余部分的面积.
解:由题意得
即剩余部分的面积是
6.(1) 已知 ,求 的值;
巩固练习
解:x2-2x-3=(x-3)(x+1)
(2)已知 ,求 的值.
解:
巩固练习
6.阅读下列材料,然后回答问题:
在进行类似于二次根式 的运算时,通常有如下两种方法将其进一步化简:
方法一:
方法二:
巩固练习
(1)请用两种不同的方法化简:
(2)化简:
解:(1)?
?
巩固练习
课堂小结
二次根式混合运算
乘法公式
化简求值
分母有理化
化简已知条件和所求代数式
(a+b)(a-b)=a2-b2
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
(x+a)(x+b)=x2+(a+b)x+ab
