湘教版七年级数学下册课件:1.1建立二元一次方程组(共26张PPT)
文档属性
| 名称 | 湘教版七年级数学下册课件:1.1建立二元一次方程组(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-26 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
1.1
建立二元一次方程组
湘教版
七年级下册
学习目标
1.了解二元一次方程(组)及其解的定义.
2.会检验一对数值是不是某个二元一次方程组的解.(重点)
3.能根据实际问题列出简单的二元一次方程组.(难点)
我们家1月份的天然气费和水费共60元,其中天然气费比水费多20元.你知道天然气费和水费各是多少吗?
动脑筋
可以设1月份的天然气费是x元,则水费是______元,由题意列出一元一次方程:_____________.
既要求水费,又要求天然气费……
新课导入
想一想,还有其他方法吗?
可以设1月份的天然气费是x元,水费是y元,由题意得
观察方程①和②各含有几个未知数?
含未知数的项的次数是多少?
含有两个未知数(二元),并且未知项的次数都是1的方程叫二元一次方程.
①
②
(8)4xy+5=0
(1)x+y=11
(3)x2+y=5
(2)m+1=2
(4)3x-π=11
(5)
-5x=4y+2
(6)7+a=2b+11c
(7)7x+
=13
y
2
二元一次方程
不是二元一次方程
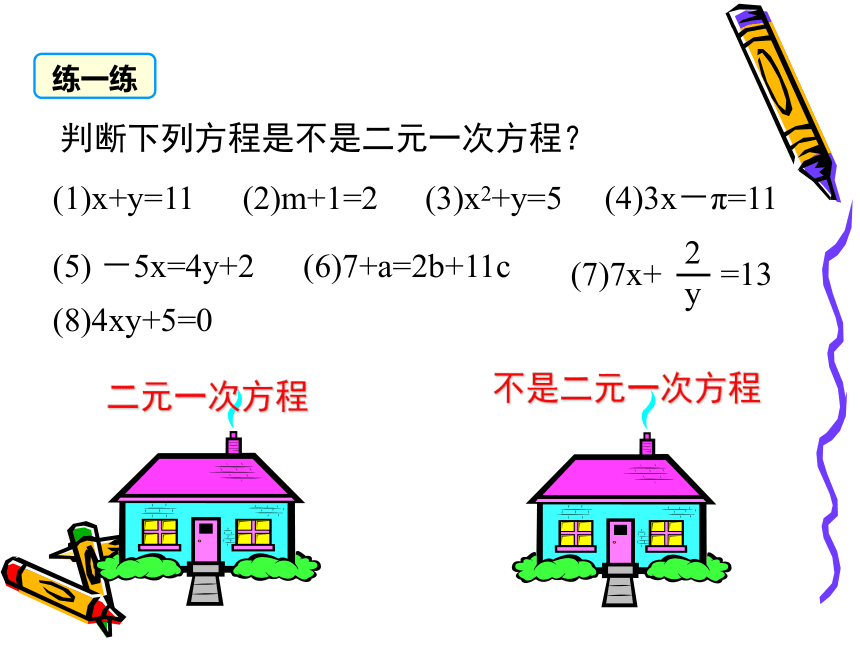
判断下列方程是不是二元一次方程?
练一练
例
已知|m-1|x|m|+y2n-1=3是二元一次方程,
则m+n=________.
典例精析
解析:根据题意得|m|=1且|m-1|≠0,2n-1=1,解得m=-1,n=1,所以m+n=0.
0
由方程是二元一次方程可知:
(1)未知数的系数不为0;
(2)未知数的次数都是1.
方法
练一练
若x2m-1+5y3n-2m
=7是二元一次方程,则m=____,n=____.
2m-1=1
1
3n-2m=1
1
方程①和②中,
x都表示1月份的天然气费,y都表示1月份的水费,它们必须同时满足方程①和②,因此把方程①和②用大括号联立起来,得
①
②
像这样把两个含有相同未知数的二元一次方程(或者一个二元一次方
程,一个一元一次方程)联立起来,组成的方程组,叫做二元一次方程组.
含有两个未知数的几个一次方程所组成的方程组,叫二元一次方程组.
推进新课
紧扣相关概念
下列方程组是二元一次方程组的是(
)
A.
B.
C.
D.
B
练一练
小提示:
也是二元一次方程组.
把x=40,y=20代入方程组
的每一个方程中,每一个方程左、右两边的值相等吗?
40+20=60,40-20=20
.
每一个方程左、右两边的值都相等.
在一个二元一次方程组中,使每一个方程的左右两边的值都相等的一组未知数的值,叫做这个方程组的一个解.
我们把x=40,y=20叫做二元一次方程组
的一个解.这个解通常记做
求方程组的解的过程叫做解方程组.
例
小玲在文具店买了3本练习本,2支圆珠笔,共花去8元,其中购买的练习本比圆珠笔多花4元.
(1)为了知道练习本、圆珠笔的单价是多少元,你能列出相应的方程组吗?
(2)
是列出的二元一次方程组的解吗?
解(1)
设练习本的单价是x元,
圆珠笔的单价是y元.
根据题意得
(2)
把
代入方程②中,左边=右边,
所以
是方程组
的解.
3本练习本,2支圆珠笔共花8元.
3x
2y
+
=
8
购买的练习本比圆珠笔多花4元.
3x
2y
-
=
4
1.
是上例中方程组的解吗?
解
把
代入方程①中,左边≠右边,
把
代入方程②中,左边≠右边,
所以
不是方程组
的解.
2.
一条船顺流航行,每小时行24
km;逆流航行,
每小时行18
km.
(1)为了求轮船在静水中的速度x与水的流速y,你能
列出相应的方程组吗?
解
设轮船在静水中的速度为x,水的流速为y.
根据题意得
(2)
是列出的二元一次方程组的解吗?
解
把
代入方程①中,左边=右边,
把
代入方程②中,左边=右边,
所以
是方程组
的解.
3.
是下列哪个方程组的解?
解
(1)把
代入第一个方程中,左边=右边,
把
代入第二个方程中,左边=右边,
所以
是方程组
的解.
解(2)把
代入第一个方程中,左边=右边,
把
代入第二个方程中,左边≠右边,
所以
不是方程组
的解.
1.
二元一次方程组
的解是(
).
C
通过计算得
x=1,y=1或“特殊值法”,将A、B、C、D逐一代入方程组检验,只有C项正确,故选C.
解析
2.若关于x,y的二元一次方程组
的解也是二元一次方程2x+3y=6的解,则k的值为(
).
B
解析
由
解得
代入2x+3y=6,
得
,故选B.
4.二元一次方程组
的解是(
)
A.
B.
C.
D.
C
x+
=1,
y+x=2
3.下列不是二元一次方程组的是(
)
A.
x+y=3,
x-y=1
B.
C.
D.
6x+4y=9,
y=3x+4
B
x=1,
y=1
x=1,
y=3
2x+y=5,
3x-2y=4
x=1,
y=2
x=2,
y=1
x=2,
y=-1
5.关于x、y的方程ax2+bx+2y=3是一个二元一次方程,则a、b的值分别为(
)
A
.a=0且
b=0
B.a=0或
b=0
C.
a=0且
b≠0
D.a≠0且
b≠0
C
6.已知
是方程2x-4y+2a=3一组解,则a=____.
7.若方程2x2m+3+3y3n-7=0
是关于x、y的二元一次方程,则m=______,n=______;
x=3,
y=1
1
2
-1
8
3
8.写出方程x+2y=5
在自然数范围内的所有解.
x=1,
y=2
x=3,
y=1
x=5,
y=0
拓展提升
学有所思,感悟收获
谈谈你的收获
能说出你这节课的收获和体验
让大家与你分享吗?
谢谢,请提出宝贵意见!
1.1
建立二元一次方程组
湘教版
七年级下册
学习目标
1.了解二元一次方程(组)及其解的定义.
2.会检验一对数值是不是某个二元一次方程组的解.(重点)
3.能根据实际问题列出简单的二元一次方程组.(难点)
我们家1月份的天然气费和水费共60元,其中天然气费比水费多20元.你知道天然气费和水费各是多少吗?
动脑筋
可以设1月份的天然气费是x元,则水费是______元,由题意列出一元一次方程:_____________.
既要求水费,又要求天然气费……
新课导入
想一想,还有其他方法吗?
可以设1月份的天然气费是x元,水费是y元,由题意得
观察方程①和②各含有几个未知数?
含未知数的项的次数是多少?
含有两个未知数(二元),并且未知项的次数都是1的方程叫二元一次方程.
①
②
(8)4xy+5=0
(1)x+y=11
(3)x2+y=5
(2)m+1=2
(4)3x-π=11
(5)
-5x=4y+2
(6)7+a=2b+11c
(7)7x+
=13
y
2
二元一次方程
不是二元一次方程
判断下列方程是不是二元一次方程?
练一练
例
已知|m-1|x|m|+y2n-1=3是二元一次方程,
则m+n=________.
典例精析
解析:根据题意得|m|=1且|m-1|≠0,2n-1=1,解得m=-1,n=1,所以m+n=0.
0
由方程是二元一次方程可知:
(1)未知数的系数不为0;
(2)未知数的次数都是1.
方法
练一练
若x2m-1+5y3n-2m
=7是二元一次方程,则m=____,n=____.
2m-1=1
1
3n-2m=1
1
方程①和②中,
x都表示1月份的天然气费,y都表示1月份的水费,它们必须同时满足方程①和②,因此把方程①和②用大括号联立起来,得
①
②
像这样把两个含有相同未知数的二元一次方程(或者一个二元一次方
程,一个一元一次方程)联立起来,组成的方程组,叫做二元一次方程组.
含有两个未知数的几个一次方程所组成的方程组,叫二元一次方程组.
推进新课
紧扣相关概念
下列方程组是二元一次方程组的是(
)
A.
B.
C.
D.
B
练一练
小提示:
也是二元一次方程组.
把x=40,y=20代入方程组
的每一个方程中,每一个方程左、右两边的值相等吗?
40+20=60,40-20=20
.
每一个方程左、右两边的值都相等.
在一个二元一次方程组中,使每一个方程的左右两边的值都相等的一组未知数的值,叫做这个方程组的一个解.
我们把x=40,y=20叫做二元一次方程组
的一个解.这个解通常记做
求方程组的解的过程叫做解方程组.
例
小玲在文具店买了3本练习本,2支圆珠笔,共花去8元,其中购买的练习本比圆珠笔多花4元.
(1)为了知道练习本、圆珠笔的单价是多少元,你能列出相应的方程组吗?
(2)
是列出的二元一次方程组的解吗?
解(1)
设练习本的单价是x元,
圆珠笔的单价是y元.
根据题意得
(2)
把
代入方程②中,左边=右边,
所以
是方程组
的解.
3本练习本,2支圆珠笔共花8元.
3x
2y
+
=
8
购买的练习本比圆珠笔多花4元.
3x
2y
-
=
4
1.
是上例中方程组的解吗?
解
把
代入方程①中,左边≠右边,
把
代入方程②中,左边≠右边,
所以
不是方程组
的解.
2.
一条船顺流航行,每小时行24
km;逆流航行,
每小时行18
km.
(1)为了求轮船在静水中的速度x与水的流速y,你能
列出相应的方程组吗?
解
设轮船在静水中的速度为x,水的流速为y.
根据题意得
(2)
是列出的二元一次方程组的解吗?
解
把
代入方程①中,左边=右边,
把
代入方程②中,左边=右边,
所以
是方程组
的解.
3.
是下列哪个方程组的解?
解
(1)把
代入第一个方程中,左边=右边,
把
代入第二个方程中,左边=右边,
所以
是方程组
的解.
解(2)把
代入第一个方程中,左边=右边,
把
代入第二个方程中,左边≠右边,
所以
不是方程组
的解.
1.
二元一次方程组
的解是(
).
C
通过计算得
x=1,y=1或“特殊值法”,将A、B、C、D逐一代入方程组检验,只有C项正确,故选C.
解析
2.若关于x,y的二元一次方程组
的解也是二元一次方程2x+3y=6的解,则k的值为(
).
B
解析
由
解得
代入2x+3y=6,
得
,故选B.
4.二元一次方程组
的解是(
)
A.
B.
C.
D.
C
x+
=1,
y+x=2
3.下列不是二元一次方程组的是(
)
A.
x+y=3,
x-y=1
B.
C.
D.
6x+4y=9,
y=3x+4
B
x=1,
y=1
x=1,
y=3
2x+y=5,
3x-2y=4
x=1,
y=2
x=2,
y=1
x=2,
y=-1
5.关于x、y的方程ax2+bx+2y=3是一个二元一次方程,则a、b的值分别为(
)
A
.a=0且
b=0
B.a=0或
b=0
C.
a=0且
b≠0
D.a≠0且
b≠0
C
6.已知
是方程2x-4y+2a=3一组解,则a=____.
7.若方程2x2m+3+3y3n-7=0
是关于x、y的二元一次方程,则m=______,n=______;
x=3,
y=1
1
2
-1
8
3
8.写出方程x+2y=5
在自然数范围内的所有解.
x=1,
y=2
x=3,
y=1
x=5,
y=0
拓展提升
学有所思,感悟收获
谈谈你的收获
能说出你这节课的收获和体验
让大家与你分享吗?
谢谢,请提出宝贵意见!
