人教版七年级数学下册课件:8.3实际问题(路程问题)与二元一次方程组(共27张PPT)
文档属性
| 名称 | 人教版七年级数学下册课件:8.3实际问题(路程问题)与二元一次方程组(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-26 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
人教版
七年级数学下册
8.3实际问题与二元一次方程组
行
程
问
题
第八章
二元一次方程组
目标导航
1.能够根据具体的数量关系,列出二元一次方程组解决简单的实际问题.(重点)
2.学会利用二元一次方程组解决几何、行程问题.(重点、难点)
行程问题中关系式
路程=时间×速度
时间=路程÷速度
速度=路程÷时间
复习回顾
悟空顺风探妖踪,
千里只行四分钟.
归时四分行六百,
风速多少才称雄?
顺风速度=悟空行走速度+风速
逆风速度=悟空行走速度-风速
例方程组解决行程问题
问题再现,探究新法
解:设悟空行走速度是每分钟x里,
风速是每分钟y里,则
4(x-y)=600
x=200
y=50
答:风速是每分钟50里。
4(x+y)=1000
解得:
依题意得
立方程组解决行程问题
顺风速度=悟空行走速度+风速
逆风速度=悟空行走速度-风速
悟空顺风探妖踪,
千里只行四分钟.
归时四分行六百,
风速多少才称雄?
1.一船顺水航行45千米需要3小时,逆水航行65千米需要5小时,若设船在静水中的速度为x千米/小时,水流的速度为y㎞/h,则x、y的值为
(
)
A、X=3,y=2
B、x=14,y=1
C、x=15,y=1
E、x=14,y=2
B
练习
小试牛刀
2、我国的长江由西至东奔腾不息,其中九江至南京约有450千米的路程,某船从九江出发9个小时就能到达南京;返回时则用多了1个小时.求此船在静水中的速度以及长江水的平均流速.
解:设轮船在静水中的速度为x千米/时,长江水的平均流速为y千米/时.
答:轮船在静水中的速度为47.5千米/时,长江水的平均流速为2.5千米/时.
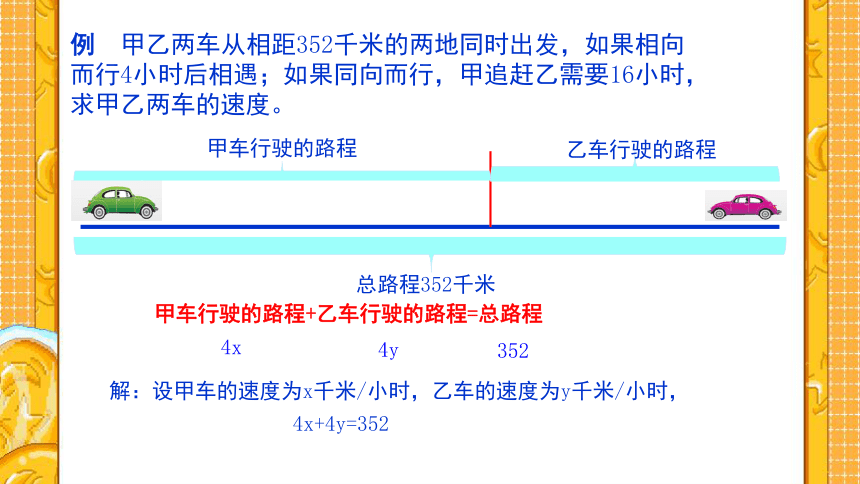
例
甲乙两车从相距352千米的两地同时出发,如果相向
而行4小时后相遇;如果同向而行,甲追赶乙需要16小时,
求甲乙两车的速度。
总路程352千米
甲车行驶的路程
乙车行驶的路程
甲车行驶的路程+乙车行驶的路程=总路程
解:设甲车的速度为x千米/小时,乙车的速度为y千米/小时,
4x
4y
352
4x+4y=352
例
甲乙两人开车从相距352千米的两地同时出发,如果相向而行4小时后相遇;如果同向而行,甲追赶乙需要16小时,求甲乙两车的速度。
352千米
甲行驶的路程
乙行驶的路程
解:设甲车的速度为x千米/小时,乙车的速度为y千米/小时,
甲车行驶的路程
-乙车行驶的路程=原来相距的路程
4x+4y=352
16x
16y
352
16x-16y=352
x=55
y=33
答:甲车的速度为55千米/小时,乙车的速度为33千米/小时。
解得
变式训练
张强与李毅二人分别从相距
20
千米的两地出发,相向而行。如果张强比李毅早出发
30
分钟,那么在李毅出发后
2
小时,他们相遇;如果他们同时出发,那么
1
小时后两人还相距
11
千米。求张强、李毅每小时各走多少千米?
2y千米
张强2.5小时走的路程
李毅2小时走的路程
11千米
0.5x千米
2x千米
(1)
A
B
x千米
y千米
(2)
A
B
变式训练
张强与李毅二人分别从相距
20
千米的两地出发,相向而行。如果张强比李毅早出发
30
分钟,那么在李毅出发后
2
小时,他们相遇;如果他们同时出发,那么
1
小时后两人还相距
11
千米。求张强、李毅每小时各走多少千米?
设张强每小时走
x
千米
李毅每小时走
y
千米
1.某车站有甲、乙两辆汽车,若甲车先出发1h后乙车出发,则乙车出发后5h追上甲车;若甲车先开出20km后乙车出发,则乙车出发4h后追上甲车,求甲乙两车的速度。
巩固训练
2.甲、乙两人在周长为400m的环形跑道上练跑,如果相向出发,每隔2.5min相遇一次;如果同向出发,每隔10min相遇一次,假定两人速度不变,且甲快乙慢,求甲、乙两人的速度.
3、小李骑自行车从A地到B地,小明骑自行车从B地到A地,两人都匀速前进,已知两人在上午8时同时出发,到上午10时,两人还相距36千米,到中午12时,两人又相距36千米,求A,B两地间的路程.
总结
2.追及问题
1.相遇问题
甲的路程+乙的路程=总的路程
快者的路程-慢者的路程=原来相距路程
二.做题技巧
画线段图找等量关系
一.行程问题等量关系
合作探究---列方程组解决行程问题问题
从甲地到乙地有一段上坡与一段平路。如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需54min,从乙地到甲地需42min,甲地到乙地全程是多少?
合作探究---列方程组解决行程问题问题
分析:甲地到乙地的路分成两段,一段为平路,一段为下坡路.
平路:4
m/h
下坡路:5
m/h
上坡路:3
m/h
走平路的时间+走下坡路的时间=________,
走上坡路的时间+走平路的时间=
_______.
42min
54min
合作探究---列方程组解决行程问题问题
平路时间
坡路时间
总时间
甲到乙
乙到甲
解:设甲地到乙地平路长x
m,上坡路长y
m.
根据题意,可列方程组:
解方程组,得
答:甲地到乙地的距离是3.1千米。
所以1.6+1.5=3.1(km)
本题还有其他方法吗?
小试牛刀
1、甲、乙两人相距4km,以各自的速度同时出发.如果同向而行,甲2h追上乙;如果相向而行,两人0.5h后相遇.试问两人的速度各是多少?
分析:对于行程问题,一般可以借助示意图表示题中的数量关系,可以更加直观的找到相等关系.
小试牛刀
(1)
同时出发,同向而行
甲出发点
乙出发点
4km
甲追上乙
乙2h行程
甲2h行程
甲2h行程=4km+乙2h行程
(2)
同时出发,相向而行
甲出发点
乙出发点
4km
相遇地
甲0.5h
行程
乙0.5h
行程
甲0.5h行程+乙0.5h行程=4km
小试牛刀
解:设甲、乙的速度分别为xkm/h,ykm/h.
根据题意,得
解方程组,得
答:甲的速度为5km/h,乙的速度为3km/h.
1.一船顺水航行45千米需要3小时,逆水航行65千米需要5小时,若设船在静水中的速度为x千米/小时,水流的速度为y㎞/h,则x、y的值为
(
)
A、X=3,y=2
B、x=14,y=1
C、x=15,y=1
E、x=14,y=2
B
当堂达标
2.甲、乙二人相距6km,二人同时出发。同向而行,甲3小时可追上乙;相向而行,1小时相遇。二人的平均速度各是多少?
6km
(1)甲3小时行驶路程=乙3小时行驶+6
(2)甲3小时行驶+乙3小时行驶=6
当堂达标
实际问题
数学问题
(二元一次方程组)
解方程组
数学问题的解
(二元一次方程组的解)
双检验
实际问题
的答案
代入法
加减法
(消元)
设未知数、列方程组
利用二元一次方程组分析和解决实际问题的基本过程:
方法归纳
请你说给大家听听
这节课你有哪些收获?
体会.分享
二元一次方程组的应用
应用
步骤
简单实际问题
行程问题
路程=平均速度×时间
审题:弄清题意和题目中的
设元:用_____表示题目中的未知数
列方程组:根据__个等量关系列出方程组
解方程组
检验作答
数量关系
字母
2
代入法;
加减法.
几何问题
?
课堂
小结
谢谢同学们的努力!
人教版
七年级数学下册
8.3实际问题与二元一次方程组
行
程
问
题
第八章
二元一次方程组
目标导航
1.能够根据具体的数量关系,列出二元一次方程组解决简单的实际问题.(重点)
2.学会利用二元一次方程组解决几何、行程问题.(重点、难点)
行程问题中关系式
路程=时间×速度
时间=路程÷速度
速度=路程÷时间
复习回顾
悟空顺风探妖踪,
千里只行四分钟.
归时四分行六百,
风速多少才称雄?
顺风速度=悟空行走速度+风速
逆风速度=悟空行走速度-风速
例方程组解决行程问题
问题再现,探究新法
解:设悟空行走速度是每分钟x里,
风速是每分钟y里,则
4(x-y)=600
x=200
y=50
答:风速是每分钟50里。
4(x+y)=1000
解得:
依题意得
立方程组解决行程问题
顺风速度=悟空行走速度+风速
逆风速度=悟空行走速度-风速
悟空顺风探妖踪,
千里只行四分钟.
归时四分行六百,
风速多少才称雄?
1.一船顺水航行45千米需要3小时,逆水航行65千米需要5小时,若设船在静水中的速度为x千米/小时,水流的速度为y㎞/h,则x、y的值为
(
)
A、X=3,y=2
B、x=14,y=1
C、x=15,y=1
E、x=14,y=2
B
练习
小试牛刀
2、我国的长江由西至东奔腾不息,其中九江至南京约有450千米的路程,某船从九江出发9个小时就能到达南京;返回时则用多了1个小时.求此船在静水中的速度以及长江水的平均流速.
解:设轮船在静水中的速度为x千米/时,长江水的平均流速为y千米/时.
答:轮船在静水中的速度为47.5千米/时,长江水的平均流速为2.5千米/时.
例
甲乙两车从相距352千米的两地同时出发,如果相向
而行4小时后相遇;如果同向而行,甲追赶乙需要16小时,
求甲乙两车的速度。
总路程352千米
甲车行驶的路程
乙车行驶的路程
甲车行驶的路程+乙车行驶的路程=总路程
解:设甲车的速度为x千米/小时,乙车的速度为y千米/小时,
4x
4y
352
4x+4y=352
例
甲乙两人开车从相距352千米的两地同时出发,如果相向而行4小时后相遇;如果同向而行,甲追赶乙需要16小时,求甲乙两车的速度。
352千米
甲行驶的路程
乙行驶的路程
解:设甲车的速度为x千米/小时,乙车的速度为y千米/小时,
甲车行驶的路程
-乙车行驶的路程=原来相距的路程
4x+4y=352
16x
16y
352
16x-16y=352
x=55
y=33
答:甲车的速度为55千米/小时,乙车的速度为33千米/小时。
解得
变式训练
张强与李毅二人分别从相距
20
千米的两地出发,相向而行。如果张强比李毅早出发
30
分钟,那么在李毅出发后
2
小时,他们相遇;如果他们同时出发,那么
1
小时后两人还相距
11
千米。求张强、李毅每小时各走多少千米?
2y千米
张强2.5小时走的路程
李毅2小时走的路程
11千米
0.5x千米
2x千米
(1)
A
B
x千米
y千米
(2)
A
B
变式训练
张强与李毅二人分别从相距
20
千米的两地出发,相向而行。如果张强比李毅早出发
30
分钟,那么在李毅出发后
2
小时,他们相遇;如果他们同时出发,那么
1
小时后两人还相距
11
千米。求张强、李毅每小时各走多少千米?
设张强每小时走
x
千米
李毅每小时走
y
千米
1.某车站有甲、乙两辆汽车,若甲车先出发1h后乙车出发,则乙车出发后5h追上甲车;若甲车先开出20km后乙车出发,则乙车出发4h后追上甲车,求甲乙两车的速度。
巩固训练
2.甲、乙两人在周长为400m的环形跑道上练跑,如果相向出发,每隔2.5min相遇一次;如果同向出发,每隔10min相遇一次,假定两人速度不变,且甲快乙慢,求甲、乙两人的速度.
3、小李骑自行车从A地到B地,小明骑自行车从B地到A地,两人都匀速前进,已知两人在上午8时同时出发,到上午10时,两人还相距36千米,到中午12时,两人又相距36千米,求A,B两地间的路程.
总结
2.追及问题
1.相遇问题
甲的路程+乙的路程=总的路程
快者的路程-慢者的路程=原来相距路程
二.做题技巧
画线段图找等量关系
一.行程问题等量关系
合作探究---列方程组解决行程问题问题
从甲地到乙地有一段上坡与一段平路。如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需54min,从乙地到甲地需42min,甲地到乙地全程是多少?
合作探究---列方程组解决行程问题问题
分析:甲地到乙地的路分成两段,一段为平路,一段为下坡路.
平路:4
m/h
下坡路:5
m/h
上坡路:3
m/h
走平路的时间+走下坡路的时间=________,
走上坡路的时间+走平路的时间=
_______.
42min
54min
合作探究---列方程组解决行程问题问题
平路时间
坡路时间
总时间
甲到乙
乙到甲
解:设甲地到乙地平路长x
m,上坡路长y
m.
根据题意,可列方程组:
解方程组,得
答:甲地到乙地的距离是3.1千米。
所以1.6+1.5=3.1(km)
本题还有其他方法吗?
小试牛刀
1、甲、乙两人相距4km,以各自的速度同时出发.如果同向而行,甲2h追上乙;如果相向而行,两人0.5h后相遇.试问两人的速度各是多少?
分析:对于行程问题,一般可以借助示意图表示题中的数量关系,可以更加直观的找到相等关系.
小试牛刀
(1)
同时出发,同向而行
甲出发点
乙出发点
4km
甲追上乙
乙2h行程
甲2h行程
甲2h行程=4km+乙2h行程
(2)
同时出发,相向而行
甲出发点
乙出发点
4km
相遇地
甲0.5h
行程
乙0.5h
行程
甲0.5h行程+乙0.5h行程=4km
小试牛刀
解:设甲、乙的速度分别为xkm/h,ykm/h.
根据题意,得
解方程组,得
答:甲的速度为5km/h,乙的速度为3km/h.
1.一船顺水航行45千米需要3小时,逆水航行65千米需要5小时,若设船在静水中的速度为x千米/小时,水流的速度为y㎞/h,则x、y的值为
(
)
A、X=3,y=2
B、x=14,y=1
C、x=15,y=1
E、x=14,y=2
B
当堂达标
2.甲、乙二人相距6km,二人同时出发。同向而行,甲3小时可追上乙;相向而行,1小时相遇。二人的平均速度各是多少?
6km
(1)甲3小时行驶路程=乙3小时行驶+6
(2)甲3小时行驶+乙3小时行驶=6
当堂达标
实际问题
数学问题
(二元一次方程组)
解方程组
数学问题的解
(二元一次方程组的解)
双检验
实际问题
的答案
代入法
加减法
(消元)
设未知数、列方程组
利用二元一次方程组分析和解决实际问题的基本过程:
方法归纳
请你说给大家听听
这节课你有哪些收获?
体会.分享
二元一次方程组的应用
应用
步骤
简单实际问题
行程问题
路程=平均速度×时间
审题:弄清题意和题目中的
设元:用_____表示题目中的未知数
列方程组:根据__个等量关系列出方程组
解方程组
检验作答
数量关系
字母
2
代入法;
加减法.
几何问题
?
课堂
小结
谢谢同学们的努力!
