沪科版七年级下册数学10.1.2相交线--垂直教学设计
文档属性
| 名称 | 沪科版七年级下册数学10.1.2相交线--垂直教学设计 |  | |
| 格式 | zip | ||
| 文件大小 | 462.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-26 16:24:43 | ||
图片预览



文档简介
《10.1
.2相交线—垂直》教学设计
一、教学内容解析
上海科学技术出版社义务教育课程标准实验教科书,七年级上册第十章第一节。两条直线的位置关系有三种,相交、平行和异面,异面在高中阶段学习,而相交和平行是同一平面内两条直线的基本位置关系,是“图形与几何”所要研究的基本问题,是初中阶段学习的重点内容之一。
由于两条直线相交的相互位置与它们形成的角有直接关系,所以本节课实际上是研究两条直线相交形成的角的关系,即重点研究对顶角的概念和性质。
在七年级上册,已经学习了最基本的平面图形:直线、射线、线段和角,了解了它们的性质,这是本节课学习的基础,同时本节课的内容对后面的垂线、平行线、三角形、四边形等图形的性质的学习,以及与几何图形有关的推理、计算等问题都有联系,所以本节课内容起着承上启下的作用。
二、教学目标设置:
新课标提出,在课程的学习过程中重视学生的数学活动,发展学生的数感、符号感、空间观念、统计观念,以及应用意识与推理能力。在发展空间观念中提出:能从复杂的图形中分解出基本的图形,并能分析出其中的基本元素及其关系。相交线这节课恰好是构成复杂图形的一个基本图形,是一个起始点,因此通过本节课的学习既要让学生理解对顶角的概念,掌握对顶角的性质,同时要抓住契机,注重能力的培养和思想方法的渗透,并利用活动积累数学活动经验。
基于以上分析,本节课的教学目标确定为:
1、了解邻补角的概念;理解对顶角的概念,能找出图形中的一个角的对顶角;掌握对顶角的性质,会利用对顶角的性质来进行简单的计算和说理;
2、通过“复习角的构成和‘互为补角’的定义,学习邻补角”和“对比邻补角学习对顶角”的过程,让学生感受知识之间的内在联系和几何学习的方法,并在探究过程中体会图形语言、文字语言、符号语言三种语言的相互转换;
3、通过探究对顶角性质,向学生渗透“观察、猜想、操作验证、说理”是得到几何结论的普遍的方法这一道理。
三、学情分析
1、知识的储备:在小学,学生结合生活情境了解平面上两条直线的平行和相交;在七年级上册,学生初步接触简单的平面几何图形,重点研究了线段和角,知道了互余、互补的角,等角的补角(余角)相等等知识,能将生活中的实物抽象成简单的图形,会画简单图形,初步掌握结合图形思考问题,只会极为简单的说理,而且利用余角和补角的性质来进行说理的意识较为淡薄。
2、能力的储备:学生初步具有探究问题的能力,积累了一定的数学活动经验,但对于几何知识的准确表达还存在着困难,尤其是由图形语言、文字语言和符号语言的相互转换,还不能做到准确。
学生已有一定的学习迁移能力,但在图形的性质学习过程中,不会注重图形之间的联系,知识点之间的联系,学习状态是“只见树木,不见森林”,此外学生对获得正确的几何结论的经验和方法还很缺乏。
3、心理特点:七年级学生大都积极、热情,喜欢数学活动和探究,但注意力有时不能集中;七年级学生大都热衷于口头表达,但有条理的书写表达较为困难。
根据上述分析本节课的难点是:对两个过程的理解,即对比邻补角学习的经验,学习对顶角的过程,对顶角性质探索的过程。
为突破难点,做好关键三点:第一,利用知识基础,挖掘知识之间的联系。即利用学生原有的生活经验和知识基础,先明确相交线所形成的角的构成和复习“互为补角”的定义,来学习邻补角,知道邻补角的位置关系决定数量关系。第二,运用对比。即对比邻补角的学习经验,来探究对顶角的位置关系和数量关系,且知道对顶角的位置关系决定数量关系,也从探究过程中理解了对顶角的概念,掌握了对顶角的性质。第三,自主探究,及时鼓励。即在对对顶角性质探索的过程中,设计活动让学生经历实物演示、数学猜想、操作验证和说理证明的过程,让其在合作交流中探索新知、获得新知、感受方法。同时,鼓励学生大胆去说、去写,对能用数学语言有条理的表达给与鼓励和表扬,激发学生逐步探究的信心。第四,利用教育技术资源。结合本节课的内容特点和学生的心理特点,合理使用教育技术资源,让学生更多的参与,更直观的学习,更便捷的互动,从而提高学生的学习兴趣。有效使用教育技术资源,可以增大课堂容量,提高课堂教学的效率。
四、教学过程:
(一)引入
问:什么叫两条直线相交?两条直线相交又可分为几种不同的情况?
垂直是相交线的特殊情况,怎样定义两条直线互相垂直呢?
在相交线的模型(上页练习插图)中,固定木条a,转动木条b。当b的位置变化时,a、b所成的角也会发生变化。当=90°时(图5。1—4),a与b互相垂直。
(二)新课
1、垂直的概念
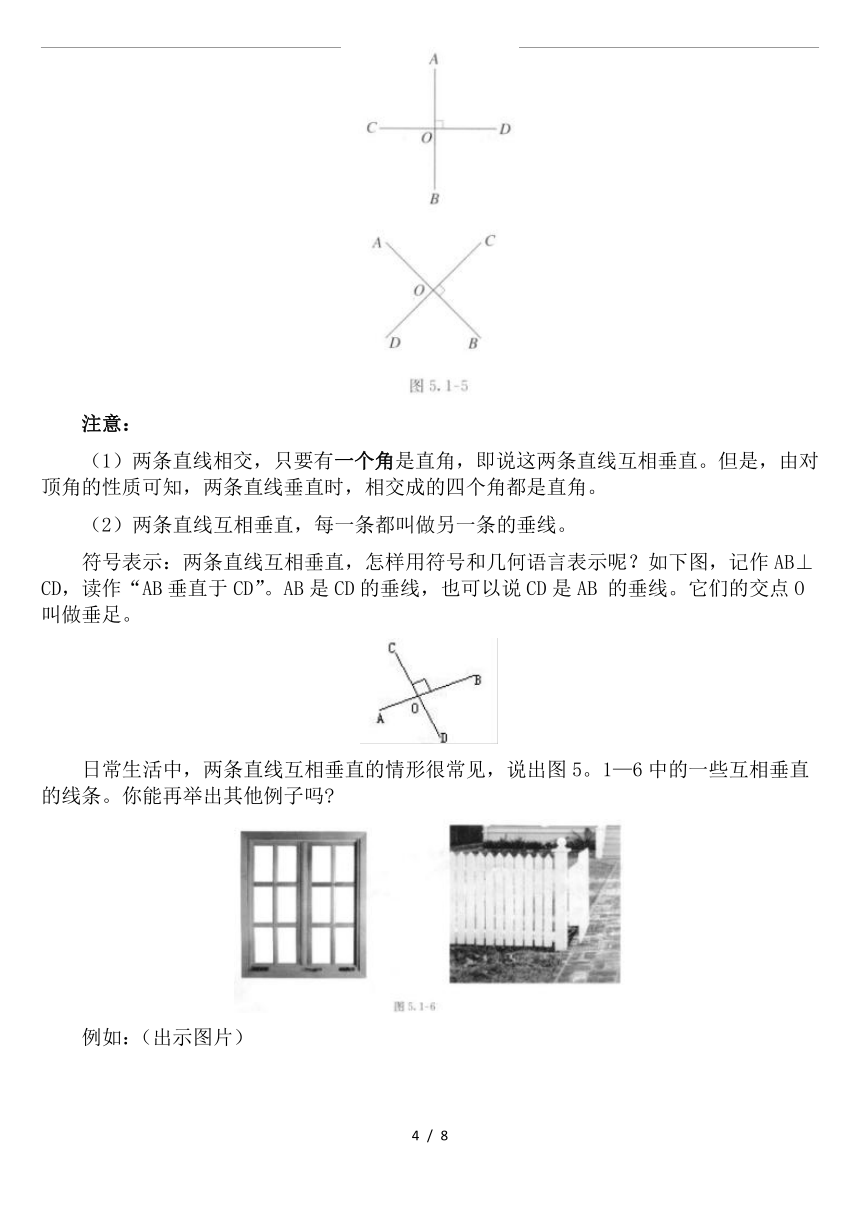
垂直是相交的一种特殊情形,两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足。在图5.1—5中,AB⊥CD,垂足为O。
注意:
(1)两条直线相交,只要有一个角是直角,即说这两条直线互相垂直。但是,由对顶角的性质可知,两条直线垂直时,相交成的四个角都是直角。
(2)两条直线互相垂直,每一条都叫做另一条的垂线。
符号表示:两条直线互相垂直,怎样用符号和几何语言表示呢?如下图,记作AB⊥CD,读作“AB垂直于CD”。AB是CD的垂线,也可以说CD是AB
的垂线。它们的交点O叫做垂足。
日常生活中,两条直线互相垂直的情形很常见,说出图5。1—6中的一些互相垂直的线条。你能再举出其他例子吗?
例如:(出示图片)
请同学们找出图中相互垂直的直线,再举一些生活中的例子。
由于定义既可以当性质用,又可以当判定用,因此可以有以下两个方向的推理过程。
(1)已知垂直关系,可得所成的角为90°(性质)。即:
∵AB⊥CD于O(已知)
∴∠AOD=90°(垂直的定义)
注:写∠AOC=90°、∠COB=90°、∠BOD=90°均可。
(2)已知两直线相交有一个角为90°,可得两直线垂直(判定)。即:
∵∠BOC=90°(已知)
∴AB⊥CD于O(垂直的定义)。
2、垂线的画法
探究1
如图5.1—7。
(1)用三角尺或量角器画已知直线L的垂线,这样的垂线能画出几条?
(2)经过直线L上一点A画L的垂线,这样的垂线能画出几条?
(3)经过直线L外一点B画L的垂线,这样的垂线能画出几条?
垂线的画法:复习小学用三角板过一点A作直线L的垂线的方法,并简记为“靠直线——过定点——画垂线”。
已知直线AB及AB上的一点C,可用如下方法做图:
例1
过线段AB的中点O作线段AB的垂线。
步骤:(1)用刻度尺找到AB的中点O;
(2)用三角板作出过O点且垂直于AB的直线L。
谈一谈:
(1)两条直线相交构成四个角,当其中一个角是直角时,另外三个角是不是直角,为什么?
(2)在一张纸片上画出一条直线AB,你能用折纸的方法画出AB的垂线吗?请说明你是如何折纸的。
3、发现垂线的性质
在学生熟练地作出各条垂线之后,教师继续提问:(或以其它形式)过A点还能作出别的垂线吗?
在学生回答的基础上,教师引导学生发现以下两个结论:
①过A点L的垂线有没有,有。
②过A点作L的垂线有几条,只一条。
在此基础上,又引导学生概括出:垂线的第一个性质公理:过一点有且只有一条直线与已知直线垂直。
注:①“有且只有”中,“有”指“存在”,“只有”指“唯一”。
②“过一点”的点在直线外,或在直线上都可以。
总结:经过一点(已知直线上或直线外),能画出已知直线的一条垂线,并且只能画出一条垂线,即:过一点有且只有一条直线与已知直线垂直。
4、练习
画一条线段或射线的垂线,就是画它们所在直线的垂线。
如图,请你过点P画出线段AB或射线AB的垂线。
思考
在灌溉时,要把河中的水引到农田P处,如何挖渠能使渠道最短?
探究2
如图5.1—9,连接直线L外一点P与直线L上各点
O,
AL,A2,A3,…,其中PO⊥L(我们称PO为点P到直线L的垂线段)。
比较线段PO,PAL,PA2,PA3,…的长短,这些线段中,哪一条最短?
可以让同学们实际测量一下各个线段的长度,从而总结出那条线段最短。
结论:连接直线外一点与直线上各点的所有线段中。垂线段最短。
简单说成:垂线段最短。
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
注意:点到直线的距离是指垂线段的长度,是一个数量,不能说“垂线段是距离”。
现在同学们知道水渠该怎么挖了吗?在图上画出来。
如果图中比例尺为1︰100
000,水渠大约要挖多长?
找一个同学板演,然后订正答案。
(三)小结:
(四)板书设计
相交线(二)垂线概念、性质垂线的画法练习垂线段的概念、性质
PAGE
/
NUMPAGES
.2相交线—垂直》教学设计
一、教学内容解析
上海科学技术出版社义务教育课程标准实验教科书,七年级上册第十章第一节。两条直线的位置关系有三种,相交、平行和异面,异面在高中阶段学习,而相交和平行是同一平面内两条直线的基本位置关系,是“图形与几何”所要研究的基本问题,是初中阶段学习的重点内容之一。
由于两条直线相交的相互位置与它们形成的角有直接关系,所以本节课实际上是研究两条直线相交形成的角的关系,即重点研究对顶角的概念和性质。
在七年级上册,已经学习了最基本的平面图形:直线、射线、线段和角,了解了它们的性质,这是本节课学习的基础,同时本节课的内容对后面的垂线、平行线、三角形、四边形等图形的性质的学习,以及与几何图形有关的推理、计算等问题都有联系,所以本节课内容起着承上启下的作用。
二、教学目标设置:
新课标提出,在课程的学习过程中重视学生的数学活动,发展学生的数感、符号感、空间观念、统计观念,以及应用意识与推理能力。在发展空间观念中提出:能从复杂的图形中分解出基本的图形,并能分析出其中的基本元素及其关系。相交线这节课恰好是构成复杂图形的一个基本图形,是一个起始点,因此通过本节课的学习既要让学生理解对顶角的概念,掌握对顶角的性质,同时要抓住契机,注重能力的培养和思想方法的渗透,并利用活动积累数学活动经验。
基于以上分析,本节课的教学目标确定为:
1、了解邻补角的概念;理解对顶角的概念,能找出图形中的一个角的对顶角;掌握对顶角的性质,会利用对顶角的性质来进行简单的计算和说理;
2、通过“复习角的构成和‘互为补角’的定义,学习邻补角”和“对比邻补角学习对顶角”的过程,让学生感受知识之间的内在联系和几何学习的方法,并在探究过程中体会图形语言、文字语言、符号语言三种语言的相互转换;
3、通过探究对顶角性质,向学生渗透“观察、猜想、操作验证、说理”是得到几何结论的普遍的方法这一道理。
三、学情分析
1、知识的储备:在小学,学生结合生活情境了解平面上两条直线的平行和相交;在七年级上册,学生初步接触简单的平面几何图形,重点研究了线段和角,知道了互余、互补的角,等角的补角(余角)相等等知识,能将生活中的实物抽象成简单的图形,会画简单图形,初步掌握结合图形思考问题,只会极为简单的说理,而且利用余角和补角的性质来进行说理的意识较为淡薄。
2、能力的储备:学生初步具有探究问题的能力,积累了一定的数学活动经验,但对于几何知识的准确表达还存在着困难,尤其是由图形语言、文字语言和符号语言的相互转换,还不能做到准确。
学生已有一定的学习迁移能力,但在图形的性质学习过程中,不会注重图形之间的联系,知识点之间的联系,学习状态是“只见树木,不见森林”,此外学生对获得正确的几何结论的经验和方法还很缺乏。
3、心理特点:七年级学生大都积极、热情,喜欢数学活动和探究,但注意力有时不能集中;七年级学生大都热衷于口头表达,但有条理的书写表达较为困难。
根据上述分析本节课的难点是:对两个过程的理解,即对比邻补角学习的经验,学习对顶角的过程,对顶角性质探索的过程。
为突破难点,做好关键三点:第一,利用知识基础,挖掘知识之间的联系。即利用学生原有的生活经验和知识基础,先明确相交线所形成的角的构成和复习“互为补角”的定义,来学习邻补角,知道邻补角的位置关系决定数量关系。第二,运用对比。即对比邻补角的学习经验,来探究对顶角的位置关系和数量关系,且知道对顶角的位置关系决定数量关系,也从探究过程中理解了对顶角的概念,掌握了对顶角的性质。第三,自主探究,及时鼓励。即在对对顶角性质探索的过程中,设计活动让学生经历实物演示、数学猜想、操作验证和说理证明的过程,让其在合作交流中探索新知、获得新知、感受方法。同时,鼓励学生大胆去说、去写,对能用数学语言有条理的表达给与鼓励和表扬,激发学生逐步探究的信心。第四,利用教育技术资源。结合本节课的内容特点和学生的心理特点,合理使用教育技术资源,让学生更多的参与,更直观的学习,更便捷的互动,从而提高学生的学习兴趣。有效使用教育技术资源,可以增大课堂容量,提高课堂教学的效率。
四、教学过程:
(一)引入
问:什么叫两条直线相交?两条直线相交又可分为几种不同的情况?
垂直是相交线的特殊情况,怎样定义两条直线互相垂直呢?
在相交线的模型(上页练习插图)中,固定木条a,转动木条b。当b的位置变化时,a、b所成的角也会发生变化。当=90°时(图5。1—4),a与b互相垂直。
(二)新课
1、垂直的概念
垂直是相交的一种特殊情形,两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足。在图5.1—5中,AB⊥CD,垂足为O。
注意:
(1)两条直线相交,只要有一个角是直角,即说这两条直线互相垂直。但是,由对顶角的性质可知,两条直线垂直时,相交成的四个角都是直角。
(2)两条直线互相垂直,每一条都叫做另一条的垂线。
符号表示:两条直线互相垂直,怎样用符号和几何语言表示呢?如下图,记作AB⊥CD,读作“AB垂直于CD”。AB是CD的垂线,也可以说CD是AB
的垂线。它们的交点O叫做垂足。
日常生活中,两条直线互相垂直的情形很常见,说出图5。1—6中的一些互相垂直的线条。你能再举出其他例子吗?
例如:(出示图片)
请同学们找出图中相互垂直的直线,再举一些生活中的例子。
由于定义既可以当性质用,又可以当判定用,因此可以有以下两个方向的推理过程。
(1)已知垂直关系,可得所成的角为90°(性质)。即:
∵AB⊥CD于O(已知)
∴∠AOD=90°(垂直的定义)
注:写∠AOC=90°、∠COB=90°、∠BOD=90°均可。
(2)已知两直线相交有一个角为90°,可得两直线垂直(判定)。即:
∵∠BOC=90°(已知)
∴AB⊥CD于O(垂直的定义)。
2、垂线的画法
探究1
如图5.1—7。
(1)用三角尺或量角器画已知直线L的垂线,这样的垂线能画出几条?
(2)经过直线L上一点A画L的垂线,这样的垂线能画出几条?
(3)经过直线L外一点B画L的垂线,这样的垂线能画出几条?
垂线的画法:复习小学用三角板过一点A作直线L的垂线的方法,并简记为“靠直线——过定点——画垂线”。
已知直线AB及AB上的一点C,可用如下方法做图:
例1
过线段AB的中点O作线段AB的垂线。
步骤:(1)用刻度尺找到AB的中点O;
(2)用三角板作出过O点且垂直于AB的直线L。
谈一谈:
(1)两条直线相交构成四个角,当其中一个角是直角时,另外三个角是不是直角,为什么?
(2)在一张纸片上画出一条直线AB,你能用折纸的方法画出AB的垂线吗?请说明你是如何折纸的。
3、发现垂线的性质
在学生熟练地作出各条垂线之后,教师继续提问:(或以其它形式)过A点还能作出别的垂线吗?
在学生回答的基础上,教师引导学生发现以下两个结论:
①过A点L的垂线有没有,有。
②过A点作L的垂线有几条,只一条。
在此基础上,又引导学生概括出:垂线的第一个性质公理:过一点有且只有一条直线与已知直线垂直。
注:①“有且只有”中,“有”指“存在”,“只有”指“唯一”。
②“过一点”的点在直线外,或在直线上都可以。
总结:经过一点(已知直线上或直线外),能画出已知直线的一条垂线,并且只能画出一条垂线,即:过一点有且只有一条直线与已知直线垂直。
4、练习
画一条线段或射线的垂线,就是画它们所在直线的垂线。
如图,请你过点P画出线段AB或射线AB的垂线。
思考
在灌溉时,要把河中的水引到农田P处,如何挖渠能使渠道最短?
探究2
如图5.1—9,连接直线L外一点P与直线L上各点
O,
AL,A2,A3,…,其中PO⊥L(我们称PO为点P到直线L的垂线段)。
比较线段PO,PAL,PA2,PA3,…的长短,这些线段中,哪一条最短?
可以让同学们实际测量一下各个线段的长度,从而总结出那条线段最短。
结论:连接直线外一点与直线上各点的所有线段中。垂线段最短。
简单说成:垂线段最短。
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
注意:点到直线的距离是指垂线段的长度,是一个数量,不能说“垂线段是距离”。
现在同学们知道水渠该怎么挖了吗?在图上画出来。
如果图中比例尺为1︰100
000,水渠大约要挖多长?
找一个同学板演,然后订正答案。
(三)小结:
(四)板书设计
相交线(二)垂线概念、性质垂线的画法练习垂线段的概念、性质
PAGE
/
NUMPAGES
