天津市2020年空中课堂人教版八年级数学下册17.1 勾股定理课件(共29张PPT)
文档属性
| 名称 | 天津市2020年空中课堂人教版八年级数学下册17.1 勾股定理课件(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-26 18:05:01 | ||
图片预览




文档简介
(共29张PPT)
17.1
勾
股
定
理
八年级
数学
1.
探索勾股定理,能运用它解决一些简单的实际问题.
2.
会证明判定直角三角形全等的“斜边、直角边”定理.
3.
能在数轴上作出一些表示无理数的点.
学习目标:
2002
年在北京召开了国际数学家大会,这次大会的会徽,与数学中著名的勾股定理有着密切关系.
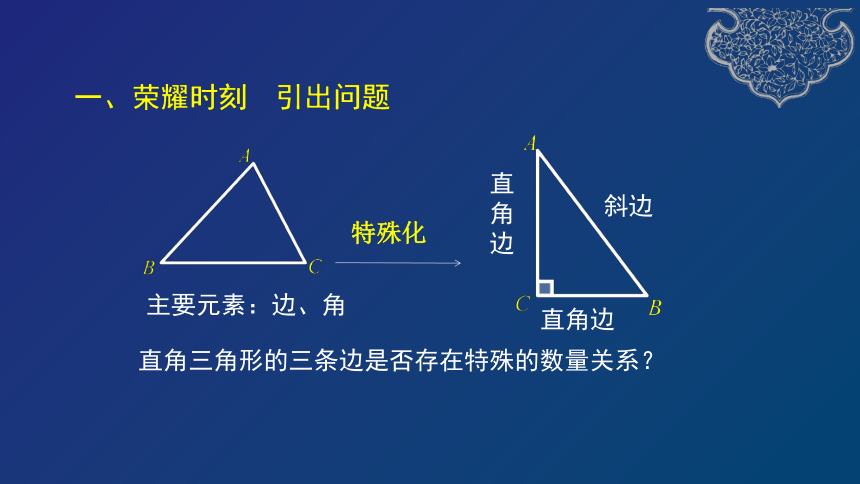
一、荣耀时刻
引出问题
主要元素:边、角
斜边
直角边
直角边
直角三角形的三条边是否存在特殊的数量关系?
特殊化
一、荣耀时刻
引出问题
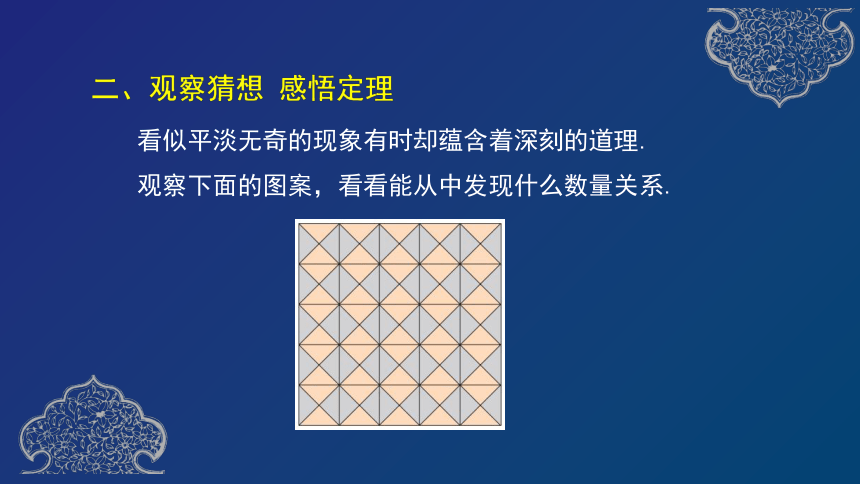
二、观察猜想
感悟定理
看似平淡无奇的现象有时却蕴含着深刻的道理.
观察下面的图案,看看能从中发现什么数量关系.
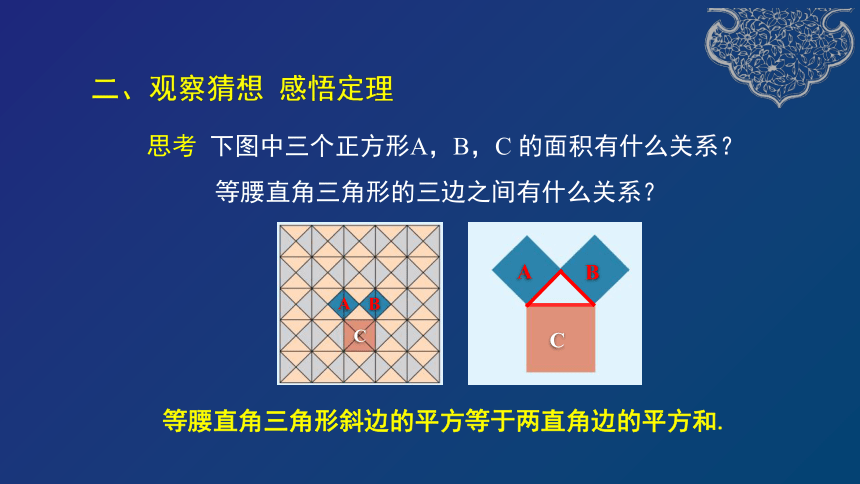
等腰直角三角形斜边的平方等于两直角边的平方和.
思考
下图中三个正方形A,B,C
的面积有什么关系?
二、观察猜想
感悟定理
A
B
C
A
B
C
等腰直角三角形的三边之间有什么关系?
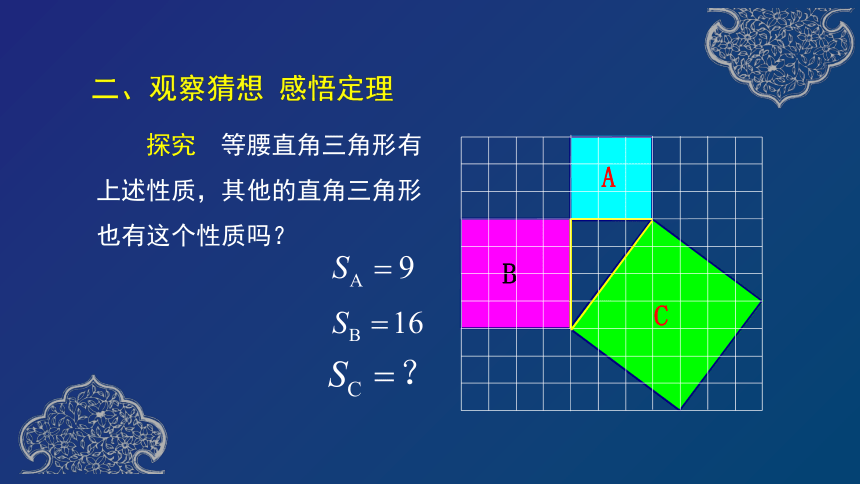
探究
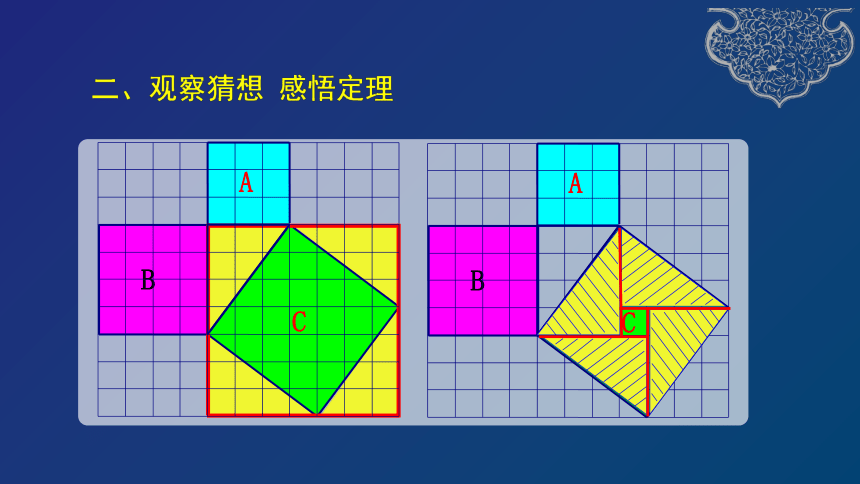
等腰直角三角形有上述性质,其他的直角三角形也有这个性质吗?
A
B
C
二、观察猜想
感悟定理
A
B
C
C
A
B
C
C
二、观察猜想
感悟定理
二、观察猜想
感悟定理
命题1
如果直角三角形的两条直角边长分别为
a,b,
斜边长为
c,那么
a2+b2
=
c2.
在
Rt△ABC
中,若∠C
=
90°,
则
a2+b2
=
c2.
三、动手实践
证明定理
方法1
用面积恒等法证明.
证明:
∵
S大正方形
=
S大正方形
=
=
c2+4
×
ab.
∴
(a+b)2
=
c2+
4×
ab,
a2
+
2ab+b2
=
c2+
2ab,
∴
a2
+
b2
=
c2
.
(a+b)2,
S小正方形+
4
S直角三角形
三、动手实践
证明定理
方法1
用面积恒等法证明.
三、动手实践
证明定理
方法2
用赵爽弦图证明.
三、动手实践
证明定理
方法2
用赵爽弦图证明.
赵爽指出:
按弦图,可以勾股相乘为朱实二,倍之为朱实四.以勾股之差自相乘为中黄实.加差实,亦为弦实.
(b
-a)2
=
c2
4×
ab
+
2ab
+
b2
-
2ab
+a2
=
c2
b2
+a2
=
c2.
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
在△ABC
中,∵∠C
=
90°,
三、动手实践
证明定理
例1
一个门框的尺寸如图所示,一块长
3
m,宽
2.2
m
的长方形薄木板能否从门框内通过?为什么?
四、应用新知
解决问题
分析:
可以看出,木板横着或竖着都不能从门框内通过,只能试试斜着能否通过.门框对角线
AC
的长度是斜着能通过的最大长度.求出
AC,再与木板的宽比较,就能知道木板能否通过.
解:
在Rt△ABC
中,根据勾股定理,
因为
AC
大于木板的宽
2.2
m,所以
木板能从门框内通过.
四、应用新知
解决问题
例2
如图,一架
2.6
m
长的梯子AB
斜靠在一竖直的墙
AO
上,这时
AO
为
2.4
m.如果梯子的顶端
A
沿墙下滑
0.5
m,那么梯子底端
B
也外移
0.5
m
吗?
四、应用新知
解决问题
yuqia:
链接几何画板
解:可以看出,BD
=
OD
-OB.在Rt△AOB
中,根据勾股定理,
四、应用新知
解决问题
在Rt△COD
中,根据勾股定理,
BD
=
OD
-OB
≈
1.77-1=
0.77.
所以梯子的顶端沿墙下滑
0.5
m
时,梯子底端并不是外移
0.5
m,而是外移约
0.77
m.
例3
如图,在
Rt△ABC
和
Rt△A'B'C'
中,∠C=∠C'=90?,
AB=A'B',AC=A'C'.求证:△ABC≌△A'B'C'.
证明:在
Rt
△ABC
和
Rt
△A'B'C'
中,
∠C=∠C'=
90°,根据勾股定理,得
又
AB
=
A'B',AC
=
A'C',
∴
BC
=
B'C'.
∴
△ABC≌△A'B'C'(SSS).
,
五、练习巩固
拓展提高
四、应用新知
解决问题
例4
在数轴上画出表示
的点.
画法:如图,在数轴上找出表示
3
的点
A,则
OA=3,过点
A
作直线
l
垂直于
OA,在
l
上
取点
B,使
AB=2,以原点
O
为圆心,
以
OB
为半径作弧,弧与数轴的交点
C
即为表示
的点.
四、应用新知
解决问题
类似地,利用勾股定理,可以作出长为
,
,
,…的线段.按照同样方法,可以在数轴上画出表示
,
,
,
,
,…的点.
yuqia:
链接无理数的迭代
练习1
在
Rt△ABC
中,∠C
=
90?
,斜边为
c.
①
已知
a
=
5,
b
=
12,求
c.
B
A
C
3
2
B
A
C
12
5
五、练习巩固
拓展提高
解:
在
Rt△
ABC
中,根据勾股定理,
②
已知
b
=
2,c
=
3,求
a.
解:
在
Rt△ABC
中,根据勾股定理,
C
A
B
2
5
练习2
在
Rt△ABC
中,∠B
=
90?,已知
a
=
2,
b
=
5,求
c.
解:
在Rt△
ABC
中,根据勾股定理,
五、练习巩固
拓展提高
五、练习巩固
拓展提高
练习3
在Rt△
ABC
中,∠C
=
90?,∠A
=
30?,AC
=
2,求斜边
AB
的长.
解:
在
Rt△ABC
中,∠C
=
90?,∠A
=
30?,
设
BC
=
x,则AB
=
2x,根据勾股定理,
所以
AB
的长是
练习4
如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形
A,B,C,D
的边长分别是12
,16,9,12,求最大正方形
E
的面积.
五、练习巩固
拓展提高
解:
yuqia:
链接勾股树
六、归纳小结
布置作业
(1)勾股定理的内容是什么?它有什么作用?
(2)对于勾股定理的学习,我们经历了怎样的探索过程?
教材第
28
页习题17.1的第
2,3
题.
六、归纳小结
布置作业
教材第
28
页习题17.1的第
5,6,7
题.
六、归纳小结
布置作业
谢
谢
观
看
!
17.1
勾
股
定
理
八年级
数学
1.
探索勾股定理,能运用它解决一些简单的实际问题.
2.
会证明判定直角三角形全等的“斜边、直角边”定理.
3.
能在数轴上作出一些表示无理数的点.
学习目标:
2002
年在北京召开了国际数学家大会,这次大会的会徽,与数学中著名的勾股定理有着密切关系.
一、荣耀时刻
引出问题
主要元素:边、角
斜边
直角边
直角边
直角三角形的三条边是否存在特殊的数量关系?
特殊化
一、荣耀时刻
引出问题
二、观察猜想
感悟定理
看似平淡无奇的现象有时却蕴含着深刻的道理.
观察下面的图案,看看能从中发现什么数量关系.
等腰直角三角形斜边的平方等于两直角边的平方和.
思考
下图中三个正方形A,B,C
的面积有什么关系?
二、观察猜想
感悟定理
A
B
C
A
B
C
等腰直角三角形的三边之间有什么关系?
探究
等腰直角三角形有上述性质,其他的直角三角形也有这个性质吗?
A
B
C
二、观察猜想
感悟定理
A
B
C
C
A
B
C
C
二、观察猜想
感悟定理
二、观察猜想
感悟定理
命题1
如果直角三角形的两条直角边长分别为
a,b,
斜边长为
c,那么
a2+b2
=
c2.
在
Rt△ABC
中,若∠C
=
90°,
则
a2+b2
=
c2.
三、动手实践
证明定理
方法1
用面积恒等法证明.
证明:
∵
S大正方形
=
S大正方形
=
=
c2+4
×
ab.
∴
(a+b)2
=
c2+
4×
ab,
a2
+
2ab+b2
=
c2+
2ab,
∴
a2
+
b2
=
c2
.
(a+b)2,
S小正方形+
4
S直角三角形
三、动手实践
证明定理
方法1
用面积恒等法证明.
三、动手实践
证明定理
方法2
用赵爽弦图证明.
三、动手实践
证明定理
方法2
用赵爽弦图证明.
赵爽指出:
按弦图,可以勾股相乘为朱实二,倍之为朱实四.以勾股之差自相乘为中黄实.加差实,亦为弦实.
(b
-a)2
=
c2
4×
ab
+
2ab
+
b2
-
2ab
+a2
=
c2
b2
+a2
=
c2.
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
在△ABC
中,∵∠C
=
90°,
三、动手实践
证明定理
例1
一个门框的尺寸如图所示,一块长
3
m,宽
2.2
m
的长方形薄木板能否从门框内通过?为什么?
四、应用新知
解决问题
分析:
可以看出,木板横着或竖着都不能从门框内通过,只能试试斜着能否通过.门框对角线
AC
的长度是斜着能通过的最大长度.求出
AC,再与木板的宽比较,就能知道木板能否通过.
解:
在Rt△ABC
中,根据勾股定理,
因为
AC
大于木板的宽
2.2
m,所以
木板能从门框内通过.
四、应用新知
解决问题
例2
如图,一架
2.6
m
长的梯子AB
斜靠在一竖直的墙
AO
上,这时
AO
为
2.4
m.如果梯子的顶端
A
沿墙下滑
0.5
m,那么梯子底端
B
也外移
0.5
m
吗?
四、应用新知
解决问题
yuqia:
链接几何画板
解:可以看出,BD
=
OD
-OB.在Rt△AOB
中,根据勾股定理,
四、应用新知
解决问题
在Rt△COD
中,根据勾股定理,
BD
=
OD
-OB
≈
1.77-1=
0.77.
所以梯子的顶端沿墙下滑
0.5
m
时,梯子底端并不是外移
0.5
m,而是外移约
0.77
m.
例3
如图,在
Rt△ABC
和
Rt△A'B'C'
中,∠C=∠C'=90?,
AB=A'B',AC=A'C'.求证:△ABC≌△A'B'C'.
证明:在
Rt
△ABC
和
Rt
△A'B'C'
中,
∠C=∠C'=
90°,根据勾股定理,得
又
AB
=
A'B',AC
=
A'C',
∴
BC
=
B'C'.
∴
△ABC≌△A'B'C'(SSS).
,
五、练习巩固
拓展提高
四、应用新知
解决问题
例4
在数轴上画出表示
的点.
画法:如图,在数轴上找出表示
3
的点
A,则
OA=3,过点
A
作直线
l
垂直于
OA,在
l
上
取点
B,使
AB=2,以原点
O
为圆心,
以
OB
为半径作弧,弧与数轴的交点
C
即为表示
的点.
四、应用新知
解决问题
类似地,利用勾股定理,可以作出长为
,
,
,…的线段.按照同样方法,可以在数轴上画出表示
,
,
,
,
,…的点.
yuqia:
链接无理数的迭代
练习1
在
Rt△ABC
中,∠C
=
90?
,斜边为
c.
①
已知
a
=
5,
b
=
12,求
c.
B
A
C
3
2
B
A
C
12
5
五、练习巩固
拓展提高
解:
在
Rt△
ABC
中,根据勾股定理,
②
已知
b
=
2,c
=
3,求
a.
解:
在
Rt△ABC
中,根据勾股定理,
C
A
B
2
5
练习2
在
Rt△ABC
中,∠B
=
90?,已知
a
=
2,
b
=
5,求
c.
解:
在Rt△
ABC
中,根据勾股定理,
五、练习巩固
拓展提高
五、练习巩固
拓展提高
练习3
在Rt△
ABC
中,∠C
=
90?,∠A
=
30?,AC
=
2,求斜边
AB
的长.
解:
在
Rt△ABC
中,∠C
=
90?,∠A
=
30?,
设
BC
=
x,则AB
=
2x,根据勾股定理,
所以
AB
的长是
练习4
如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形
A,B,C,D
的边长分别是12
,16,9,12,求最大正方形
E
的面积.
五、练习巩固
拓展提高
解:
yuqia:
链接勾股树
六、归纳小结
布置作业
(1)勾股定理的内容是什么?它有什么作用?
(2)对于勾股定理的学习,我们经历了怎样的探索过程?
教材第
28
页习题17.1的第
2,3
题.
六、归纳小结
布置作业
教材第
28
页习题17.1的第
5,6,7
题.
六、归纳小结
布置作业
谢
谢
观
看
!
